共计 170646 个字符,预计需要花费 427 分钟才能阅读完成。
《医学统计学》(全本)
第一章 绪论
第一节 医学统计学及其主要内容
医学统计学是运用概率论与数理统计的原理及方法,结合医学实际,研究数字资料的搜集、整理分析与推断的一门学科。
医学研究的对象主要是人体以及与人的健康有关的各种因素。生物现象的一个重要特点就是普遍存在着变异。所谓变异(个体差异),系指相同条件下同类个体之间某一方面发展的不平衡性,系偶然因素起作用的结果。例如同地区、同性别、同年龄的健康人,他们的身长、体重、血压、脉搏、体温、红细胞、白细胞等数值都会有所不同。又如在同样条件下,用同一种药物来治疗某病,有的病人被治愈,有的疗效不显着,有的可能无效甚至死亡。引起客观现象差异的原因是多种多样的,归纳起来,一类原因是普遍的、共同起作用的主要因素,另一类原因则是偶然的、随机起作用的次要因素。这两类原因总是错综复杂地交织在一起,并以某种偶然性的形式表现出来。科学的任务就在于,要从看起来是错综复杂的偶然性中揭露出潜在的必然性,即事物的客观规律性。这种客观规律性是在大量现象中发现的,比如临床要观察某种疗法对某病的疗效时,如果观察的病人很少,便不易正确判断该疗法对某病是否有效;但当观察病人的数量足够多时,就可以得出该疗法在一定程度上有效或无效的结论。所以,医学统计学是医学科学研究的重要工具。
医学统计学在本世纪二十年代以后才逐渐形成为一门学科。解放前,我国学者即致力于把统计方法应用到医学中去,但人力有限、范围较窄。解放后,随着医学科研工作的发展,本学科得到迅速普及与提高。通过大量实践,在不少方面积累了自己的经验,丰富了医学统计学的内容。而电子计算机的作用,更促进了多变量分析等统计方法在医学研究中的应用。
医学统计学的内容包括:①统计研究设计。我们制订调查计划或实验设计时,除专业问题外,还必须从医学统计学的角度考虑,使调查或实验结果能够科学地回答所研究的问题。一个好的设计可以用较少的人力、物力和时间取得更多的较可靠的资料。②总体指标的估计。医学研究中实际观测或调查的部分个体称为样本,研究对象的全体称为总体。人们除用均数、率等统计指标对调查或实验结果进行描述外,更重要的是通过样本的信息,来估计总体中相应的统计指标,即参数估计。③假设检验。就是依据资料性质和所需解决的问题,先建立适当的假设,然后采用适当的检验方法,根据样本是否支持所作的假设,来决定对假设的接受或拒绝。④联系、分类、鉴别与鉴测等研究。在疾病的防治工作中,经常要探讨各种现象数量间的联系,寻找与某病关系最密切的因素;要进行多种检查结果的综合评定、探讨疾病的分型分类:计量诊断,选择治疗方案;要对某些疾病进行预测预报、流行病学监督,对药品制造、临床化验工作等作质量控制,以及医学人口学研究等。医学统计学,特别是其中的多变量分析,为解决这些问题提供了必要的方法和手段。本讲义介绍了医学统计的基本内容,此外,本讲义中还包括军医必须了解或掌握的我军部队、医院、战时的各种登记和统计表,常用统计指标的计算和分析等内容。
作为医学科学工作者,学习和掌握一定的统计学知识是十分必要的。第一,在阅读医学书刊中,经常会遇到一些统计学方面的名词概念,有了这方面的知识,有助于正确理解文章的涵义;第二,军医在实际工作中,经常要做登记工作,要填写各种报表,只有懂得了原始登记与统计结果的密切关系,并掌握了收集、整理与分析资料的基本知识与技能,才能自觉地、认真地把登记工作做好,积累有科学价值的资料;第三,参加科研工作时,从开始设计到数据整理分析与统计结果的表达,每一步骤都需要统计学知识;第四,在制订计划、检查工作、总结经验时,都离不开统计数字,尤其在撰写科研论文时,有了统计学知识,才能使数据与观点密切结合,作出正确的结论。
医务工作者学习统计学,首先必须明确:我们应该掌握的关键不是数学原理,而是怎样合理地、恰当地把数理统计的方法应用到医学科研工作中去,并结合专业知识,提高分析问题与解决问题的能力。其次在学习过程中,要理论联系实际,重视实习与练习。作业中要遵守数学上的规则与习惯,如小数点及各个位数应上下对齐,一个多位数的数值不能分写成两行,等号不能写在一行的末了而应写在第二行的开头等等。再次,各种统计符号必须写正确,汉字、阿拉伯字与外文字母必须写清楚,不能写成模棱两可,只有在学习时养成良好的习惯,将来工作中才能少出差错。
最后我们着重指出:统计工作最根本的一条就是实事求是,如实反映情况。因此,无论日常工作或科学研究中,必须养成严肃认真的作风和反复核对的习惯,同一切弄虚作假的现象进行坚决的斗争,尽最大努力获得正确数据,使分析结论建立在可靠的基础上。
第二节 医学统计学常用的名词概念
一、样本与总体
前面已提及,医学研究中实际观测或调查的一部分个体称为样本,研究对象的全部称为总体。如作水质检验时从井水或河水中采的水样,临床化验中从病人身上采的血液或其它活体组织标本,是样本;而整个一口井或一条河的某一段所有的水,某病人全身所有的血液或某个组织器官,则是总体。这类总体是具体存在的,但另有些总体却是假想的,只是理论上存在的一个范围。例如试验某一治疗流感新药的疗效,最初接受治疗的一批流感患者,不论数量多少,都只是一个样本。若该药疗效得到肯定,从而加以推广,那么此后凡在相同条件下接受该药治疗的所有流感患者,都属于这个总体。可是当初试用时,这个总体还并不存在,是假想的。
总体包含的观察单位通常是大量的甚至是无限的,在实际工作中,一般不可能或不必要对每个观察单位逐一进行研究。我们只能从中抽取一部分观察单位加以实际观察或调查研究,根据对这一部分观察单位的观察研究结果,再去推论和估计总体情况。如上述某新药治疗流感例子,试验治疗的只是少数有限的病人,而结论却要推广到全体,得出一个该药对所有流感患者之疗效的规律性的认识。所以说,观察样本的目的在于推论总体,这就是样本与总体的辩证关系。
为了使样本能够正确反映总体情况,对总体要有明确的规定;总体内所有观察单位必须是同质的;在抽取样本的过程中,必须遵守随机化原则;样本的观察单位还要有足够的数量。
二、概率
又称机率,是用以描述某事件发生的可能性大小的一个数值。
在自然界和人类社会中,存在着两类不同的现象:①在一定条件下,肯定发生的事件叫做必然事件,肯定不发生的事件叫做不可能事件。如在适当温度湿度下经一定时间孵化,正常受精鸡蛋必然会孵出小鸡来,而石头是不可能孵出小鸡来的。必然事件与不可能事件虽然形式相反,但两者在发生某种结果与否都是确定的,故统称确定性现象。②在基本条件不变的情况下,可能发生的结果有多种,究竟发生哪种结果,事先不能肯定,这类现象叫做随机现象。随机现象的表现结果称为随机事件。如任意抛掷一枚硬币,可能徽花向上也可能币值向上,抛掷前不能肯定,这是一个随机现象,而结果出现“徵花向上”则是一个随机事件。
(一)古典概率 是最简单的随机现象的概率计算。这类随机现象具有两个特征:①在观察或试验中它的全部可能结果只有有限个,譬如为 n 个,记为 E 1,E2,…,En,而且这些事件是两两互不相容的,即任何两个事件不能同时发生;②事件 E 1,E2,…,En的发生或出现是等可能的,即它们发生的概率都一样。古典概率的大部分问题都能形象地用摸球模型来描述。有利于直观地理解概率论的许多基本概念;而且它有着多方面的重要应用,例如工业产品的抽样检查等。
(二)统计概率 上述“事件”是指不能再进行分解或不能由其它事件构成的基本事件。在实际工作中,基本事件的发生并不总是等可能的,而且有时为无穷多个。这样就有必要把古典概率的定义加以推广,从事后经验的角度来理解概率的意义。实践证明,虽然个别随机事件在某次试验或观察中可以出现也可以不出现,但在大量重复试验中它却呈现出明显的规律性。假设在相同条件下,独立地重复做 n 次试验,某随机事件 A 在 n 次试验中出现了 m 次,则比值 m / n 称为随机事件 A 在 n 次试验中出现的频率。当试验重复很多次时,随机事件 A 的频率 m / n 就会在某个固定的常数 P 附近摆动,而且 n 愈大摆动的幅度愈小。这种规律性称之为统计规律性。频率的稳定性说明随机事件发生的可能性大小是随机事件本身固有的、不随人们意志为转移的客观属性,所以在医学科研中,当 n 充分大时,就以频率作为概率的近似值,记住 P(A)即
![]()
由此可见,频率是就样本而言的,而概率总是从总体的意义上说的。这样,概率就为预计某一事件发生的可能性大小,提供了衡量的尺度。
例如:某病患者 40 名,用某疗法治疗后,其中 35 人痊愈,治愈者占治疗人数的 35/40,这是频率。因为数量少,这个频率可能波动较大。假如经过长期的大量观察,比如数百、数千例,得到治愈率为 70%,我们就可以说,该疗法治愈某病的概率近似值为 70%。
又如:某院妇产科在一个月内出生婴儿 30 名,其中男婴 18 名,占新生儿数的 18/30,这叫频率。大量统计表明,人口中男女的比例基本上是 1:1。这是个较稳定的常数,即概率的近似值。于是,在婴儿分娩前,我们就可用它作为尺度,预计是男的概率为 1 /2(0.5 或 50%),是女的概率也为 1 /2(0.5 或 50%)。
通过以上讨论,可以知道:如果某事件是必然事件,则有 m =n,所以必然事件的概率等于 1;如果某事件是不可能事件,则有 m =0,所以不可能事件的概率等于 0;如果某事件是随机事件,则有 0 <m<n,所以随机事件的概率是介于 0 与 1 之间的一个数。某事件的概率愈接近 0,表示发生的可能性愈小;愈接受 1,表示发生的可能性愈大。< p=””></m<n,所以随机事件的概率是介于 0 与 1 之间的一个数。某事件的概率愈接近 0,表示发生的可能性愈小;愈接受 1,表示发生的可能性愈大。<>
三、随机变量
简单地说,是指随机事件的数量表现。例如一批注入某种毒物的动物,在一定时间内死亡的只数;某地若干名男性健康成人中,每人血红蛋白量的测定值;等等。另有一些现象并不直接表现为数量,例如人口的男女性别、试验结果的阳性或阴性等,但我们可以规定男性为 1,女性为 0,则非数量标志也可以用数量来表示。这些例子中所提到的量,尽管它们的具体内容是各式各样的,但从数学观点来看,它们表现了同一种情况,这就是每个变量都可以随机地取得不同的数值,而在进行试验或测量之前,我们要预言这个变量将取得某个确定的数值是不可能的。
按照随机变量可能取得的值,可以把它们分为两种基本类型:①离散型随机变量,即在一定区间内变量取值为有限个,或数值可以一一列举出来。例如某地区某年人口的出生数、死亡数,某药治疗某病病人的有效数、无效数等。②连续型随机变量,即在一定区间内变量取值有无限人, 或数值无法一一列举出来。例如某地区男性健康成人的身长值、体重值,一批传染性肝炎患者的血清转氨酶测定值等。
四、误差
误差是指实际观察值与客观真值之差、样本指标与总体指标之差。误差可分为系统误差和随机误差。
(一)系统误差 在实际观测过程中,由于仪器未校正、测量者感官的某种障碍、医生掌握疗效标准偏高或偏低等原因,使观察值不是分散在真值两侧,而是有方向性、系统性或周期性地偏离真值。这类误差可以通过实验设计和技术措施来消除或使之减弱,但不能靠概率统计办法来消除或减弱。
(二)随机误差 或称偶然误差,是指排除了系统误差后尚存的误差。它受多种因素的影响,使观察值不按方向性和系统性而随机地变化。随机误差服从正态分布,可以用概率统计方法处理。
在随机误差中,最重要的是抽样误差。我们从同一总体中随机抽取若干个大小相同的样本,各样本平均数(或率)之间会有所不同。这些样本间的差异,同时反映了样本与总体间的差异。它是由于从总体中抽取样本才出现的误差,统计上称为抽样误差(或抽样波动)。抽样误差在医学生物实验中最主要的来源是个体的变异。所以这是一种难以控制的、不可避免的误差。但抽样误差是有一定规律的。研究和运用抽样误差的规律, 是根据样本估计总体时所必须领会的基本概念之一,也是医学统计学的重要内容之一。
随机误差中还包括重复误差。它是由于对同一受试对象或检样采用同一方法重复测定时所出现的误差。如用天平称同一个烧杯的重量,重复测定多次,其结果会有某些波动。控制重复误差的手段主要是改进测定方法,提高操作者的熟练程度。重复是摸清实验误差大小的手段,以便分析和减少实验误差。
五、假设检验
亦称显着性检验,其基本原理是先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作出推断。
生物现象的个体差异是客观存在,以致抽样误差不可避免,所以我们不能仅凭个别样本的值来下结论。当遇到两个或几个样本均数(或率)、样本均数(率)与已知总体均数(率)有大有小时,应当考虑到造成这种差别的原因有两种可能:一是这两个或几个样本均数(或率)来自同一总体,其差别仅仅由于抽样误差即偶然性所造成;二是这两个或几个样本均数(或率)来自不同的总体,即其差别不仅由抽样误差造成,而主要是由实验因素不同所引起的。假设检验的目的就在于排除抽样误差的影响,区分差别在统计上是否成立,并了解事件发生的概率。
进行假设检验时,要先建立检验假设(即上述第一种可能,符号是 H)与备择假设(即上述第二种可能,符号是 H 1),确立检验水准(当检验假设为真,但被错误地拒绝的概率,记作 α),通常取 α =0.05 或 α =0.01;然后由样本观察值按相应的公式计算统计量,如 X 2值、t 值等;最后查有关的统计用表确定 P 值范围(有时也可直接计算 P 值)作出结论。若 P >α,结论为按 α 所取水准不显著,不拒绝 H,即认为差别很可能是由于抽样误差造成的,在统计上不成立;如果 P≤α, 结论为按所取 α 水准显著,拒绝 H,接受 H 1,则认为此差别不大可能仅由抽样误差所致, 很可能是实验因素不同造成的,故在统计上成立。
第三节 计数资料与计量资料
医学统计资料按其性质一般分为计数资料与计量资料两类。不同类型的统计资料应采用不同的统计分析方法。
计数资料是先将观察单位按某种属性或类别分成若干组,再清点各组观察单位个数所得到的资料。如临床某些检验结果用阳性或阴性反应表示,对一批某病患者检验完毕后,清点呈阳性或阴性反应的各有若干例。又如要调查某人群的血型分布,先按 A、B、AB、O 四型分组,再清点各血型组人数。计数资料每个观察单位之间没有量的差别,但各组之间具有质的不同,不同性质的观察单位不能归入一组。对这类资料通常是先计算百分比或率等相对数,需要时做百分比或率之间的比较,也可做两事物之间相关的相关分析。
计量资料是用仪器、工具或其它定量方法对每个观察单位的某项标志进行测量,并把测量结果用数值大小表示出来的资料,一般带有度量衡或其它单位。如检查一批应征青年体重,需要磅秤测量,通常以公斤为单位,测得许多大小不一的体重值。其它如身长(cm)、血压(mmHg)、脉搏(次/分)、红细胞(万 /mm3)转氨酶(单位)等,都属于计量资料。每个观察单位的观测值之间有量的区别,但同一批观察单位必须是同质的。对这类资料通常先计算平均数与标准差等指标,需要时做各均数之间的比较或各变量之间的分析。
还有一些资料,也是将观察单位按某种属性或某个标志分组,然后清点各组观察单位个数得来的,但所分各组之间具有等级顺序。这些资料既具有计数资料的特点,又兼有半定量的性质,称为等级资料或半定量资料。例如对一批急性病毒性肝炎患者作麝香草酚絮状试验,将试验结果按 -、+、++、+++、++++ 分组,显然各组之间既有等级顺序,又有程序与量的差别。又如某病住院病人的治疗结果,按治愈、好转、无效、死亡分组,同样各组之间具有顺序与程度之别。分析等级资料常用的统计指标有比和率,常用的统计方法有秩和检验、参照单位分析等。
在医学实践中,根据分析研究的目的,计数资料与计量资料可以互相转化。例如血压值本是计量资料,但如果将一组 20-40 岁成年人的血压值分为血压正常与血压异常两组,再清点各组人数,于是这组血压资料就转化成为计数资料了。假若将这组血压值按低血压(<80/60 毫米汞柱)、正常血压(80-130/60-89 毫米汞柱)、轻中度高血压(>130/90-110 毫米汞柱)、重度高血压(>130/>110 毫米汞柱)的等级顺序分组,清点各组人数,这时这组血压资料又转化为等级资料了。又如在计量诊断中,将某些阳性体征根据确诊病人的概率赋予分数,分数的多少代表量的大小,这样原来的计数资料就转化为计量资料。
由于计量资料可以得到较多的信息,所以凡能计量的,尽量采用计量资料。
第二章 统计表与统计图
统计表与统计图是整理、表达和分析数字资料的重要工具。运用统计表可避免冗长的方案叙述。能把有关的数字列在一起,既便于计算比较,又易于发现错误和遗漏。绘制统计图可使数字资料形象化、通俗易懂,并能把资料的变化趋势和各种现象间的关系明确地表示再现,使读者在短时间内获得明晰的印象。统计图只能表示概数,要想了解准确的数字,仍需看统计表。
第一节 统计表
统计表可从广义或狭义上看。广义的统计表包括调查表、登记表、过渡表及表达最后结果的统计表在内。狭义的统计表是指表达统计结果的统计表。下面简述狭义统计表的结构和编制。
一、统计表的构成
从统计表的外形看,可分为标题、标目、线条和数字等;从表的内容上看,又可分为主辞和宾辞两部分。统计表中被说明的事物称为表的主辞,用来说明主辞的统计指标称为表的宾辞,统计表的基本格式如下:
表号标题(包括何时、何地、何事)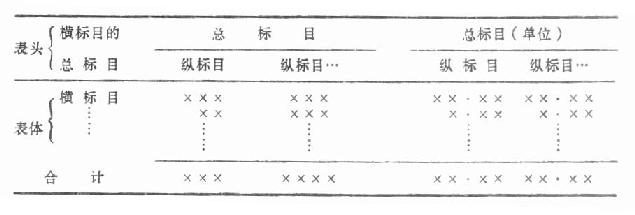
备注:
例如:表 2.1 是某医院用五种检查方法,对上消化道恶性肿瘤的检出率。其中五种检查方法是统计表的主辞,放在表的左侧横标目位置:而检查数、检出数和检出率是统计指标,为宾辞,放在表的右侧,即纵标目位置。一张设计比较好的统计表,将主辞和宾辞结合起来,可读成一句完整而通顺的话。如:胃镜检查 48 例,检出 44 例,检出率为 91.7% 等。
表 2.1 各种方法对上消化道恶性肿瘤检出率
| 检查方法 | 检查数 | 检出数 | 检出率(%) |
| 胃镜 | 48 | 44 | 91.7 |
| 病理活检 | 48 | 34 | 70.8 |
| 钡餐 | 35 | 14 | 40.0 |
| 刷子细胞 | 16 | 10 | 62.5 |
| 联合诊断 | 16 | 16 | 100.0 |
应注意,在编制统计表时,一般都将主辞置于表的左侧,宾辞置于表的右侧。但有时为了节省篇幅或便于排印,而把主辞和宾辞的位置互换,如表 2.6。因此,阅读统计表时,应从内容上而不要只从位置上来辨别主辞与宾辞。
二、统计表的种类
根据主辞的情况,统计表可分为三种:简单表、分组表和复合表。
(一)简单表 主辞未经任何分组,只罗列了观察单位(或地区)、时间或统计指标的统计表,称为简单表。如表 2.1 只罗列了检查方法,故为简单表。
(二)分组表 主辞按一个标志分组的统计表称为分组表。如表 2.2 出院病人只按治疗结果一个标志分了组,故为分组表。
表 2.2 某医院出院病人的治疗结果,1977 年
| 治疗结果 | 出院人数 | 占出院总人数百分比(%) |
| 治 愈 | 3,795 | 80.1 |
| 好 转 | 676 | 14.2 |
| 无变化 | 206 | 4.3 |
| 转他院 | 18 | 0.4 |
| 死 亡 | 50 | 1.0 |
| 合 计 | 4,745 | 100.0 |
(三)复合表 主辞按两个或两个以上标志结合起来分组的统计表称为复合表。如:表 2.3 是将心绞痛病人按病情严重程度及疗效结合起来分组的,故为复合表。
表 2.3 某医院用“725—1”治疗心绞痛病人的疗效,1975 年
| 病 情 | 显效 | 改善 | 无改变 | 合计 |
| 轻 度 | 17 | 24 | 3 | 44 |
| 中 度 | 10 | 19 | 4 | 33 |
| 较重度 | 2 | — | 1 | 3 |
| 总 计 | 29 | 43 | 8 | 80 |
三、编制统计表的注意事项
(一)内容 要简单明了,不可包罗万象。通常一个表只表达一个或两个内容。
(二)主辞与宾辞 要划分清楚。通常主辞置于表的左侧,宾辞在右侧(有时为了节省篇幅,主辞与宾辞的位置也可互换)。
(三)标题 是统计表的总名称,要用一句简单而又确切的话写出。通常包括表所说明的中心内容及时间和地点。
(四)标目 统计表的标目有三种;纵标目、横标目和总标目。纵标目位于表的上端,说明该纵栏指标的含义及度量单位;横标目位于表的左侧,说明该横栏数字的含义;几个纵标目或横标目具有共同性质时,可冠以总标目。标目处理得好坏,是决定统计表质量的关键之一,因此,在制表中必须充分利用纵横两上标目,妥善安排主辞与宾辞的位置,此外,标目的层次不宜太多,(通常 1 至 2 层,最多不宜超过 3 层)。
(五)数字 表内的数字是统计表的基本语言,必须准确无误。要求同一种统计指标各数值的准确度一致,书写时要求各个位数或小数点要上下对齐。表中数字暂缺时用“…”号填充。
(六)线条 统计表中的线条应尽量少,但构成表的基本线条不能缺。通常表的上下边线,表头与表体之间,表头内总标目与纵标目之间都应有横线;如有合计时,部份数字与合计数字之间也要用横线隔开,其它线条均可省略。
(七)备注 备注不是统计表的必需组成部分,遇有特殊情况须用备注时,可写在表的下面。
四、不良统计表的修改举例
表 2.4 是某医院传染科用侧柏叶注射液合并化疗(简称合并组)与单纯化疗(简称化疗组)两种疗法各治疗肺结核 34 例的疗效比较。该表绘制时存在以下缺点:(1)表的左上角不应有斜线,左上角标目与表内重复,应删去。(2)纵标目重复太多,(3)格线太多。(4)平均日数字精确度不一致,修改后见表 2.5。
表 2.4 两组病例主要症状及体征恢复正常所需平均日数
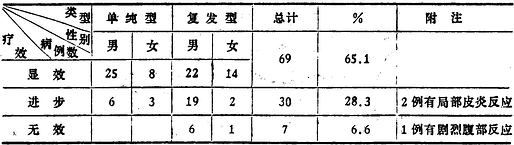
表 2.5 两组病例 (各 34 例) 主要症状与体征恢复正常平均日数
| 症状与体征 | 例 数 | 恢复正常的平均日数 | |||
| 化疗组 | 合并组 | 化疗组 | 合并组 | 相差 | |
| 咳嗽咳痰 | 13 | 17 | 37.7 | 25.7 | 12.0 |
| 嘲热 | 8 | 11 | 40.0 | 26.6 | 13.4 |
| 肺部湿罗音 | 7 | 9 | 63.1 | 30.1 | 33.0 |
| 血沉大于 20 毫米 | 12 | 15 | 77.9 | 47.0 | 30.9 |
| 痰结核菌阳性 | 4 | 7 | 133.2 | 82.0 | 51.2 |
第二节 统计图
统计表的资料用几何图形或图案等形式表示即成为统计图。
一、统计图的种类与构造
统计图种类很多,常用的有:条图、圆图、百分条图、线图(包括半对数线图)、直方图和统计地图等。
统计图由以下各部份构成:
(一)标题 每个图都应有标题。标题要简明确切,通常包括内容、时间和地点。其位置在图域之外,一般放在图域的下面。
(二)图域 图域的长宽之比一般 7:5 为美观,圆图除外。
(三)标目 纵横两轴应有标目,即纵标目和横标目,并注明度量衡单位。
(四)尺度 纵横两轴都有尺度,横轴尺度自左至右,纵轴尺度自下而上,数值一律由小而大。尺度间隔要宽松。用算术尺度时,等长的距离应代表相等的数量。
(五)图例 用不同线条或颜色代表不同事物时,需用图例说明。
二、资料性质与图形选择
统计资料的性质决定于统计表的主辞。主辞可分为品质的和数量的两类。主辞是品质的,如单位名称、性别、病型等为品质资料;主辞为数量的,如年龄、时间、脉搏等称为数量资料。数量资料又可分为连续性资料和间断性资料。连续性资料是指任何两个小的数值之间可以有无限个数值存在,如时间可依次分为年、月、日、时、分、秒、十分之一秒……等,所以时间是连续性资料。至于家庭人口数,在原始记录上不可能找到有 4.3 或 5.8 人口的家庭,所以人口数是间断性资料。
各类资料宜用何种图形表达示意如下:

三、常用统计图的绘制方法及注意事项
(一)条图 又名长条图,以条的长度表示事物的数量。可用以表示绝对数、也可用以表示相对数或平均数,常用的有单式条图、复式条图和分段条图。
1.单式条图:如图 2.1,为某医院十年来六种疾病住院患者死亡人数。其资料见表 2.6。
2.复式条图:用以比较两种或两种以上有关事物的数量。如图 2.2 表示某师各团菌痢和肠炎的发病人数,其资料见表 2.7。
3.分段条图:用以比较事物的全部与其中一部分的数量。如图 2.3 表示某师各团传染病总人数及菌痢人数,其资料见表 2.8。
绘制条图时应注意以下各点:
(1)图中各条要有同一基线,其尺度必须从“0”开始,否则会改变条间的比例关系。
(2)条的排列顺序由高到低,如事物有自然顺序者,也可按自然顺序排列。
(3)各条的宽度要一致,条间的空隙要相等,条间空隙一般不要大于条宽。
(4)尽量避免用折断或回转的条。
表 2.6 某医院十年来六种疾病住院患者死亡人数
| 病名 | 瘤(癌) | 脑外伤 | 心脏病 | 白血病 | 脑溢血 | 肺炎 |
| 死亡人数 | 187 | 44 | 42 | 38 | 32 | 29 |
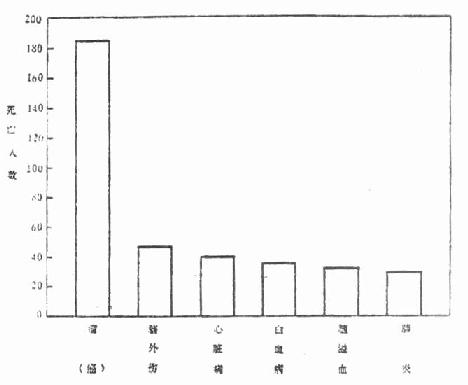
图 2.1 某医院十年来六种疾病住院患者死亡人数
表 2.7 某师各团菌痢、肠炎发病人数 19××年
| 病种 | 一团 | 二团 | 三团 | 炮团 |
| 菌痢 | 41 | 43 | 61 | 34 |
| 肠炎 | 26 | 23 | 38 | 35 |
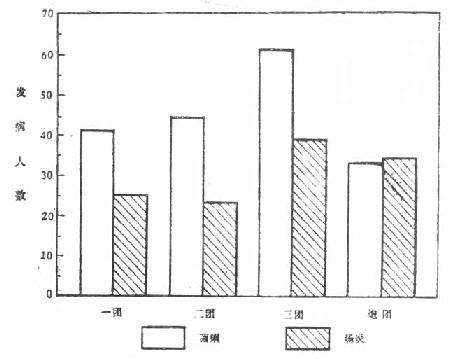
图 2.2 某师各团菌痢、肠炎发病人数(19××年)
表 2.8 某师各团传染病部人数及菌痢发病人数 19××年
| 一团 | 二团 | 三团 | 炮团 | |
| 传染病发病总人数 | 81 | 148 | 179 | 128 |
| 其中菌痢发病人数 | 41 | 43 | 61 | 34 |
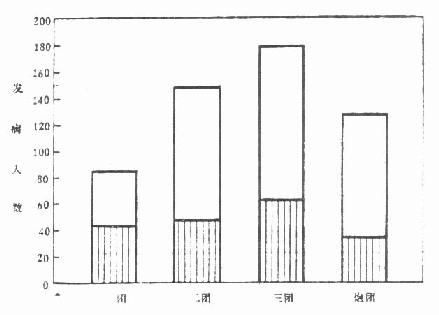
图 2.3 某师各团传染病总人数及菌痢发病人数(长条全段表示传染病发病人数,下段表示菌痢发病人数)
(二)圆图 圆图用扇形的面积,也就是圆心角的度数来表示数量。它用来表示组数不多的品质资料或间断性数量资料的内部构成,各部份百分比之各和必须是 100%。如图 2.4 表示某医院用 10% 明矾液治疗面部深层海绵状血管瘤的疗效构成,其资料见表 2.9。
圆心角(度)的计算方法是将百分数乘以 360,如表 2.9 中的特效百分比所占的圆心角度数为 69.5%×360=250.2, 余类推,见表 2.9 最后一栏。
绘制圆图时应注意:各扇形应按大小或自然顺序自时钟 9 时或 12 时处开始,顺时针方向排列;各扇形内要注明简要的文字和百分比。
表 2.9 10% 明矾液治疗面部深层海棉状血管瘤疗效
| 疗效 | 病例数 | 百分比(%) | 绘图用圆心角(度) |
| 特效 | 66 | 69.7 | 250.0 |
| 显效 | 14 | 14.7 | 52.9 |
| 有效 | 11 | 11.6 | 41.8 |
| 无效 | 4 | 4.2 | 15.1 |
| 合计 | 95 | 100.0 | 360.0 |
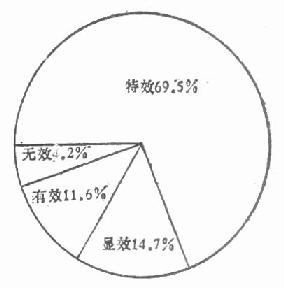
图 2 -4 10% 明矾治疗面部深层海绵状血管瘤疗效
(三)百分条图 凡能画圆图的资料,也可用百分条图表示,绘制方便。尤其在比较几个组的内部构成时,可绘制长宽相同的几个直径,各直条内相应构成部分的排列顺序、花纹或图案应一致,并附一百分尺度。如图 2 -5,资料来源见表 2 -10。
表 2 -10 某医院用脊电针治疗慢性支气管炎的结果 19××年
| 病型 | 总例数 | 人 数 | 百分比(%) | ||||||
| 近控 | 显效 | 好转 | 无效 | 近控 | 显效 | 好转 | 无效 | ||
| 单纯型 | 834 | 525 | 180 | 103 | 26 | 62.9 | 21.6 | 12.4 | 3.1 |
| 喘息型 | 179 | 93 | 38 | 34 | 14 | 52.0 | 21.2 | 19.0 | 7.8 |
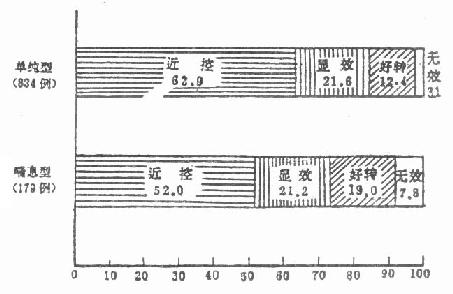
图 2 -5 某医院用脊电针治疗慢性支气管炎的结果
(四)线图 线图适用于连续性数量资料,常用以表示事物或现象在时间上的发展变化,如图 2 -6。从图中可看出 7~10 月份为菌痢发病的高峰期。资料见表 2 -11。
绘制线图时,通常以横轴表示时间或变量,纵轴表示指标,两轴的尺度均可不从“0”点开始。图内线条一般不超过四、五条,可分别以不同的线段或颜色表示,并附图例说明。
表 2 -11 某部队 1970 年逐月菌痢发病人数
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 合计 |
| 发病人数 | 4 | 4 | 6 | 5 | 7 | 8 | 28 | 75 | 97 | 49 | 27 | 14 | 324 |
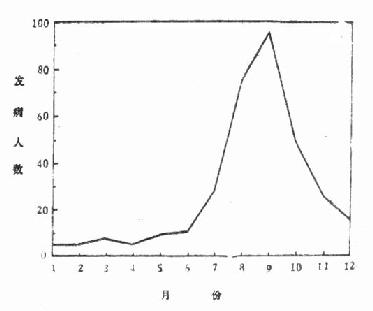
图 2 -6 某部队 1970 年逐月菌痢发病人数
半对数线图 用于比较两种或两种以上率的变化速度。它是将线图绘在半对数坐标纸(纵轴为对数尺度,横轴为算术尺度)上。如果将表 2 -12 中的三组数据时间从 A 到 B 分别绘在算术格纸(图 2 -7)与半对数格纸(图 2 -8)上,将呈现两种不同的结果。
表 2 -12 绝对差与相对差比较
| A→B | 绝对差(A-B) | 相对比(A/B) | 对数差(1gA-1gB) |
| (1)1000→100 | 1000-100=900 | 1000/100=10 | 1g 1000 -1g 100=3-2=1 |
| (2)100→10 | 100-10=90 | 100/10=10 | 1g 100 -1g 10=2-1=1 |
| (3)10→1 | 10-1=9 | 10/1=10 | 1g 10 -1g 1=1-0=1 |
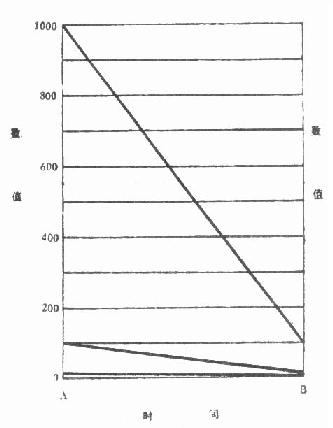
图 2 -7 三组数据绘在算术格纸上
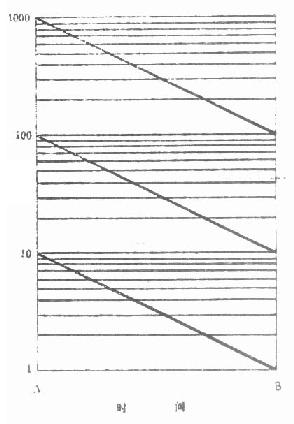
图 2 -8 三组数据绘在半对数格纸上
在算术格纸上三条直线的坡度相差悬殊,这是由 于三组数据的绝对差相差悬殊。在半对数格纸上三条直线平行,这是由于三组数据的对数差相等,图上反映出三组数据下降的幅度相同。
例如从表 2 -13 可看到细菌性痢疾的发病率最大值(45.37‰)为最小值(14.62‰)的 3 倍多,肺结核的最大值(3.65‰)为最小值 (0.52‰) 的 7 倍多。所以前者下降速度较慢,而后者较快,如果画在普通方格纸上,如图 02-9,将给人以错觉,而画在半对数纸上如图 2 -10,就能正确地表达两种疾病发病率下降速度的快慢。
绘制半对数线图时,横轴为算术尺度(是等距的),用来表示时间;而纵轴为对数尺度(是不等距的),用来表示被比较事物的某种率,纵轴尺度的标法,自 1 -10 为一组,上一组各数为下一组相应数的 10 倍。
表 2 -13 某部二十年来细菌性痢疾与肺结核的发病率 1958-1977
| 年份 | 发病率(‰) | 年份 | 发病率(‰) | ||
| 细菌性痢疾 | 肺结核 | 细菌性痢疾 | 肺结核 | ||
| 1958 | 30.22 | 3.65 | 1968 | 18.06 | 1.10 |
| 1958 | 45.37 | 2.32 | 1969 | 14.06 | 1.24 |
| 1960 | 38.84 | 2.12 | 1970 | 16.06 | 1.30 |
| 1961 | 28.41 | 2.31 | 1971 | 17.89 | 1.06 |
| 1962 | 24.33 | 2.59 | 1972 | 16.71 | 0.94 |
| 1963 | 28.20 | 2.30 | 1973 | 15.29 | 0.76 |
| 1964 | 19.41 | 1.86 | 1974 | 19.11 | 0.66 |
| 1965 | 24.26 | 1.31 | 1975 | 21.69 | 0.57 |
| 1966 | 25.24 | 1.27 | 1976 | 17.56 | 0.53 |
| 1967 | 22.30 | 1.26 | 1977 | 19.96 | 0.52 |
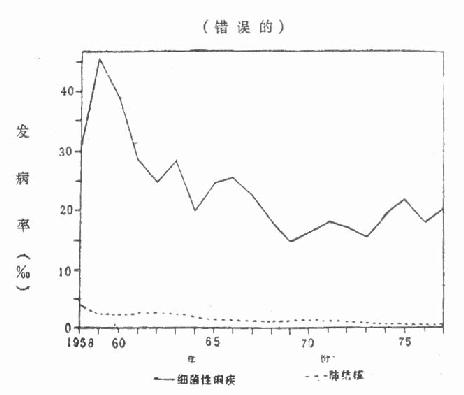
图 2 -9 某部二十年来细菌性痢疾与肺结核的发病率 1958-1977
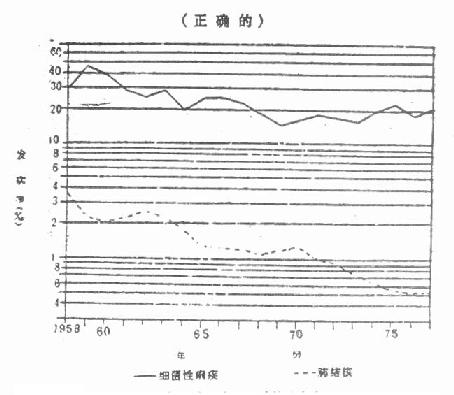
图 2 -10 某二十年来细菌性痢疾与肺结核的发病率 1958-1977
(五)直方图 直方图用矩形面积表示频数. 如图 2 -11 为我军某校部份同年龄同性别学员的身高分布, 资料见表 2 -14.
表 2 -14 我军××学校部分学员的身长分配
| 身长(厘米) | 152- | 156- | 160- | 164- | 168- | 172- | 176- | 180- | 184- | 188- | 合计 |
| 人数 | 1 | 10 | 28 | 56 | 52 | 34 | 12 | 5 | - | 1 | 199 |
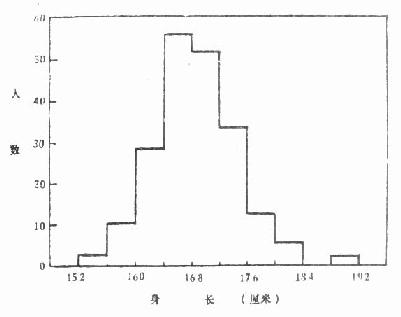
图 2 -11 我军××学校 199 学员的身长分配
当频数表的组距不等时,不能直接用各组频数绘制直方图,应先将组距化为相等,得出组距相等的各组的频数,再绘图,如表 2 -15 的组距不等,若用各组的患者人数绘制直方图,得图 2 -12,给人以错觉,好象 10~20 岁组的患者人数最多,其实这是组距不等造成的,因为 10 岁以前各组的组距为 1,而 10 岁以后各组的组距为 10 岁。因此,图 2 -12 不能正确反映真实情况,应先将组距化为 1,得出每岁平均患者人数,以此为矩形的高作图,如图 2 -13,才能正确表达出资料的实际情况。
绘制直方图的注意事项:
(1)直方图的的纵轴应从“0”开始,而横纵可以不从“0”点开始。
(2)直方图中各矩形之间可划直线隔开,也可以不划。
(3)当各组的组距不等时,不能直接用各组频数绘图,需要象表 2 -15 那样处理(通常是将频数除以组距作高度)后再作图,否则会给人以错误印象或概念。
表 2 -15 ×年×市流行性乙型脑炎患者的年龄分布
| 年岁 | 0- | 1- | 2- | 3- | 4- | 5- | 6- | 7- | 8- | 9- | 10- | 20- | 30- | 40- | 50- | 合计 |
| 人数 | 3 | 3 | 9 | 11 | 23 | 22 | 11 | 14 | 8 | 6 | 36 | 13 | 11 | 4 | 1 | 175 |
| 每岁患者人数 | 3 | 3 | 9 | 11 | 23 | 22 | 11 | 14 | 8 | 6 | 3.6 | 1.3 | 1.1 | 0.4 | 0.1 | - |
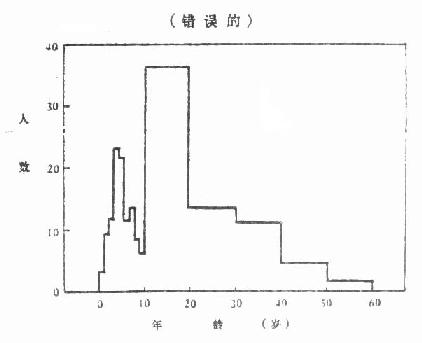
图 2 -12 ×年×市流行性乙型脑炎患者的年龄分布
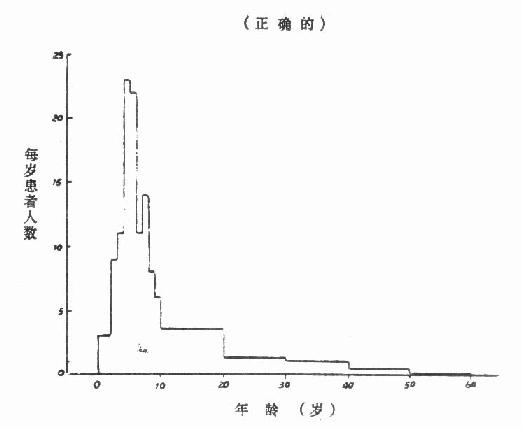
图 2 -13 ×年×市流行性乙型脑炎患者的年龄分布
7. 统计地图
统计地图用以表示事物 (或现象) 在地域上的分布情况, 多用点、线、颜色、符号等在地图上表示某种现象的数量,图图 2 -14 为我军某部队一次痢疾流行时的患者分布情况。
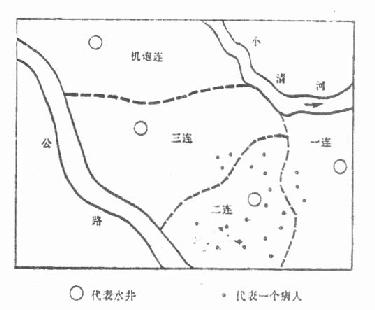
图 2 -14 某部队一次痢疾流行时的患者分布
练习题
1.统计图有哪几部分构成?制表的注意事项有哪些?
2.统计图有哪几部分构成?绘制统计图的注意事项有哪些?
3.如何根据资料的性质来选择适当的统计图形?
4.
(1)某中医研究院对 77 例治疗有效的慢性气管炎患者,停药两周后作了随访,结果如下表。试修改些表。
| 疗效分类(随访前) | 临床基本控制 | 显效 | 好转 | |||||||||
| 例 数 | 20 | 36 | 21 | |||||||||
| 停药两周后疗效随访结果 | 基本控制 | 显效 | 好转 | 无效 | 基本控制 | 显效 | 好转 | 无效 | 基本控制 | 显效 | 好转 | 无效 |
| 例 数 | 15 | 2 | 2 | 1 | 8 | 15 | 7 | 6 | 6 | 5 | 7 | 3 |
(2)某医院用中药细辛治疗“阿弗他性口炎”106 例初步观察
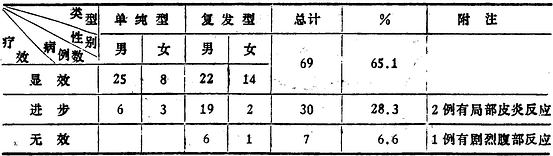
5.根据下列统计资料试作统计图。
(1)某地居民粪便中蠕虫卵两次检查结果
| 第一次阳性率(%) | 第二次阳性率(%) | |
| 钩 虫 | 61.22 | 31.36 |
| 蛔 虫 | 91.43 | 86.39 |
| 鞭 虫 | 17.14 | 16.51 |
(2) 痢疾杆菌药敏试验结果
| 制菌药物 | 试验株数 | 敏感度百分比(%) | ||||
| 高敏 | 中敏 | 轻敏 | 不敏 | 合计 | ||
| 老鹳草煎剂 | 243 | 48.5 | 30.4 | 16.1 | 5.0 | 100 |
| 丹贞合剂 | 250 | 53.2 | 36.4 | 10.4 | - | 100 |
| 呋喃唑酮 | 250 | 20.8 | 49.2 | 26.8 | 3.2 | 100 |
(3) 某部队 1977 年各月传染病发病人次
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 合计 |
| 传染病发病人次 | 3 | 4 | 7 | 14 | 9 | 14 | 17 | 104 | 58 | 12 | 5 | 2 | 249 |
(4) 224 例胸膜炎病人的年龄分配
| 病人年龄 | 各组人数占全部病人的百分比 |
| 11- | 4.1 |
| 16- | 13.5 |
| 21- | 44.6 |
| 31- | 27.1 |
| 41- | 8.9 |
| 51- | 1.8 |
| 合 计 | 100.0 |
(5) 某地 1951-1956 年肺结核、白喉的死亡专率
| 病 名 | 历年死亡专率(每十万人) | |||||
| 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | |
| 肺结核 | 164.4 | 135.8 | 79.9 | 64.7 | 74.5 | 63.0 |
| 白喉 | 18.7 | 2.5 | 2.5 | 1.0 | 1.2 | 1.0 |
第一节 X2 检验
X2(称卡方)检验用途较广,但主要用于检验两个或两个以上样本率或构成比之间差别的显着性,也可检验两类事物之间是否存在一定的关系。
一、两个率的比较
(一)X2检验的基本公式 下页末行的例 3.1 是两组心肌梗塞病人病死率的比较,见表 3.5,其中对照组未用抗凝药。两组病人的病死率不同,抗凝药组为 25.33%,对照组为 40.8%。造成这种不同的原因可能有两种:一种是仅由抽样误差所致;另一种是两个总体病死率确实有所不同。为了区别这两种情况,应当进行 X 2检验。其基本步骤如下:
1.首先将资料写成四格表形式,如表 3.6。
将每个组的治疗人数分为死亡与生存两部分,各占四格表中的一格,这些数字称为实际频数,符号为 A,即实际观察得来的数字。
2. 建立检验假设 为了进行检验,首先作检验假设:两种疗法的两总体病死率相等,为 35%(即 70/200),记为 H:π1=π2。即不论用或不用抗凝药,病死率都是 35%,所以亦可以换一种说法:病死率与疗法无关。
上述假设经过下面步骤的检验后,可以被接受也可以被拒绝。当 H 被拒绝时,就意味着接受其对立假设即备择假设 H 1。此例备择假设为两总体病死率不相等,记为 H 1:π1≠π2
因为我们观察的是随机现象,所以无论是接受或拒绝 H 都冒有一定风险,即存在着错判的可能性。一般要求,当错误地被拒绝的概率 α 不超过一定的数值,如 5%(或 0.05),此值称为检验水准,记为 α =0.05。
3.计算理论频数 根据“检验假设”推算出来的频数称理论频数,符号为 T。计算方法如下:假设两总体病死率相同,都是 35.0%,那么抗凝血组治疗 75 人,其死亡的理论频数应为 75×35.0%=26.25 人,而生存的理论频数为 75-26.25=48.75 人。用同样方法可求出对照组的死亡与生存的理论频数,前者为 43.75 人。后者为 81.25 人。然后,把这些理论频数填入相应的实际频数格内,见表 3.6 括号内数字。
计算理论频数也可用下式(3.4)
TRC=nRnC/N(3.4)
式中,TRC为 R 行与 C 列相交格子的理论频数,nR为与计算的理论频数同行的合计数,nC为与该理论频数同列的合计数,N 为总例数。
例如;表 3.6 第一行与第一列相交格子的理论频数(T11)为
T11=75×70/200=26.25
用两种方法计算,结果是相同的。
4.计算 χ 2值,计算 χ 2值的基本公式为:
X2=∑(A-T)2/t(3.5)
式中,A 为实际频数,T 为理论频数,∑为求和符号。
将表 3.6 里的实际频数与理论频数代入式(3.5)即求得 χ 2值。此例 χ 2=4.929。
从式 3.5 中可看出,实际频数与理论频数之差(A-T)愈小,所得的 χ 2值就愈小,理论频数是根据检验假设推算出来的,若与实际频数相差不大,说明假设与实际情况符合,于是就接受 H,认为两病死率无显著差别;反之,若(A-T)大,则 χ 2值亦大,说明假设与实际不符,就拒绝假设,认为两病死率有差别。但 χ 2值大还是小,要有一个比较的标准,要查 χ 2值表(附表 1),查 χ 2值表前先要定自由度。
5.求自由度 自由度是数学上的一个名词。在统计中,几个数据不受任何条件(如统计量,即样本特征数)的限制,几个数据就可以任意指定,称为有几个自由度。若受到 P 个条件限制,就只有 n - p 个自由度了。例如在四格表中有四个实际频数,如没有任何条件限制,则 4 个数字都可任意取值,有 4 个自由度,当 a +b,,c+d,a+c,b+ d 都固定后,在 a、b、c、d 四个实际频数中,只能有一个频数可任意指定了,因此,四格表的自由度为 1。其计算公式为:
ν=(R-1)(C-1)(3.6)
式中,ν 为自由度,R 为横行数,C 为纵列数。
四格表有 2 行和 2 列(注意:总计与合计栏不算在内)。因此 ν =(2-1)(2-1)=1。
6.求 P 值,作结论 根据自由度查 χ 2值表(附表 1)。此表的左侧 ν 为自由度,表内数字 χ 2值,表的上端 P 是从同一总体中抽得此样本 χ 2值的概率。三者关系是:在同一自由度下,χ2值越大,从同一总体中抽得此样本的概率 P 值越小;在同一 P 值下,自由度越大,χ2值也越大。χ2值与概率 P 呈相反的关系。χ2检验的常用界值为:
χ2<χ20.05()P>0.05 在 α =0.05 水准处接受 H,差别不显著
χ20.05≤χ2<χ20.01()0.05≥P>0.01 在 α =0.05 水准处拒绝 H O,接受 H 1,差别显著
χ2≥χ20.01()P≤0.01 在 α =0.01 水准处拒绝 H O,接受 H 1,差别显著
这里 α 是预定的检验水准。χ20.05()是当自由度为 ν 时与 P =0.05 相对应的 χ 2值,简称 5% 点,χ20.01()是与 P =0.01 相对应的 χ 2值,简称 1% 点。
当 ν = 1 时,χ20.05(1)3.84,χ20.01(1)=6.63。本例自由度为 1,求得 χ 2=4.929, 介于 3.84 与 6.63 之间,或写成 χ 20.05(1)<χ2<χ20.01(1)。由于与 3.84 对应的纵行 P =0.05,与 6.63 对应的纵行 P =0.01,因此与样本 χ 2=4.929 相应的概率介于 0.05 与 0.01 之间,写成 0.05>P>0.01。在 α =0.05 水准处拒绝 H,接受 H 1,两总体率不等。对照组的病死率较抗凝血组高。
在 α =0.05 水准处拒绝 H,说明若在同样情况下作 100 次判断,将有 5 次或不到 5 次的机会,将原没有差别的两总体率错判为有差别,或说这样判断犯 I 型错误的概率不超过 5%。
下面将实例的检验步骤集中列出。
例 3.1 两组心肌梗塞病人的病死率可见于表 3.5,其中对照组未用抗凝药。抗凝血组病死率为 25.33%,对照组为 40.80%,问两组病死率有无显著差别?
表 3.5 两组心肌梗塞病人病死率比较
| 组别 | 治疗人数 | 死亡人数 | 病死率(%) |
| 抗凝血组 | 75 | 19 | 25.33 |
| 对 照 组 | 125 | 51 | 40.80 |
| 总 计 | 200 | 70 | 35.00 |
检验步骤如下:
1.将资料列成四格表形式,如表 3.6。
表 3.6 四格表式样
| 死亡 | 生存 | 合计 | |
| 抗凝血组 | 19(26.25) | 56(48.75) | 75 |
| 对照组 | 51(43.75) | 74(81.25) | 125 |
| 总 计 | 70 | 130 | 200 |
2.H:两疗法的总体病死率相同,即π1=π2
H1:两疗法的总体病死率不同,即π1≠π2
α=0.05
3.求理论频数
抗凝血组:
死亡人数为 75×35.0%=26.25 人
存活人数为 75-26.25=48.75 人
对照组:
死亡人数为 125×35.0%=43.75 人
存活人数为 125-43.75=81.25 人
把理论频数填入相对应的实际频数格内,见表 3.6 括号内数字。
4.求 χ 2值 将表 3.6 里的数值代入式(3.5)得,
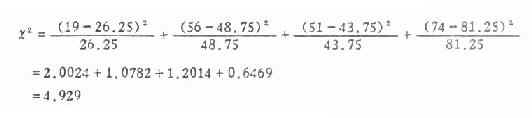
5.求自由度,确定 P 值,作结论
ν=(2-1)(2-1)=1,χ20.05(1)=3.84,χ20.01(1)=6.63,
本例 χ 2=4.929,χ20.05(1)<χ2<χ20.01(1),则 0.05>P>0.01,在 α =0.05 水准处拒绝 H,接受 H 1,即两总体病死率不等,对照组病死率较抗凝血组高。
上例告诉我们,两个样本病死率一大一小,在未作检验之前,很难说它们两总体率是否有差别,为了作出正确判断,作 X 2检验。先假设两总体病死率相同,推算理论频数,由实际频数与理论频数计算 χ 2值,二者相差越大,χ2值也越大。本例得 χ 2=4.929,根据自由度为 1 时的 χ 2分布推断,从同一总体内抽样,出现 χ 2值等于或大于 4.929 的概率较小,每一百次中在 5 次以下,1 次以上,因此检验假设被拒绝,而判断为有显著差别。
(二)连续性校正公式 χ2 检验是以连续的光滑曲线做根据的,当自由度为 1 时,χ2检验所得的概率容易偏低,因些需要校正,校正后的 χ 2值比不校正的小一些,校正公式是:
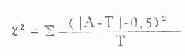 (3.7)
(3.7)
公式中 A - T 前后两条直线是绝对值的符号。
将表 3.5 资料代入式(3.7)得:
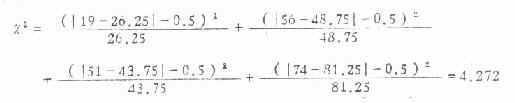
检验两个率相差的显著性时(此时自由度为 1),理论上都可用校正公式。但当用公式(3.5)求出的 χ 2值小于 3.84 时,相应的 P 值大于 0.05,表示两个率相差不显著,校正后 χ 2值更小,仍得同样结构,就无须校正;当用未校正公式求出的 χ 2值远远超过 3.84 时,校正后的结论仍相同,在此种情况下也可不校正;当自由度为 2 及以上时,则不必校正。
当用公式(3.5)求出的 χ 2值略大于 3.84 时,校正最为必要,往往会改变原来的结论,举例如下。
例 3.2 表 3.7 是六六六粉的两种配方进行野外烟剂灭黄鼠实验的观察结果。
表 3.7 六六六粉两种配方灭黄鼠的效果
| 烟薰后鼠洞情况 | 合 计(实验观察洞数) | 灭洞率(%) | ||
| 未盗开 | 盗 开 | |||
| 04 号配方 | 13(16.63) | 9(5.37) | 22 | 59.1 |
| 05 号配方 | 80(76.37) | 21(24.63) | 101 | 79.2 |
| 总 计 | 93 | 30 | 123 | 75.6 |
现用公式(3.5)及式(3.6)分别计算 χ 2值如下:

校正后的 χ 2值小于 3.84,P>0.05,在 α =0.05 的水准处接受 H,认为两种配方灭黄鼠效果无显著差异,这相结论是比较合理的,如果不经校正就会得出错误的结论。
(三)四格表中求 χ 2的专用公式 用上述基本公式(3.5)求 χ 2值,需要求出与实际频数一一对应的理论频数,运算较繁。在四格表中,用下列专用公式较为简便。
 (3.8)
(3.8)
式中 a、b、c、d 为四格表中的实际频数,N 表示总例数(即 N =a+b+c+d)。
现仍以表 3.5 资料为例,先写成四格表形式,如表 3.8。
表 3.8 四格表求 χ 2值专用公式的符号
| 死 亡 | 生存 | 合 计 | |
| 抗凝血组 | 19(a) | 56(b) | 75(a+b) |
| 对照组 | 51(c) | 74(d) | 125(c+d) |
| 70(a+c) | 130(b+d) | 200(N) |
将实际频数代入式(3.8)得,
![]()
这里用专用公式求得的 χ 2值与前面用基本公式求得的结果完全不同,有时这两个公式求得的结果小数点后几位可能稍有出入,这是由于受小数四舍五入的影响。
前面已介绍了连续性校正公式(3.7),为使运算更为简便,下面列出专用公式的连续性校正公式(3.9),并以表 3.8 资料代入计算如下:
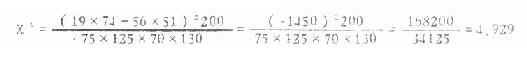 (3.9)
(3.9)
所得结果与式 (3.7) 求得的一致。
二、多个率或多个构成比的比较
(一)2×K 表的专用公式 ,前面已讨论了,两个率的比较用四格表专用公式计算 χ 2 值较为简便。如果是多个率比较,就要列成 2×K 表。这里的 K 暂为所比较的组数,2 为每个组内所划分的类型数。求 χ 2值时本可用基本公式计算,但以用下列专用公式为便:
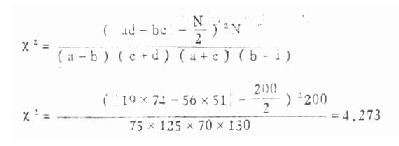 (3.10)(3.11)
(3.10)(3.11)
表 3.9 2×K 表形式之一
| a1 a2 ┆ ┆ | b1 b2 ┆ ┆ | n1 n2 ┆ ┆ |
| ∑ai | ∑bi | N |
公式中符号的意义参阅表 3.9,以上两个公式的计算结果是完全一样的。
例 3.3 某地观察磺胺三甲氧吡嗪加增效剂(吡嗪磺合剂)预防疟疾复发的效果,用已知有抗疟疾复发效果的乙胺嘧啶和不投药组作对照,比较三组的疟疾复发率,资料如表 3.10,问三组复发率有无显著差别?
表 3.10 三个组的疟疾复发率
| 组 别 | 观察例数 | 复发例数 | 复发率(%) |
| 吡嗪磺合剂 乙胺嘧啶 对 照 | 1996 473 484 | 76 27 53 | 3.81 5.71 10.95 |
| 合 计 | 2953 | 156 | 5.28 |
χ2检验步骤如下:
1.将表 3.10 资料写成 2×K 表形式,见表 3.11。注意:这里必须把各组的观察例数分为复发和未复发两部分,这样表 3.10 就为写成 2×3 表。
表 3.11 三个组疟疾复发率的比较
| 复发 | 未复发 | 合 计 | |
| 吡嗪磺合剂 | 76 | 1920 | 1996 |
| 乙胺嘧啶 | 27 | 446 | 473 |
| 对 照 | 53 | 431 | 484 |
| 合 计 | 156 | 2797 | 2953 |
2.H:三个总体复发率相同
H1:三个总体复发率不全相同
α=0.05
3.求 χ 2值 将表 3.11 的数值代入式(3.10)(因为在表 3.11 中,各组的 a 值较小,计算较方便)得:
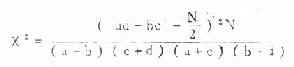
4.求自由度,确定 P 值,作结论
ν=(K-1)(2-1)=(3-1)(2-1)=2,查 χ 2值表得 χ 20.01(2)=9.21,本例 χ 2=39.92>χ20.01(2),P<0.01, 在 α =0.05 的水准处拒绝 H,接受 H 1,即三个组的复发率有显著差别。
本例的结论是三个组的复发率有显著差别,因此,还需进一步说明三组中那两组有差别,可用四格表对每两个率进行假设检验。本例的检验结果是:吡嗪磺合剂与对照组比(P<0.01),乙胺嘧啶组与对照组比(P<0.01),而吡嗪磺合剂与乙胺嘧啶比(P>0.05),说明吡嗪磺合剂有预防疟疾复发的作用,其效果不低于乙胺嘧啶。
本例 2×K 表的 2 是指得发、未复发两项,K 为比较的组数,K=3。如果比较组数只有 2,而构成每组的项数则多于 2,如甲状腺肿的型别构成可分为弥漫型、结节型、混合型三种。这类资料亦同样可用 2×K 表专用公式进行检验。这时把 2 作为比较组数,K 作为项数,检验方法同上,表 3.12 是 2×K 表的另一种形式。
表 3.12 2×K 表形式之二
| a1 | a2 | …… | ∑ai∑bi |
| b1 | b2 | …… | |
| n1 | n2 | …… | N |
例 3.4,为研究不同地域甲状腺型别的构成有无显著差别,某省对两个县的居民进行甲状腺肿调查,得资料如表 3.13,问甲乙两县各型甲状腺肿患者构成比有无显著判别?
表 3.13 某省甲乙两县甲状腺肿患者型别构成比较
| 县名 | 弥漫型 | 结节型 | 混合型 | 合计 |
| 甲县 | 486 | 2 | 4 | 492 |
| 乙县 | 133 | 260 | 51 | 444 |
| 合计 | 619 | 262 | 55 | 936 |
检验步骤如下:
1.H:两总体甲状腺肿型别构成相同
H1:两总体甲状腺肿型别构成不同
α=0.05
2.求 χ 2值,将表 3.13 中的数值代入式 3.10 得:
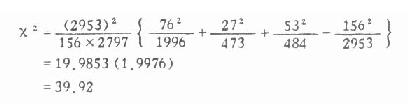
3.求自由度,确定 P 值,作结论。
ν=(3-1)(2-1)=2,查 χ 2值表得 χ 20.01(2)=9.21, 本例,χ2=494.36,P<0.01, 在 α =0.05 水准处拒绝 H,接受 H 1,甲、乙两县甲状腺肿型别构成有差别(P<0.01)。甲县以弥漫型为主,而乙县结节型较多,地域与患者的型别构成具有一定的关系。
此类资料经 χ 2检验作结论,如果不显著,说明两组资料的构成比来自同一总体,没有显著差别。如果结论显著,说明两组的构成比来自不同总体,差别有显著性。同时要指出两组构成的主要区别。
(二)R×C 表的通用公式 当资料的行数和列数都超过 2 时称 R×C 表。对此种资料作假设检验时,可用基本公式(3.5), 但运算较繁,如果用 R×C 表的通用公式计算 χ 2值,较为简便。
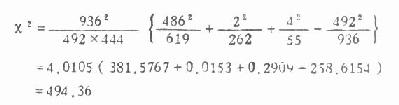 (3.12)
(3.12)
式中,Aij为 i 行第 j 列的实际频数,ni为第 i 行的合计数,nj为第 j 行列的合计数,N 为总频数。
这个公式也系由基本公式(3.5)推导出来,式(3.12)也可用以求四格表、2×K 表资料的 X 2值,故称通用公式,用此公式不需计算理论频数,与基本公式(3.5)相比,较为简便。
例 3.5 某院肝胆外科在手术中观察了胆结石的部位与类型得资料如表 3.14, 试分析两者间有无关系存在?
表 3.14 胆结石类型与部位的关系
| 结石部位 | 总例数 | 例 数 | 百 分 比 | ||||
| 胆固醇结石 | 胆红素结石 | 其它 | 胆固醇结石 | 胆红素结石 | 其它 | ||
| 胆囊 | 118 | 70 | 16 | 32 | 59.3 | 13.6 | 27.1 |
| 肝外胆管 | 75 | 12 | 39 | 24 | 16.0 | 52.0 | 32.0 |
| 肝内胆管 | 29 | 2 | 20 | 7 | 6.9 | 69.0 | 24.1 |
| 合计 | 222 | 84 | 75 | 63 | 37.8 | 33.8 | 28.4 |
检验步骤如下:
1.将表 3.14 资料写成 R×C 表形式,见表 3.15.
表 3.15 胆结石类型与部位的关系
| 结石部位 | 结 构 类 型 | ||||
| 胆固醇结石 | 胆红素结石 | 其它 | 合计 | ||
| 胆囊 | 70 | 16 | 32 | 118 | |
| 肝外胆管 | 12 | 39 | 24 | 75 | |
| 肝内胆管 | 2 | 20 | 7 | 29 | |
| 合计 | 84 | 75 | 63 | 222 | |
2.H:胆结石的类型与部位没有关系
H1:胆结石的类型与部位有关系
α=0.01
3.求 χ 2值 将表 3.15 数值代入式(3.12)得:
![]()
4.求自由度,确定 P 值,作结论。
ν=(3-1)(3-1)=4,查 χ 2值表得 χ 20.01(4)=13.28,本例 χ 2=64.06<χ20.01。在 α =0.01 水准处拒绝 H,接受 H 1,胆结石类型与部位有显著关系存在(P<0.01), 胆囊内以胆固醇结石居多,肝内、外胆管以胆红素结石为主。
第二节 X2 检验的注意事项
(一)计算 χ2 值时,必须用绝对数,而不能用相对数,因为 χ2 值的大小与频数大小有关。
(二)当自由度为 1 时,需考虑进行连续性校正,当求出的 χ2 值略大于 3.84 时,校正更为必要。因为往往会改变原来的结论。
(三)多组资料进行 χ2 检验时,如理论频数小于 5 的个数占全部理论频数个数的五分之一以上时,要进行适当的并组,但应注意,要并得合理,若比较几个等级资料相差是否显着时,用 Ridit 分析法或秩和检验为好。
(四)假设检验的结论,只提示两样本从同一总体中抽得的概率。当两种疗法的病死率相差显著时,并不证明某疗法疗效差,只是说两样本从同一总体抽得的概率小,因此可能两样本来自不同的总体,差别有意义。当相差不显著时,并不证明两疗法疗效相同,只是说两样本来自同一总体的可能性大,因此,作出有判别的结论,数据不足,至于有、无差别的理由,要从专业上加以探讨:差别的大小,要根据医学上的实际意义来评论。
(五)进行假设检验的资料应合乎随机抽样原则,且各组除处理因素不同外,其他条件应尽量控制其相同。下结论时,不能绝对化,因为显著性界限是人为规定的,相对的。即使是根据 P <0.01 作出的结论,仍有 1% 错误的可能。当检验结果与显著性界限很接近时,可加大样本继续观察,不要急于下结论。
第三章 平均数与变异指标
上章介绍了计数资料的整理与分析,从本章开始介绍计量资料的整理与分析。通过调查或实验收集到的计量资料,是一群大大小小的变量值。为将这群变量值的特点描述出来,当例数较多时,可先编制成频数表,了解变量值的分布情况,然后计算平均数描述其集中位置,计算变异指标描述其离散程度;若倒数较少,亦可直接计算平均数与变异指标。现分述于下。
第一节 平均数
一、频数表的编制与频数分布
计量资料有离散型变量和连续型变量。对离散型变量,可列出变量值及其频数如表 4.1。若变量值较多时,亦可用组段表示如表 4.2。每个组段的起点称下限,终点称上限,上限与下限之差称组距。如表 4.2 第一组的下限是 0,上限是 1。第二组的下限是 2 上限是 3,组距都是 1。归组以后,该组的变量值用组段的中值代表,称组中值。如第一组的组中值为 0.5。
表 4.1 某市居民 1095 天中每天意外死亡人数(1980~82 年)
| 死亡人数 | 天数 |
| 807 | |
| 1 | 250 |
| 2 | 31 |
| 3 | 5 |
| 4 | |
| 5 | |
| 6 | |
| 7 | 1 |
| 8 | |
| ┆ | ┆ |
| 15 | 1 |
| 合 计 | 1095 |
表 4.2 204 名轧钢工人白细胞中大单核所占百分比
| 大单核数(个 / 每百白细胞) | 人数 |
| 0-1 | 24 |
| 2-3 | 40 |
| 4-5 | 55 |
| 6-7 | 37 |
| 8-9 | 27 |
| 10-11 | 18 |
| 12-13 | 1 |
| 14-15 | |
| 16-17 | 1 |
| 18-19 | |
| 20-21 | 1 |
| 合计 | 204 |
若是连续型变量,组段的写法与离散型变量的略有不同。如表 4.3 坐高第一组段下限为 61,上限为 62;第二组段的下限为 62,上限为 63。因此,上一组段的上限和下一组段的下限值相同。为便于归组,上限一般不写出来。如第一组写成“61-”,意思是凡坐高在 61 至未离散型变最的数值较大时,亦可按连续型变量写组段,如红细胞数(万 /mm3)的组段应写成 400-419,420-439,…,亦可简化写成 400-,420-,…。这样由组段和频数两部分组成的表称为频数表。下面用表 4.4 资料说明频数表编制步骤。
表 4.3 某市 7 岁男童坐高频数表

表 4.4 西安市 7 岁男童 102 人的坐高,cm
| 64.4 | 63.8 | 64.5 | 66.8 | 66.5 | 66.3 | 68.3 | 67.2 | 68.0 | 67.9 |
| 63.2 | 64.6 | 64.8 | 66.2 | 68.0 | 66.7 | 67.4 | 68.6 | 66.8 | 66.9 |
| 63.2 | 61.1 | 65.0 | 65.0 | 66.4 | 69.1 | 66.8 | 66.4 | 67.5 | 68.1 |
| 69.7 | 62.5 | 64.3 | 66.3 | 66.6 | 67.8 | 65.9 | 67.9 | 65.9 | 69.8 |
| 71.1 | 70.1 | 64.9 | 66.1 | 67.3 | 66.8 | 65.0 | 65.7 | 68.4 | 67.6 |
| 69.5 | 67.5 | 62.4 | 62.6 | 66.5 | 67.2 | 64.5 | 65.7 | 67.0 | 65.1 |
| 70.0 | 69.6 | 64.7 | 65.8 | 64.2 | 67.3 | 65.0 | 65.0 | 67.2 | 70.2 |
| 68.0 | 68.2 | 63.2 | 64.6 | 64.2 | 64.5 | 65.9 | 66.6 | 69.2 | 71.2 |
| 68.3 | 70.8 | 65.3 | 64.2 | 68.0 | 66.7 | 65.6 | 66.8 | 67.9 | 67.6 |
| 70.4 | 68.4 | 64.3 | 66.0 | 67.3 | 65.6 | 66.0 | 66.9 | 67.4 | 68.5 |
| 68.3 | 69.7 |
(一)找出原始资料中的最小、最大值 表 4.4 坐高的最大值为 71.2cm,最小值为 61.1cm,最大值与最小值之差称极差为 10.1cm。
(二)定组距 先考虑组数。资料在 100 例以上的一般分 10-15 组。若例数较少,组数可相应少些;例数很多,组数可酌情多些,以能显示分布的规律为宜。此例拟分 10 组。将拟分的组数除极差(10.1/10≈1)得组距的约数。再调整到较方便的数如 0.1、0.2、0.5,1、2、5、10、20、50……等。此例取组距为 1。
(三)写组段 取等于或略小于最小值的整数为第一组的下限。按组距依次写出各组段的下限及短横,见表 4.3 组段行,注意短横“-”不能略去。
(四)划线记数 像选举开票那样,将变量值逐个归入相应的组段,如将 64.4 归入“64-”组,63.8 归入“63-”组。每归入一个变量值,在相应的组段内划一竖线,每逢第五线则作一横线跨在已划出的四条竖线上,这样五线连在一起最后计数时就很方便了。划完后将每个组段内的线条数写出,再将各组频数合计,频数表就编好了。
若事先不能确定合适的组数,可先分细些,需要时再将相邻两组合并。而分粗了,再要分细,则只得重划。
表 4.4 的资料编成频数表(见表 4.3)后,可看出变量值的分布情况,若绘成直方图就更直观。从图 4.1 可看到横坐标约为 66.5cm 处直方最高,表示变量值围绕在 66.5 左右的最多;两侧对称下降,大于 66.5 和小于 66.5 的变量值个数基本相等。这种类型的分布为对称分布。第五章介绍的正态分布是其中最常见的一种。
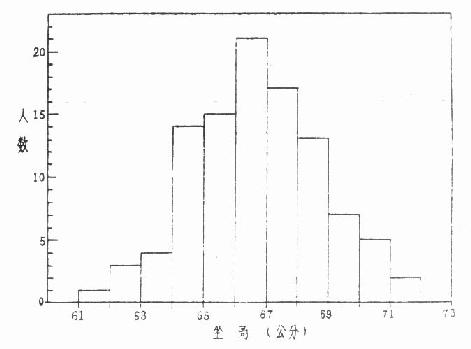
图 4.1 西安市 7 岁男童坐高分布
此外,如图 4.2,变量值愈小频数愈多图形呈“L”形,图 4.3 的频数集中在变量值较小的一边,右侧尾部拖得很长。后两种属偏态分布。这三种频数分布都只有一个高峰称单峰分布。为更准确地说明分布的特征,对形状相同的分布作出集中位置和离散程度的比较,就需计算频数分布的一些特别值。如平均数、百分位数、极差、标准差、变异系数等。
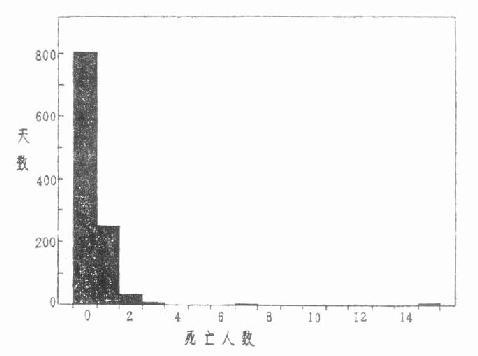
图 4.2 某市 1095 天中居民意外死亡人数(1980-1982)
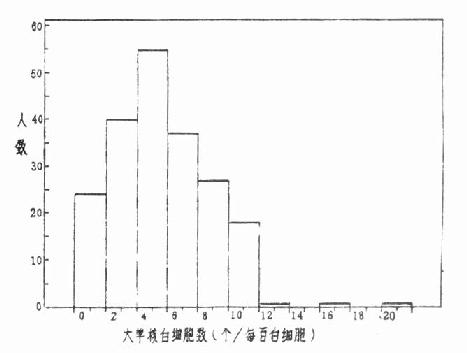
图 4.3 204 名轧钢工人白细胞中大单核所占百分比
二、众数、中位数、百分位数的意义及计算法
(一)众数 出现次数最多的变量值,或频数表上频数最多组的组中值即为众数。如表 4.3 中坐高的众数是 66.5cm。这样仅由观察所得的众数称为观察众数。同一资料常因所用组距不同和下限取值不同,观察众数稍有出入,故又称概约众数,与观察众数相对应的尚有理论众数。理论众数的算法根据频数曲线类型的不同而异,数学上为与极大值相应的横坐标。
(二)中位数及百分位数
1.中位数 将 n 个变量值从小到大排列后,居中的一数就是中位数,符号为 M,有的书上用 Md。它将变量值分为两半,一半比它小,一半比它大。
X1<x2<…<m<…xn-1<xa</x</m<…x</x
当 n 为奇数时
![]() (4.1)
(4.1)
当 n 为偶数时
 (4.2)
(4.2)
当资料呈明显偏态,或有个别的特小、特大值存在时,中位数的代表性往往比均数好。例如有 5 个变量值 8、9、9、10、19。其中 4 个在 9 左右,但由于受数值 19 的影响,均数为 11,不能很好代表中等水平。求中位数

比较符合实际。
根据频数表计算连续型变量的中位数可用式(4.3)或式(4.4)
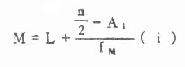 (4.3)
(4.3)
或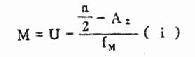 (4.4)
(4.4)
式中 L、U 分别为中位数所在组的下限及上限,A1为小于 L 的各组的累计频数,A2为大于 U 的各组的累计频数,fM、i 分别为中位数所在组的频数和组距。现用表 4.5 说明计算步骤如下:
(1)求出中位数的位置。在频数表上,数据已由小到大排好了。中位数将频数等分为 2,因此先计算 n /2,得中位数的位置。
n/2=157/2=78.5
(2)列出频数表、计算累计频数。列频数表时,组段的短横“-”写在两个组段下限之间,其意义仍与写在右边的相同,见表 4.5 第(1)栏。
第(3)栏为累计频数。此例自上而下累计到略小于 n / 2 为止得 A 1=41,表示住院天数为 10 天及以下的有 41 个人。若要知道第 78.5 人的变量值,就需要从 10-15 组内再累计(78.5-41=)37.5 人。假定该组的 49 人在 10-15 天内均匀分布着(见图 4.4),那么只要在 10 天上再加(78.5-41)/49 个组距便是中位数了。所以
![]()
用符号表示见式(4.3)。
若将频数自下而上累计到略小于 n / 2 为止,则得 A 2=67。也得出中位数在 10-15 组段内。
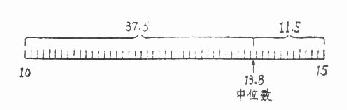
图 4.4 中位数计算示意图
(3)写出 L 或 U、fM及 i。
(4)代入公式得 M。
例 4.1 求杆菌痢疾治愈者 157 名住院天数的中位数。
n/2=157/2=78.5
表 4.5 杆菌痢疾治愈者的住院天数

L=10 或 U =15,fM=49,i=5。
代入公式
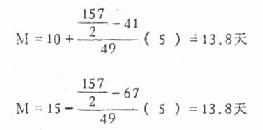
杆菌痢疾治愈者住院天数的中位数为 13.8 天。
中位数既然把频数等分为二,所以从另一端算起,用式(4.4)可得到同样的结果。
此例若计算治愈者平均住院天数得 17.9 天。从频数表上可看到 157 名患者中住院天数少于 15 天的就有 90 名,占 57.3%,因此中位数 13.8 天的代表性优于均数 17.9 天。
2.百分位数 中位数将频数等分为二,亦称二分位数。若将频数等分为四,则称四分位数,共有三个四分位数,即第一、第二、第三四分位数。第二四分位数即中位数。同理,将频数等分为十或一百的分位数称十分位数或百分位数。其实上述各种分位数都可用百分位数表示。百分位数的符号为 P x,X 代表第 X 百分位。例如第一四分位数、中位数可分别以 P 25、P50表示。计算百分位数的方法与中位数相似,只是式(4.3)中的 n / 2 以 nx/100 代替,M 以 X 代替。
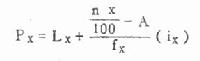 (4.5)
(4.5)
式中 L X、fx、ix分别为 P x所在组的下限、频数及组距。A 为小于 L x各组的累计频数。
例 4.2,求例 4.1 中住院天数的 P 90。
(1)计算![]()
(2)累计频数自上而下至略小于 141.3,见表 4.5 第(4)栏,得 A =135。知 P 90在 30-35 组内,因此 Lx=30,i=5,fx=7
(3)代入公式
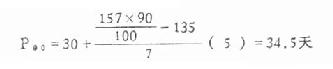
第 90 百分位数为 34.5 天,说明有 90% 的患者住院天数在 34.5 天以下。
三、算术均数与几何均数的意义及计算方法
(一)算术均数 简称均数。设观察了 n 个变量值 X 1,X2,……Xa,一般可直接用式(4.6)求样本均数 X。
![]()
式中∑是总和的符号,n 是样本含量即例数。本书在不会引起误解的情况下简写成
X=1/n∑X(4.6)
例 4.318-24 岁非心脏疾患死亡的男子心脏重量(g)如下,求心重的均数。
| 350 | 320 | 260 | 380 | 270 | 235 | 285 | 300 | 300 | 200 |
| 275 | 280 | 290 | 310 | 300 | 280 | 300 | 310 | 310 | 320 |
X=1/20(350+320+…+320)=5875/20=293.75g
样本均数是总体均数的估计值,它有两个特性。(1)∑(X-X)=0,(2)∑(X-X)2为最小,前者读者
可自证,后者证明如下:
设:a≠X,则 a=X±d d>0
∑(X-a)2=∑(X-X±d)2
=∑[(X-X)±d]2
=∑(X-X)2±2d∑(X-X)+Nd2
从第一个特性知∑(X-X)=0,因此 2d∑(X-X)=0,
得
∑(X-a)2=∑(X-X)2+Nd2
N 是例数,不可能为负,所以 Nd2也不会是负数。
∑(X-a)2>∑(X-X)2,∑(X-X)2为最小。
当用电子计算机处理大量实验数据,考虑到有较大舍入误差时,则先取一较近均数的常数 c,然后用式(4.7)计算,可提高均数的精度。
X=C+1/n×(Xi-C)(4.7)
若每输入一个变量值后都希望得到均数,那么可用式(4.8)
X=Xn-1+1/n×(Xn-Xn-1(4.8)
例 4.4 仍用例 4.3 资料,已算得前 19 例心重的 X 10=292.37, 又测得 X 20=320,求 X 20。
X20=292.37+1/20×(320-292.37)=293.75g
若相同的变量值个数较多,或对频数表资料求均数时,可用式(4.9)计算 X。
![]() 或简写为 X=1/n∑fX (4.9)
或简写为 X=1/n∑fX (4.9)
式中 K 为不同变量值个数,或频数表中的组段数。Xi 为第 i 个不同的变量值或频数表上的组中值,fi 为第 i 个变量值的频数。
例 4.5 计算表 4.5 菌痢治愈者的平均住院天数。
X=1/157(3×2.5+38×7.5……+1×77.5)=17.9 天
式(4.9)中某变量值的频数愈大,则该变量值对 X 的影响亦愈大。因此,频数又称权数,这样
计算出来的均数又叫加权均数。亦有根据变量值的重要性进行加权,计算加权均数的。
(二)几何均数 设 n 个变量值 X 1,X2,……,Xa 呈对数正态分布,其几何均数 G 为

式中∏为连乘的符号。当变量值较多时,乘积很大,计算不便,常改用下式计算
![]() (4.10)
(4.10)
或![]() (4.11)
(4.11)
式中符号含义同式(4.6)与式(4.9)。
例 4.6 求下表中麻疹病毒特异性 IgG 荧光抗体的平均滴度。
表 4.6 52 例麻疹患者恢复期血清麻疹病毒
特异性 IgG 荧光抗体滴度
| IgG 滴度倒数 | 例数 |
| 40 | 3 |
| 80 | 22 |
| 160 | 17 |
| 320 | 9 |
| 640 | |
| 1280 | 1 |
G=log-1[1/52×(3log40+22log80+…+log1280)]=129.3
麻疹患者恢复期血清麻疹病毒特异性 IgG 荧光抗体的平均滴度为 1:129。
式(4.10)包含三个步骤,(1)令 X i=logXi,则式(4.10)可写成![]() ;(2)1/n∑Xi
;(2)1/n∑Xi
即对数数值的均数 X;(3)将 X 取反对数即得几何均数 1og-1X=G。这里不难理解,若将这种资料作对数变换后,即可用式(4.6)至式 (4.9) 的各式计算均数,得到结果后再取反对数即得几何均数。读者可自已验证。
四、运用平均数的注意事项
平均数是描述一群同质变量值集中位置的特征值,用来说明某现象或事物数量的中等水平。通常用平均数作为算术均数、几何均数、众数、中位数等的统称,而以均数作为算术均数的简称。
1.同质的事物或现象才能求平均数 我们检查 200 名正常人的红细胞数(万 /mm3)计算平均数,定出正常值范围,作为诊断贫血的依据之一。如果正常人中混有贫血患者,那么求出的平均数既不能说明正常人也不能说明贫血患者,有人把它称为虚构的平均数,因为它模糊了数量特征,不能提供分析的依据了。因此计算平均数以前必须考虑资料的同质性。有人研究某药物的利尿作用,观察了二条狗、三头兔子用药前后的排尿滴数,曾将狗与兔子的排尿滴数加在一起求平均数。由于狗体大,排尿滴数较兔子的多,得到的平均数对狗来说似嫌少,而对兔子来说又显得太多,这是虚构平均数的又一例。
像狗与兔子,贫血患者与正常人的不同质是显而易见的。但即使是正常人,性别、年龄、地区不同,红细胞数的均数也有差异。那么怎样才算是同质呢?是否同质,要根据研究目的而定。例如研究痢疾患者的平均治愈日数时,要考虑不同病原菌、不同型别(急性、慢性等)的患者是不同质的。但当研究传染病的住院日数时,则不同疾病(痢疾、伤寒、……)是不同质的,而所有痢疾病人,不论由何种病原菌引起,或是何种型别都认为是同质的了。若研究各医院的平均住院天数时,医院类型(传染病院、儿童医院、综合医院、……)以及同类医院中,科室(内、外、传染……)设置及床位分配不同等就是不同质的了。不同质的事物就要分组求平均数,以便分析比较。因此科学的平均数是建立在分组的基础上的。
2.用组平均数补充总平均数 表 4.7 是某院 1983 年的治愈者平均住院天数。总均数为 18 天。但从表中可见,它所包含的 20 类(其他类除外)的疾病中,变态反应及中毒、小儿科疾病住院天数最短为 9 天,而结核病的却长达 60 天。住院天数高于总均数的有 10 类,治愈人数共 1358 人,占治愈总人数(其他类除外)的 35%。若医疗质量基本不变,多收结核病人,住院天数的总均数无疑会延长;而多收小儿患者,总均数就会缩短。因此如没有收容病种的分析,仅从总均数的延长或缩短来看医疗质量是不科学的。而对各时期同种疾病的住院天数进行分析,比较适宜。
表 4.7 某医院 1983 年各类疾病治愈者的平均住院天数
| 病类 | 治愈人数 | 平均住院天数 | 病类 | 治愈人数 | 平均住院天数 |
| 传染病寄生虫病 | 437 | 13 | 外科疾病 | 549 | 18 |
| 结核病 | 109 | 60 | 外伤 | 383 | 28 |
| 呼吸系疾病 | 246 | 14 | 肿瘤 | 65 | 34 |
| 消化系疾病 | 255 | 24 | 眼科疾病 | 112 | 14 |
| 内分泌疾病 | 41 | 35 | 耳鼻喉科疾病 | 417 | 10 |
| 循环系疾病 | 34 | 37 | 口腔科疾病 | 30 | 12 |
| 血液及造血系统疾病 | 7 | 33 | 皮肤科疾病 | 224 | 22 |
| 神经系疾病 | 111 | 25 | 妇产科疾病 | 78 | 12 |
| 变态反应及中毒 | 43 | 9 | 小儿疾病 | 601 | 9 |
| 风湿病 | 21 | 10 | 其他 | 35 | 19 |
| 泌尿系疾病 | 129 | 21 | 合计 | 3927 | 18 |
3.根据资料的分布选用适当的平均数 计量资料如是单峰对称分布,宜用均数,亦可用中位数。若是偏态分布则中位数的代表性常较均数为好。某些传染病的潜伏期、抗体滴度、细菌计数、率或比的变化速度及某些物质浓度等,其频数分布明显偏态,但经对数代换后近于正态分布的,如图 4.3 资料,应计算几何均数以描述其中等水平。
第二节 变异指标
一、变异指标的意义及种类
设有甲乙两人,对同一名患者采耳垂血,检查红细胞数(万 /mm3),每人数五个计数盘,得结果为
| 合计 | 均数 | ||||||
| 甲 | 480 | 490 | 500 | 510 | 520 | 2500 | 500 |
| 乙 | 440 | 460 | 500 | 540 | 560 | 2500 | 500 |
两人计数的均数都是 500,能说两人的检验技术相同吗?不能,因为甲的计数结果比较密集,而乙的分散,因此甲的检验精度显然比乙的高。从上可以看出:描述一群变量值,除用平均数等表示其集中位置外,还要说明其分散或变异情况。说明变异情况的特征值称变异指标。变异指标的种类较多,下面分别介绍极差、四分位数间距、均差、方差、标准差及变异系数。
1.极差 最大值与最小值之差称极差(或全距),符号为 R,是变异指标中最简单的一种。如上例甲计数的极差为 520-480=40,乙的为 560-440=120。可见乙的计数较甲的波动大。一般把最小值与最大值写在括号里,附在极差的后面。如上例写成 40(480~520)与 120(440~560)。其单位与变量值的相同。
当调查例数增多时,遇到较大或较小极端值的机会就加大,因此最大值与极差随着例数的增多而加大,但最小值却随着例数的增多而变小。
极差计算简便,但只考虑了最小、最大值,因此易受个别极端值的影响,且随例数的多少而变动,不稳定。仅用于粗略地说明变量值的变动范围。但在正态分布中可用以估计标准值范围,详见有关文献。
2.四分位数间距 极差的不稳定主要是受两极端数值的影响,于是有人将两端数据按比例去掉一定例数,这样所得数据就比较稳定了。例如两端各去掉 25%,取中间 50% 数据的数值范围,那么只要计算 P 25与 P 75,求 P 75与 P 25之差即得四分位数间距,符号为 Q。
Q=P75-P25(4.12)
例 4.7 试计算表 4.8 七岁男童坐高的四分位数间距
求 P25的位置 102×.25=.25.5.
求 P75的位置 102×.75=.76.5.
求累计频数得:
L25=65,L75=68,
A25=22,A75=75,
f25=15, f75=13,i=1
表 4.8 7 岁男童的坐高
| 坐高(cm) | 例数(f) | 累计频数 |
| 61- | 1 | 1 |
| 62- | 3 | 4 |
| 63- | 4 | 8 |
| 64- | 14 | 22 |
| 65- | 15 | 37 |
| 66- | 21 | 58 |
| 67- | 17 | 75 |
| 68- | 13 | 88 |
| 69- | 7 | 95 |
| 70- | 5 | 100 |
| 71- | 2 | 102 |
| 合计 | 102 | — |
代入式(4.5)得:
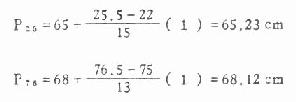
Q=68.12-65.23=2.89 cm
有 50% 的 7 岁男童,坐高在 65.23~68.12cm 之间,其四分位数间距为 2.89cm。
3.均差 四分位数间距虽比极差稳定,但仍只是两点之间的距离,没有利用每个变量值的信息。于是有人计算每个变量值与均数(或中位数)差的绝对值之和,然后平均称为均差(或平均直线差)作为变异指标之一。
![]() (4.13)
(4.13)
例 4.8 试计算 4.3 中,心重的均差。
由例 4.3 知 X =293.75g,代入式(4.13)得

4.方差 式式(4.13)中用变量值与均数之差的绝对值之和∑∣X-X∣,而不用离均差之和∑(X-X)是因为∑(X-X)=0,不能说明变异情况,故取绝对值以去掉负号。亦有人用平方的办法,即用离均差平方和∑(X-x)2,既去掉了负号,又提高了指标的灵敏性。因为数值愈大,平方后增大的愈多,所以离均差稍有变化,就能从指标上反映出来。例如有甲乙两组数据如下:
| X | ∑∣X-X∣ | ∑(X-X)2 | ||||||
| 甲组 | 10 | 11 | 12 | 13 | 14 | 12 | 6 | 10 |
| 乙组 | 9 | 12 | 12 | 13 | 14 | 12 | 6 | 14 |
乙组仅有两个数据与甲组的不同,这种不同从∑∣X-X∣或均差上是反映不出来的,但从∑(X-X)2上却反映出来了。以∑(X-X)2组成的变异指标有方差与标准差。方差是标准差的平方,将在第八章讨论,下面先介绍标准差。
二、标准差
1.标准差的公式 样本标准差是用得最多的变异指标,其公式为
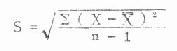 (4.14)
(4.14)
式(4.14)中的 n - 1 是自由度。n 个变量值本有 n 个自由度,但计算标准差时用了样本均数 X,因此就受到了一个条件即∑X= nX 的限制。例如有 4 个数据,它们的均数为 5。由于受到均数为 5 的限制,4 个数据中只有 3 个可以任意指定。如果任意指定的是 4、3、6,那么第 4 个数据只能是 7,否则均数就不是 5 了。所以标准差的自由度为 n -1。
2.标准差的计算
(1)按基本公式(4.14)计算
例 4.9 用例 4.3 资料计算心重的标准差。
已算得 X =293.75g,代入式(4.14)得
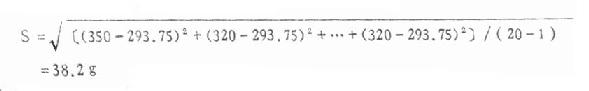
(2)递推法当用电子计算机进行计算,希望每输入一个数据,都能得到 X 与 S,则将式(4.8)与式
(4.5)配合计算。
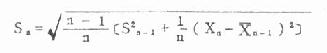 (4.15)
(4.15)
这里 S n表示 n 个数据的标准差,Sn-1表示 n - 1 个数据的标准差。Xn是第 n 个数据,Xn-1是 n - 1 个数据的均数。
例 4.10 仍用例 4.3 资料,已算得前 19 例心重的 X 19=292.37,S19=38.71。X20=320,代入式(4.15)得
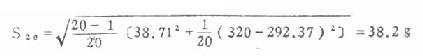
(3)直接法 不需先计算均数,直接用变量值代入式(4.16)或式 (1.17) 计算。
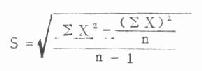 (4.16)
(4.16)
或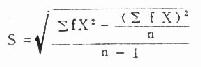 (4.17)
(4.17)
式(4.16)的分子是由式(4.14)的分子简化而得来的,证明如下。
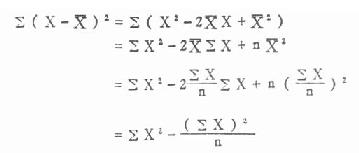
例 4.11 用 ELISA(酶联免疫吸附测定)法检测 vero-E6,细胞培养上清正常标本 10 份的结果(100XOD490值)为 2,3,3,4,4,5,5,5,6,8,求标准差。
若用式(4.16)则先计算
∑X=2+3+3+…+6+8=45
∑X2=22+32+32+…62+82=229
若用式(4.17)则先计算
∑fX=1×2+2×3+…+1×6+1×8=45
∑fX2=1×22+2×32+…1×62+1×82=229
然后代入式(4.16)或式(1.17)结果相同。
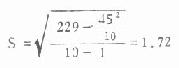
三、变异系数
上述各种变异指标可用来比较同类事物变量值间的变异情况。各变异指标的共同点是:值小表示变量值密集,值大表示变量值分散。但在有些情况下用标准差等变异指标来比较就不适宜了。如某地 7 岁男童身高均数为 123.10cm,标准差为 4.71cm; 体重的均数为 22.29kg,标准差为 2.26kg。由于单位不同,我们不能因为 4.71>2.26 而说身高的变异大于体重,需要有另一个指标,它不受单位的限制,那就是变异系数,其公式为:
CV=S/X×100%,X>0(4.18)
也就是将标准差化为各自均数的百分数,然后比较。这样不但可以比较单位不同的变量值间的变异,而且可以比较均数相差悬殊的变量值间的变异。
上述 7 岁男童身高、体重的变异系数分别为
身高 CV=4.17/123.10×100%=3.83%
体重 CV=2.26/22.29×100%=10.14%
可见同一批儿童的体重变异比身高的大。
例 4.12 被试者 9 人,试验时坐在舒适的牙科椅上测口腔压力波幅 PcmAq(厘米水柱)。然后外加呼吸阻力 20cmAq(1/sec),5 分钟时再测口腔压力波幅结果如下。试比较外加呼吸阻力前后,口腔压力波幅的变异。
表 4.9 外加呼吸阻力前后的口腔压力波幅
口腔压力波幅,cmAg
| 口腔压力波幅,cmAg | |||
| X | S | CV(%) | |
| 加阻力前 | 1.218 | 0.256 | 21.019 |
| 加阻力后 | 7.240 | 0.633 | 8.741 |
外阻力前口腔压力波幅的变异较大。
外加呼吸阻力前后的口腔压力波幅的单位都是 cmAq,如直接比较两个标准差,可能会得出加阻力后数值变异较大的结论。但由于两均数相差悬殊,加阻力后的均数几乎是加阻力前的 6 倍,因此就不宜直接比较标准差而应比较它们的变异系数。
变异系数还常用于比较多个样品重复测定的误差等。
运用变异系数时应注意(1)有关的事物间才能作比较,不要将风马牛不相及的东西硬拉在一起作比较;(2)均数小于标准差时应考虑其实际运用价值。因为在这种情况下,可能誇大变异,故不宜使用;(3)比较两变异系数间是否真有差别,亦应作假设检验,不能只看表面值就下结论。
[附]比较两变异系数可用 u 检验,其公式为
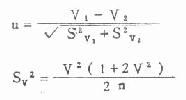
式中 V 为以小数表示的变异系数,SV2是变异系数的标准误的平方,n 是样本含量。u 是正态离差系数。
例 4.13 比较例 4.12 中两总体变异系数间有无差别。
H:两总体变异系数相等
H1:两总体变异系数不等
α=0.05

u>u0.05,0.05>P>0.01, 在 α =0.05 的水准处拒绝 H,接受 H 1,两总体变异系数不等。外加呼吸阻力前的口腔压力波幅的变异较大。
四、运用变异指标的注意事项
1.变异指标表示变量值的变异情况或离中趋势,常与位置指标平均数结合运用,说明变量值集中的位置与离散程度。
2.变异指标种类虽多,但任一变异指标,其值大表示变异大,数值参差甚;值小表示变异小,数值较集中。比较两个或几个同类事物的变异,要用同一变异指标。
3.正态分布资料宜用均数与标准差(有时用方差)描述集中与离散情况,记为 X±S。有了均数与标准差就可根据正态分布理论将频数分布描绘出来,进一步可作正常值范围估计与假设检验等(详见第五至第七章),应用较广。为便于计算,正态分布资料亦可用中位数、百分位数和四分位数间距等描述,其结果与用均数、标准差相近。
偏态分布资料宜用中位数及四分位数间距、均差等描述。尤其在资料分布呈明显偏态时,随着例数的增多,中位数、四分位数间距及均差的代表性和稳定性明显优于均数、标准差及方差。
众数和极差只用来对单峰资料作概括的描述。
4. 比较几组资料的变异程度,若各组资料的单位不全相同,或均数相差悬殊时,用变异系数。
5.判断几个方差或变异系数间有无显著差别,需作假设检验,不能只看表面值。详见第七、第八章有关内容。
练习题
1.
| 19.0 | 12.0 | 14.0 | 14.0 | 8.2 | 13.0 | 6.5 | 12.0 | 15.0 | 17.2 |
| 12.0 | 12.7 | 25.0 | 8.5 | 20.0 | 17.0 | 8.4 | 8.0 | 13.0 | 15.0 |
| 20.0 | 13.0 | 13.0 | 14.0 | 15.0 | 7.9 | 10.5 | 9.5 | 10.0 | 12.0 |
| 6.5 | 11.0 | 12.5 | 7.5 | 14.5 | 17.5 | 12.0 | 10.0 | 11.0 | 11.5 |
| 16.0 | 13.0 | 10.5 | 11.0 | 14.0 | 7.5 | 14.0 | 11.4 | 9.0 | 11.1 |
| 10.0 | 10.5 | 8.0 | 12.0 | 11.5 | 19.0 | 10.0 | 9.0 | 19.0 | 10.0 |
| 22.0 | 9.0 | 12.0 | 8.0 | 14.0 | 10.0 | 11.5 | 11.0 | 15.0 | 16.0 |
| 8.0 | 15.0 | 9.9 | 8.5 | 12.5 | 9.6 | 18.5 | 11.0 | 12.0 | 12.0 |
2.测得某地 300 名正常人尿汞值,其频数表如下。试计算均数、中位数、何者代表性较好。
300 例正常人尿汞值(μg/l)频数表
| 尿汞值 | 例 数 | 尿汞值 | 例 数 | 尿汞值 | 例 数 |
| 0- | 49 | 24- | 16 | 48- | 3 |
| 4- | 27 | 28- | 9 | 52- | — |
| 8- | 58 | 32- | 9 | 56- | 2 |
| 12- | 50 | 36- | 4 | 60- | — |
| 16- | 45 | 40- | 5 | 64- | — |
| 20- | 22 | 44- | — | 68- | 1 |
3.将表 4.4 资料分别用 0.5cm、2cm 为组距编制频数表,并与表 4.3 的频数分布进行比较,你认为何者显示变量值分布的特征较好?
4.有 5 个变量值 7、9、10、14、15,试计算 X 及∑(X-x)。
5.下表为 10 例垂体催乳素微腺瘤经蝶手术前后的血催乳素浓度,试分别求术前、术后的均数,标准差及变异系数。应以何指标比较手术前后数据的变异情况?能说手术前数据的变异大吗?为什么?
手术前后患者血催乳素浓度(mg/ml)
| 例号 | 血催乳素浓度 | 例号 | 血催乳素浓度 | ||
| 术 前 | 术 后 | 术 前 | 术 后 | ||
| 1 | 276 | 41 | 6 | 266 | 43 |
| 2 | 880 | 110 | 7 | 500 | 25 |
| 3 | 1600 | 280 | 8 | 1700 | 300 |
| 4 | 324 | 61 | 9 | 500 | 215 |
| 5 | 398 | 105 | 10 | 220 | 92 |
(资料来源:中华医学杂志,63(12)P730,1983
6.某地微丝蚴血症者 42 例治疗后 7 年用间接荧光抗体试验测得抗体滴度如下。求平均滴度。
| 抗体滴度的倒数 | 10 | 20 | 40 | 80 | 180 |
| 例 数 | 5 | 12 | 13 | 7 | 5 |
(资料来源:中华预防医学杂志:17(1),P22,1983)
第四章 正态分布与正常值范围估计
第一节 正态分布及其性质
一群变量值可能用平均数描述集中的位置,用变异指标描述离散情况,而频数表则把变量值的分布描绘得更具体。为了直观还可把频数表画成直方图。如第四章中曾将 7 岁男童坐高的频数分布绘成图 4.1。从图中可看出数据集中均数周围,左右基本对称,离均数愈近数据愈多,离均数愈远数据愈少的特点。医学科研中如健康人的红细胞数、血红蛋白量、血清总胆固醇,同年龄同性别儿童的身高、体重等,虽然数据各异,但画出的直方图图形是类似的。可以设想,这种类型的资料,如果调查例数无限增多,所用组距又无限的小,那么直方顶端就连成了一条光滑的曲线。这条曲线,典型地反映了这类资料的分布情况,数学上称为正态曲线,其方程为
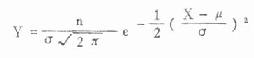
式中 n 为总频数,X 为变量值,μ 为均数,σ 为标准差,Y 为纵高,e=2.71828……,π=3.14158……。在一个总体中 n、μ、σ、e、π 都是常数,只有 X 在变,所以 Y =f(x)。
式(5.1)亦可写成:
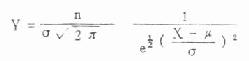
由上式可看出曲线的性质:
1.曲线左右对称。X- μ 无论是正或负,只要绝对值就相等,Y 值就相等。所以只要 X 与 μ 的距离相等,Y 就相等。Y 值以 X = μ 为对称轴。
2.中位数、均数、众数重合。正态曲线在横轴上方。当 X = μ 时,e=1,Y 为极大,所以均数与众数密合。由于曲线左右对称,所以均数亦即中位数。e 的指数愈大,Y 愈小,但不会得负值,所以 Y >0,曲线在横轴上方。
3.随着(X-μ/σ)的绝对值的增加,曲线由平均数所在点向左右两方迅速下降。
4.离平均数左右 1σ 处为曲线拐点。在 μ±σ 以内曲线向下弯曲,以外则向上弯曲。
这种类型的资料,数据值虽各不相同,但都有其均数与标准差,如果横轴上各以其均数为原点,标准差为单位,并令 x =X-μ,那么(X-μ)/ σ 可写成 x /σ,称为正态离差 u,
![]() (5.2)
(5.2)
再令总频数为 1。这时曲线以 μ 为原点,以 σ 为单位,称为标准正态曲线,其公式为
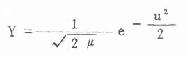 (5.3)
(5.3)
以 μ 为均数,σ2为方差的正态分布可记为 N(μ,σ2),因此标准正态分布可记为 N(0,1)。
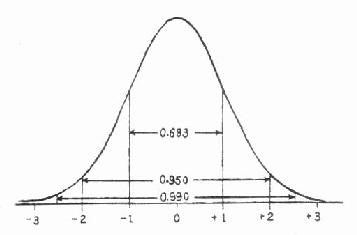
图 5.2 标准正态曲线
第二节 正态曲线下面积
直方图是以直方的面积表示数量的。直方顶端连成曲线后,整个曲线下面积就表示总频数,用 1 或 100% 表示。一定区间曲线下面积就是出现在此区间的频数与总频数之比,或出现在该区间的各个变量的概率之和。例如以 7 岁男童 102 人为 100%,则若要知道坐高在 66 至 68cm 间的人数占总人数的百分比,只要知道曲线下横坐标为 66 至 68cm 区间内的面积就可以了。因此求出曲线下面积有其实用意义。
曲线下某区间的面积,可根据曲线方程用积分求得,但若每次应用时都要用积分计算,那是很麻烦的。前人已将标准正态曲线下 0 至各 u 值的面积计算出来的了。由于各书列的方式不完全相同,所以使用时要注意表上的图示或说明,仍用 7 岁男童坐高资料为例说明正态曲线下面积表(附表 2)的使用方法。该表左侧及上端为 u 值,表中数字为横轴自 0 至 u 曲线下的面积。
例 5.1 根据表 4.3 的资料计算得坐高的 X =66.72,S=2.08,试估计总体中坐高在
(1)66.72-68.80cm 间。
(2)66~68cm 间及(3)68~70cm 间的人数各占总人数的百分比。
(1)求坐高在 66.72~68.80cm 之间曲线下面积。
①求 u(u=(X-μ)/σ,这里分别以 X、S 作为 μ 与 σ 的估计值)
(66.72-66.72)/2.08=0
(66.80-66.72)/2.80=1
标准正态曲线下面积见图 5.3(a)。
②查附表 2,u 自 0 至 1 的面积,即查 u =1.00,得 α /2=0.3413。坐高在此区间内的人数占总人数的 34.13%。
(2)求坐高在 66~68cm 之间曲线下面积。
①求 u
(66-66.72)/2.08=-0.346
(68-66.72)/2.08=0.615
标准正态曲线下面积见图 5.3(b)
②查附表 2 u=0.346,得 α /2=0.1353(经内插法求得,下同)
u=0.615,得 α /2=0.2308
0.1353+0.2308=0.3661
坐高在此区间内的人数占总人数的 36.61%,即 102×0.3661=37.3 人,与实际观察所得 38 人相近。
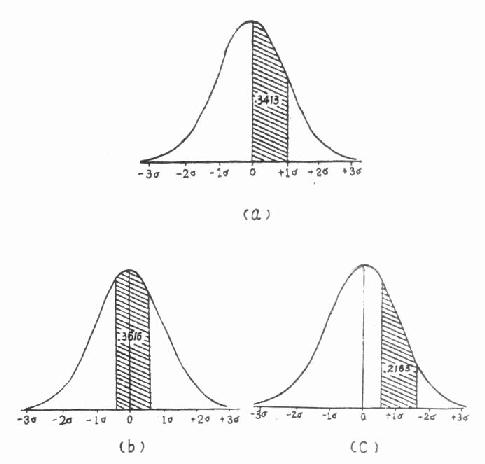
图 5.3 正态曲线下面积之计算
(3)求坐高在 68~70cm 间的人数占总人数的百分比。
①求 u
(68-66.72)/2.08=0.615
(70-66.72)/2.08=1.577
标准正态曲线下面积见图 5.3(c)
②查附表 2,u=1.577, 得 α /2=0.4426
u=0.615, 得 α /2=0.2308
0.4426-0.2308=0.2118
坐高在此区间内的人数点总人数的 21.18%,即有 102×0.2118=21.6 人。与实际观察所得 20 人相近。
从例 5.1 可见,因为正态曲线对称于原点,所以不论 u 为正还是负,绝对值相同时,自 0 至 u 的面积相同。查附表 2 时,若两个 u 值中有一个是 0,按另一 u 值查得 α /2;若两个 u 异号,将查出的两个 α / 2 值相加;若两个 u 同号,则将大的 α / 2 值减去小的即得。但不能将两个 u 值相加(或减)后再查面积。
例 5.1 已求得 u 从 0 - 1 时,α/2=0.3413, 所以 u 从 -1~1,曲线下面积为 0.6827,说明有 68.27% 的变量值在 μ±σ 的范围内(见图 5.2)。查附表 2,当 u =1.96 时,α/2=0.475,因此 μ±1.96σ 的范围内包含有 95% 的变量值,只有 5% 的变量值在此范围外。由于曲线左右对称,因此有 2.5% 的变量值等于或小于 μ -1.96σ;2.5% 变量值等于或大于 μ +1.96σ。同理,查附表 2,u=2.58 时,α/2=0.495, 因此 μ±2.58σ 范围内有 99% 的变量值,在此范围外的仅占 1%。u=1.96 和 u =2.58(准确说是 u =2.5758)是正态分布中两个重要的界值,称 5% 界和 1% 界,今后在正常值范围估计、假设检验等中常常要用到。
如果已知资料呈正态分布,那么理论上只要知道 μ 和 σ 就可根据曲线下面积表求出任两值之间变量值的个数,也就是说能算出变量值的频数分配。但实际上 μ 和 σ 常常无法获得,因此只能用 X 和 S 作为 μ 和 σ 的估计值,来估计总
体中变量值(个体值)的分布。
第三节 正常值范围的估计
在医学科研中有时需要根据样本数据推论总体中个体值范围,其中最常用的是估计正常值范围。
一、正常值范围的意义
正常人体的解剖、生理、生化、心理等各种数据的波动范围称正常值范围,简称正常值。如成人白细胞总数的正常值为 4000~10000 个 /mm3。以一定数量“正常人”为样本,观察某个或几个变量,根据所得样本数据,推论总体中变量值的范围,称正常值范围估计。一些与人体有关的外界环境如噪音强度、粉尘浓度、昆虫密度、水中微量元素的含量等,在某一地域、某段时期内亦在一定范围内波动;某病患者在病程的某段时期内,某种检验结果亦常在一定范围内波动。虽然这些范围不一定是正常的,有的超过了卫生标准或正常值,但若从样本数据估计总体中变量值的范围来说,那么也可以用本章的估计方法,得出的波动范围可称为个体值范围。
二、确定正常值范围的一般原则和步骤
1.确定研究总体。即对研究总体的同质性基础作出规定。以“正常人”为例,所谓正常人不是指任何组织与器官的形态及机能都无异常的人,而是指排除了影响被研究指标的疾病和有关因素的人。例如某单位研究血清谷一丙转氨酶活性的正常值,选取“正常人”的条件为无肝、肾、心、脑、肌肉等器质性疾患,近期无特殊用药史(如氯丙嗪、异烟肼等),测定前未作剧烈运动等。上述条件就是保证研究对象的同质性作出的规定。但不允许以所研究指标值的大小来划分是否“正常人”。对研究总体,如“正常人”的规定要根据研究目的、技术力量与水平以及人力物力等条件来考虑,往往牵涉到多方面的专业知识。但一般可从地区、民族、性别、年龄、劳动条件(如是否与有害物质接触)、时间(季节与昼夜)、月经、妊娠、饮食、药物、生活习惯等来考虑。例如红细胞数及血红蛋白量,高原居民与平原不同,男子各异;人体血清胆固醇含量随年龄的增长而增加,妊娠期高于非妊娠期,冬季高于夏季,且受饮食影响;服用某些药物可直接增加检测的有关成分或干扰检测结果的准确性。
各种影响因素,有些可通过询问与体检严格控制,如排除那些与被研究指标有关的各病患者,或处于妊娠、经期的妇女,近期内服用某种药物者等;有些可用对调查资料分组统计的办法加以控制或研究。如先按男、女分别统计,然后检验两组数据的分布、均数与标准差等,有无差别,若有差别则分别求正常值,否则可合并求通用的正常值。
2.确定观察例数。正常值范围的影响因素复杂,要使样本分布能正确估计总体分布,例数不能太少,一般认为应在 200 例左右。数据变异不大,观测比较精确的,例数可相应少些;影响因素复杂、数据变异大,观测方法不够稳定的,例数相应要多一些。但要防止片面追求数量,而抽选样本不按规定,观测方法不统一,粗率马虎,以致影响原始数据的可靠性。
3.统一测定方法,控制实验误差,保证数据的可靠性。为达到上述要求应注意对检测人员(医生、检验人员等)的培训,以统一认识、统一方法和操作,标准化仪器和试剂,建立质量控制防止记录差错等。但也要尽量与应用正常值范围时的实际情况相一致,例如临床检验每一个标本只作一次,那么为确定正常值的检验每个标本亦只作一次,不能作两个平行样本求平均数后再估计正常值。否则可能定出的正常值范围较窄。
4.确定取单侧还是双侧界值。某些指标如白细胞总数,无论过低或过高都不正常,因此需要确定下限和上限两个界值,称双侧界值。有的指标如肺活量一般只认为过低是不正常,所以只需定下测界值,即下限;但血铅只是过高不正常,只需定上限。只需定下限或上限的,称单侧界值。确定取单侧还是双侧界值,应根据业务知识与指标用途。
5.确定适当的百分范围。调查一定数量的正常人若以某指标的最小、最大值作为正常值范围,常因调查例数的增加等遇到少数极端值,使正常值范围不稳定。因此统计上常采用一些方法,删去一定比例的极端值,使得出的正常值能较稳定地反映绝大多数正常人该指标的数值。那么绝大多数是指正常人的百分之多少呢?一般包括正常人的 80%、90%、95% 或 99% 等。这样,若按单侧计算,相应地将有 20%、10%、5% 或 1% 的正常人该指标值在正常值范围以外;若按双侧计算,相应地,过高、过低者各有 10%、5%、2.5% 或 0.5%。这些指标值在正常值范围以外的正常人,将被错判为不正常。将正常错判为不正常,称为 I 型错误,或假阳性,其假阳性率或误诊率用 α 表示。但亦有些病人的指标值,可能落在正常值范围以内,这时就会将病人错判为正常人,这种错判Ⅱ型错误,或假阴性,假阴性率即漏诊率用 β 表示。确定合适的百分范围应根据研究目的,结合正常人和病人的数值分布,同时考虑 α 及 β,一般有下列两种情况:
(1)正常人和病人的数据分布无重叠(见图 5.4a)。这时只考虑减少 α;
(2)正常人和病人的数据分布有重叠(见图 5.4b)。这时两分布重叠部分内既有病人亦有正常人,若欲减少 α,界值向右移,那么 β 将加大;若欲减少 β,界值向左移,那么 α 将加大。通常兼顾 α 及 β,取两曲线交点的横座标为界值,这时 α 与 β 之和为最小。但实用时还要考虑该正常值范围的主要用途,若用以普查初筛病人,则要减少假阴性,取 80% 或 90% 正常值范围;若用以确诊病人,则要避免假阳性,以取 95% 或 99% 正常值范围为宜。
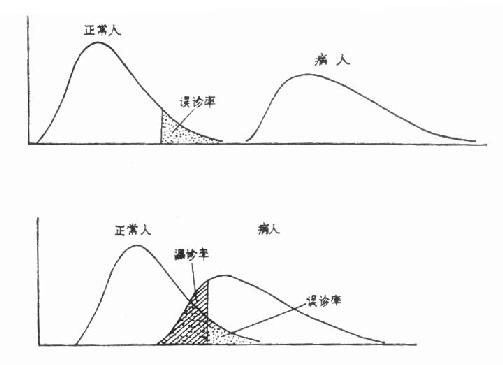
图 5.4 正常人和病人数据分布示意图
6.确定估计方法进行估计。估计正常值范围的方法较多,主要根据频数的分布类型和样本含量选用。常用的有百分位数法和正态分布法。运用百分位数法的条件是样本含量大,适用正态分布法的条件是资料服从正态分布或经过转换后服从正态分布。此外尚有曲线拟合法等。
三、确定正常值范围的方法
1.百分位数法。本法根据正常人样本数据,按照选定的百分范围计算相应的百分位数作为正常值范围的界值。可根据原始数据直接计算,亦可根据频数表进行计算。计算步骤为:
(1)按已确定的百分范围从表 5.1 查得应计算的百分位数;
(2)计算出各百分位数的所在位置;
(3)代入公式计算界限 P x
表 5.1 估计正常值范围的计算项目
| 百分范围(%) | 百分位数法 | 正态分布法 | ||
| 双侧 | 单侧下 (或上) 限 | 双侧 | 单侧下 (或上) 限 | |
| 80 | P10及 P 90 | P20(或 P 80) | X±1.282S | X-(或 +)0.842S |
| 90 | P5及 P 95 | P10(或 P 90) | X±1.645S | X-(或 +)1.282S |
| 95 | P2.5及 P 97.5 | P5(或 P 95) | X±1.960S | X-(或 +)1.645S |
| 98 | P1及 P 99 | P2(或 P 98) | X±2.326S | X-(或 +)2.054S |
| 99 | P0.5及 P 99.5 | P1(或 P 99) | X±2.576S | X-(或 +)2.326S |
例 5.2 某地测得 200 例健康成人的血铅值(微克 /100 克)得频数分布如下,试估计单侧 95% 上限。
(1)查表 5.1,百分范围 95,百分位数法,单侧上限应求 P 95。
(2)求 P 95的位置 200×0.95=190 即为第 190 个数据处,因此知 A =188,Lx=35,fx=4,ix=5。
代入公式(4.5)
表 5.2 百分位数法计算单侧上限(200 例健康成人的血铅值)
| 血铅值(微克 /100 克) | 频数 | 累计频数 |
| 0- | 6 | 6 |
| 5- | 48 | 54 |
| 10- | 43 | 97 |
| 15- | 36 | 133 |
| 20- | 28 | 161 |
| 25- | 13 | 174 |
| 30- | 14 | 188 |
| 35- | 4 | 192 |
| 40- | 4 | 196 |
| 45- | 1 | 197 |
| 50- | 2 | 199 |
| 55- | 199 | |
| 60- | 1 | 200 |
| 合计 | 200 | – |
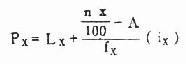
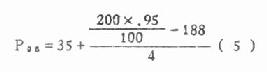
健康成人血铅值的 95% 正常值上限为 37.5 微克 /100 克。
若根据原始资料计算,已算得 Px 的位置为第 190 个数据后,将原始数据从大至小排,第 10 个数据的值即为 Px。
此法的优点是不拘资料的分布类型,计算简便,样本含量较大,分布较稳定时结果稳定。但估计结果受样本极差的限制,受两侧尾部数据的影响较大,尤其是百分范围较大(如大于 95%)。样本含量不够在时,结果不够稳定。
2.正态分布法。正态分布法运用正态曲线下面积与 μ±μα σ 的关系来估计数值范围的。在图 5.2 中曾提到 μ±1.96σ 的范围内包含了曲线下总面积的 95%,亦就是总例数的 95%。在此范围外则有 2.5% 的例数其数据值大于 μ±1.96σ, 另 2.5% 小于 μ -1.96σ。因此,就可用 μ±1.96σ 来估计双侧 95% 的正常值范围。同理可用 μ 与相应的 μ ασ 估计所需百分范围,μ 可从附表 2 查得。但在实际中 μ 与 σ 常常是不知道的,只能用它们的估计值 X 与 S
来代替。估计正常值范围时常用的百分范围与相应的 X±us 见表 5.1。用正态分布法估
计正常值范围的公式为
X±uαs(5.4)
例 5.3 测得西安市 7 岁男童 102 人坐高,X=66.72,S=2.08,试用正态分布法估计
双侧 95% 正常值范围。
查表 5.1,百分范围 95,正态分布法双侧,应求 X±1.96S。
代入公式(5.4)
66.72±1.96×2.08=(62.6432,70.7968)
西安市 7 岁男童坐高的 95% 正常值范围为 62.6~70.08 公分。
此法适用于正态分布资料,样本均数和标准差比较稳定者,其优点是结果稳定,受两端尾部数据影响较小,也不受样本数据极差的限制,缺点是只适用于正态分布资料。医学上不少资料呈偏态分布,但计算较繁。
练习题
1.
2.调查得成都市 1979 年 996 名女学生月经初潮年龄的分布如下,本资料宜用何法确定其双侧 99% 正常值范围?试估计之。
| 年岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 合计 |
| 人数 | 7 | 44 | 153 | 244 | 269 | 191 | 61 | 16 | 8 | 1 | 2 | 996 |
3.某市 20 岁男学生 160 人的脉搏数(次 / 分钟),经正态性检验服从正态分布。求得 X =76.1,S=9.32,试估计脉搏数的 95%、99% 正常值范围。
4.已知 238 例正常人发汞值(μg/g)的最后 14 个发汞值如下,求 95% 单侧上限。
| 发汞值…… | 2.6 | 2.6 | 2.6 | 2.6 | 2.7 | 2.7 | 2.7 | 2.8 | 2.8 | 3.0 | 3.3 | 4.0 | 4.1 | 4.3 |
| 秩次…… | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 |
第五章 标准误与可信区间
第一节 抽样误差与标准误
一、抽样误差的意义
在第一章第二节曾提到过样本与总体以及抽样误差的概念,那里谈到,由于存在人与人之间的个体差异,即使从同一总体用同样方法随机抽取例数相同的一些样本,各样本算得的某种指标,如平均数(或率),通常也参差不齐存在一定的差异。样本指标与相应的总体指标之间有或多或少的相差,这一点是不难理解的。如某医生从某地抽了 120 名 12 岁男孩,测量其身高,计算出均数为 143.10cm,若再从该地抽 120 名 12 岁男孩,其平均身高未必仍等于 143.10cm,也不一定恰好等于某市 12 岁男孩身高的总体均数,这种差异,即由于抽样而带来的样本与总体间的误差,统计上叫抽样波动或抽样误差。
抽样误差和系统误差不一样,关系系统误差,当人们一旦发现它之后,是可能找到产生原因而采取一定措施加以纠正的,抽样误差则无法避免。因为客观上既然存在个体差异,那么刚巧这一样本中多抽到几例数值大些的,所求样本均数就会稍大,另一样本多抽到几例数值小些,该样本均数就会稍小,这是不言而喻的。
抽样误差既是样本指标与总体指标之间的误差,那么抽样误差小就表示从样本算得的平均数或率与总体的较接近,有样本代表总体说明其特征的可靠性亦大。但是,通常总体均数或总体率我们并不知道,所以抽样误差的数量大小,不能直观地加以说明,只能通过抽样实验来了解抽样误差的规律性。
二、标准误及其计算
为了表示个体差异的大小,或者说表示某一变量变异程度的大小,可计算标准差等变异指标来说明,现在我们要表示抽样误差的大小,如要问,从同一总体抽取类似的许多样本,各样本均数(或各率)之间的变异程度如何?也可用变异指标来说明。这种指标是:
(一)均数的标准误 为了表示均数的抽样误差大小如何,用的一种指标称为均数的标准误。我们以样本均数为变量,求出它们的标准差即可表示其变异程度,所以将样本均数这“标准差”定名为均数的标准误,简称标准误,以区别于通常所说的标准差。标准差表示个体值的散布情形,而标准误则说明样本均数的参差情况,两者不能混淆。下面用抽样实验进一步说明之。
将 100 名正常人的红细胞数(万 /mm3)写在 100 颗大小均匀的豌豆上。这些红细胞数见表 6.1,其均数为 500,标准差为 43。把这些豌豆放在一个口袋里,彻底混匀后取出一颗,记下红细胞数,放回袋内,混匀后再取出一颗,记下数字后再放回去,如此继续下去,这是一个取不完的总体,这样每取 10 个数字作为一个样本,共抽取了一百个样本,并计算每一样本的均数与标准差,例见表 6.2。
表 6.1 红细胞数抽样实验用的正态总体
μ=500 σ=43(单位:万 / 立方厘米)
| 383 | 410 | 422 | 429 | 430 | 431 | 435 | 442 | 442 | 444 |
| 445 | 449 | 450 | 452 | 455 | 456 | 459 | 461 | 462 | 463 |
| 465 | 466 | 468 | 469 | 470 | 471 | 472 | 473 | 476 | 477 |
| 478 | 479 | 480 | 481 | 482 | 484 | 485 | 486 | 487 | 488 |
| 489 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 |
| 500 | 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 |
| 511 | 512 | 513 | 514 | 515 | 516 | 518 | 519 | 520 | 521 |
| 522 | 523 | 524 | 527 | 528 | 529 | 530 | 531 | 532 | 534 |
| 535 | 537 | 538 | 539 | 541 | 544 | 545 | 548 | 550 | 551 |
| 555 | 556 | 558 | 565 | 569 | 578 | 590 | 599 | 600 | 617 |
表 6.2 红细胞数抽样实验中的样本举例
| 样本号 | 红细胞数(万 / 立方毫米),X | X | S | |||||||||
| 1 | 383 | 599 | 534 | 442 | 435 | 486 | 478 | 476 | 509 | 544 | 488.6 | 61.65 |
| 2 | 503 | 506 | 520 | 503 | 489 | 410 | 528 | 488 | 509 | 527 | 498.3 | 33.97 |
| 3 | 478 | 463 | 617 | 544 | 498 | 485 | 496 | 462 | 482 | 569 | 509.4 | 50.96 |
| 4 | 529 | 465 | 535 | 473 | 531 | 532 | 556 | 521 | 459 | 383 | 498.4 | 52.63 |
| 5 | 442 | 493 | 462 | 527 | 520 | 519 | 521 | 512 | 482 | 471 | 494.9 | 29.51 |
| ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ | ┇ |
第一号样本均数与标准差的计算:
X=4.886/10=488.6
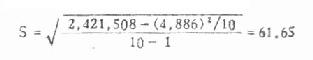
将一百个样本均数加总,得到的数值为 50,096.7, 又这一百个样本均数平方之和为 25,114,830.91,于是代入标准差的计算公式,求得一百个样本均数的标准差又称标准误为
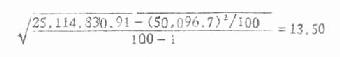
当总体标准差已知时,可计算理论的标准误 σ χ,公式是
![]() (6.1)
(6.1)
表 6.1 抽样实验用的总体标准差是 43,每个样本的例数是 10,代入公式得
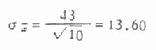
可见由一百个样本均数求得的标准误 13.50 与理论的标准误 13.60 比较接近。
在实际工作中,总体标准差往往并不知道,也不象抽样实验那样从同一总体随机抽取 n 相等的许多样本,而是只有手头一个样本。在此情况下,只能以样本标准差 S 作为总体标准差 σ 的估计值。这样,公式 6.1 中的 σ 就要用 S 代替,σχ改为 S χ,以资区别。
![]() (6.2)
(6.2)
将第 1 号样本的标准差及例数代入式 6.2,得
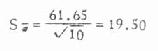
再若将第 2 号样本的数字代入,Sχ将成为 10.74,余类推。由于不同样本的标准差并不相等,可见 S χ也有抽样波动,这一点是值得注意的,但它仍不失为 σ χ的较好估计值。
以上介绍了求标准误的三种方法,其实我们平常用的只是式 6.2,而通过前两种方法的对比则可使我们明瞭标准误的含义。标准误是描述样本均数变异情况的一个指标,它的大小与总体标准差 σ(一般只能用 S 估计)成正比,而与样本含量 n 的平方根成反比,因此若标准差小或样本含量大时,求出的标准误就小(标准误小表示样本均数与总体均数较接近),X 代表 μ 较可靠,所以假若手头资料中观察值的变异程度较大(S 大)时,为了保
证样本代表总体比较可靠,就得适当增大样本含量(n)。
(二)率的标准误 若总体包括某事件的发生数与未发生数两类,所化成的比例或成数即为总体发生率(符号 π)与未发生率(1-π)。从总体中随机抽取许多样本(n 相等),算出各个样本率(用 P 表示),会是或大或小有波动的。为了表示样本率之间或样本率与总体率之间的差异程度,当总体率 π 已知时,可计算理论的标误 σ p, 其公式是
 (6.3)
(6.3)
实际工作中往往不知道总体率 π 这时只能以样本率 P 作为总体率 π 的估计值,求得率的标准误,并用 S P表示,计算公式为
![]() (6.4)
(6.4)
现举例说明其求法。
例 6.1 某医生检测了 110 名成年健康人的尿紫质,发现阳性者 11 人,阴性者 99 人,于是算得阳性率 P 及率的标准误 S P如下:
P=11/110×100%=10%(用小数表示为 0.10)
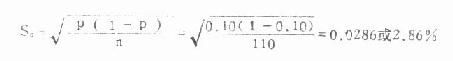
若要进一步增强样本率估计总体率的可靠性,可加大样本含量。
三、样本均数的分布
从同一总体里随机抽取 n 相同的许多样本,这些样本均数吴正态分布。如前面所述正常人红细胞数的抽样实验中已求得 100 个样本均数,其中多数与总体均数 μ 比较接近而集中分布在其周围,且左右基本对称,见表 6.3(此表由表 6.4 中的 100 个均数划记归组而得)。
表 6.3 红细胞抽样实验中 100 个样本均数的分布
| 组 段 | 460- | 470- | 480- | 490- | 500- | 510- | 520- | 530- | 540- | 合计 |
| 样本数 | 1 | 3 | 18 | 28 | 28 | 13 | 7 | 1 | 1 | 100 |
表 6.4 一百个样本的均数、标准差、95% 可信区间
| 样本号 | 均数 | 标准差 | 95% 可信区间 | 样本号 | 均数 | 标准差 | 95% 可信区间 | |
| 1 | 488.6 | 61.65 | 444.49~532.71 | 2 | 498.3 | 33.97 | 474.01~522.59 | |
| 3 | 509.4 | 50.96 | 472.96~545.84 | 4 | 498.4 | 52.63 | 460.76~536.04 | |
| 5 | 494.9 | 29.51 | 473.80~516.00 | 6 | °546.7 | 43.23 | 515.78~577.62* | |
| 7 | 524.5 | 33.60 | 500.45~548.55* | 8 | 488.3 | 41.04 | 458.94~517.66 | |
| 9 | 485.3 | 55.14 | 445.85~524.75 | 10 | 502.6 | 48.55 | 467.88~537.32 | |
| 11 | 495.1 | 40.63 | 466.03~524.17 | 12 | 524.7 | 37.81 | 497.65~551.75 | |
| 13 | 512.7 | 53.18 | 474.65~550.75 | 14 | 494.8 | 37.24 | 468.15~521.45 | |
| 15 | 493.6 | 39.94 | 465.03~522.17 | 16 | 495.3 | 29.47 | 474.22~516.38 | |
| 17 | 491.0 | 19.32 | 477.18~504.82 | 18 | 506.5 | 53.83 | 468.00~545.00 | |
| 19 | 487.5 | 39.39 | 461.32~517.68 | 20 | 495.9 | 32.70 | 472.51~519.29 | |
| 21 | 504.8 | 34.76 | 479.94~529.66 | 22 | 512.2 | 44.76 | 483.17~547.23 | |
| 23 | 496.5 | 40.65 | 467.41~525.59 | 24 | 499.8 | 37.04 | 473.31~526.29 | |
| 25 | 505.7 | 37.21 | 479.08~532.32 | 26 | 487.7 | 34.50 | 463.02~512.38 | |
| 27 | 501.5 | 37.35 | 474.79~528.21 | 28 | 476.1 | 29.64 | 454.91~497.29* | |
| 29 | 523.2 | 51.57 | 486.31~560.09 | 30 | 509.5 | 33.61 | 485.45~533.55 | |
| 31 | 494.2 | 28.60 | 473.75~514.65 | 32 | 506.2 | 25.29 | 483.10~524.30 | |
| 33 | 501.1 | 27.88 | 481.15~521.05 | 34 | 520.6 | 30.23 | 498.98~542.22 | |
| 35 | 492.0 | 42.18 | 461.82~522.18 | 36 | 509.6 | 19.17 | 495.89~523.31 | |
| 37 | 488.6 | 42.29 | 458.36~518.84 | 38 | 510.9 | 47.55 | 476.88~544.92 | |
| 39 | 516.4 | 39.96 | 487.81~544.99 | 40 | 518.8 | 46.43 | 485.59~552.01 | |
| 41 | 495.9 | 36.89 | 469.53~522.27 | 42 | °526.4 | 42.78 | 495.80~557.00 | |
| 43 | 505.8 | 53.84 | 467.30~544.30 | 44 | 503.0 | 47.33 | 469.14~536.86 | |
| 45 | 504.8 | 47.77 | 470.62~538.98 | 46 | 492.4 | 29.20 | 471.52~513.28 | |
| 47 | 505.5 | 38.32 | 478.08~532.92 | 48 | 486.5 | 52.98 | 448.59~524.41 | |
| 49 | 515.2 | 38.69 | 487.51~542.89 | 50 | 487.0 | 53.75 | 448.55~525.45 | |
| 51 | 503.3 | 51.54 | 466.43~540.17 | 52 | 491.0 | 58.47 | 449.18~532.82 | |
| 53 | 522.3 | 65.01 | 475.79~568.81 | 54 | 490.3 | 49.92 | 454.58~526.02 | |
| 55 | 516.7 | 37.26 | 490.05~543.35 | 56 | 489.6 | 31.41 | 467.14~512.06 | |
| 57 | 490.0 | 62.90 | 445.01~534.99 | 58 | 489.2 | 30.91 | 467.09~511.31 | |
| 59 | 509.1 | 40.51 | 480.12~538.08 | 60 | 513.5 | 29.18 | 492.62~534.38 | |
| 61 | 476.4 | 42.06 | 446.32~506.48 | 62 | 511.5 | 28.46 | 491.14~531.86 | |
| 63 | 480.7 | 44.83 | 448.62~512.78 | 64 | 501.4 | 29.00 | 480.66~522.14 | |
| 65 | 481.1 | 50.65 | 444.86~517.34 | 66 | 496.0 | 36.53 | 469.87~522.13 | |
| 67 | 489.2 | 44.20 | 457.58~520.82 | 68 | 494.8 | 29.73 | 473.54~516.06 | |
| 69 | 497.2 | 68.49 | 448.21~546.19 | 70 | 504.1 | 35.13 | 478.95~529.25 | |
| 71 | 507.9 | 34.35 | 483.33~532.47 | 72 | °465.3 | 25.56 | 447.02~483.58* | |
| 73 | 502.6 | 45.54 | 470.03~535.17 | 74 | 486.4 | 48.51 | 451.70~521.10 | |
| 75 | °526.6 | 32.68 | 503.10~550.10* | 76 | 503.2 | 47.18 | 469.45~536.95 | |
| 77 | 496.7 | 33.45 | 472.77~520.63 | 78 | 504.8 | 43.52 | 473.67~535.93 | |
| 79 | 490.2 | 58.07 | 448.67~531.73 | 80 | 486.6 | 26.60 | 467.57~505.63 | |
| 81 | 506.1 | 28.48 | 485.72~526.48 | 82 | 513.7 | 29.28 | 492.75~534.65 | |
| 83 | 481.5 | 29.78 | 460.19~502.81 | 84 | 491.2 | 44.73 | 459.22~523.18 | |
| 85 | 515.7 | 25.78 | 497.26~534.14 | 86 | 513.9 | 64.62 | 467.69~560.11 | |
| 87 | 496.4 | 23.82 | 479.37~513.43 | 88 | 507.4 | 45.14 | 475.10~539.70 | |
| 89 | 479.1 | 44.15 | 465.52~528.68 | 90 | 498.9 | 30.16 | 477.32~520.48 | |
| 91 | 503.7 | 53.90 | 465.16~542.24 | 92 | 495.9 | 30.86 | 473.78~518.02 | |
| 93 | 494.6 | 58.48 | 452.78~536.42 | 94 | 507.1 | 42.44 | 476.74~537.46 | |
| 95 | 488.5 | 36.15 | 462.65~514.35 | 96 | 489.1 | 68.01 | 440.44~537.76 | |
| 97 | °530.1 | 58.72 | 488.09~572.11 | 98 | 518.7 | 45.10 | 486.44~550.96 | |
| 99 | 507.8 | 41.87 | 477.85~537.73 | 100 | 540.6 | 55.17 | 465.13~544.07 | |
已知按正态分布,理论上有 95% 的变量值分布在均数加、减 1.96 倍标准差(样本均数的标准差称标准误)的范围内,这里也即 100 个样本均数中有 95 个分布在 500-1.96(13.60)=473.34 至 500+1.96(13.60)=526.66 的范围内。现看表 6.4,在 100 个样本均数中,第 6 号(546.7)、第 72 号(465.3)、第 97 号 (530.1) 在上述范围之外,第 42 号 (526.4) 及第 75 号 (526.6) 就在临界值附近,其余 95 个(若将第 42 及 75 号计算在内则为 97 个)样本均数在此范围之内,将实际分布与理论分布相对照见下表 6.5。100 个样本均数的实际分布与正态分布的理论基本符合。
第二节 t 分布
从数理统计的理论上讲,并且上节的实例也已说明,在总体均数为 μ,总体标准差为 σ 的正态总体中随机抽取 n 相等的许多样本,分别算出样本均数,这些样本均数呈正态分布。而当样本含量 n 不太小时,即使总体不呈正态分布,样本均数的分布也接近正态。在下式中,
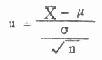
由于 μ 与(样本均数的标准差)都是常量,又
X 呈正态分布,所以 u
也呈正态分布。但实际上总体标准差往往是不知道的,上式分母中的 σ 要由 S 替代,成为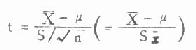 ,那么由于样本标
,那么由于样本标
准差有抽样波动,SX 也有抽样波动,于是,在用 S 代替 σ
后上式等号右边的变量便不呈正态分布而呈 t 分布,其定义公式是
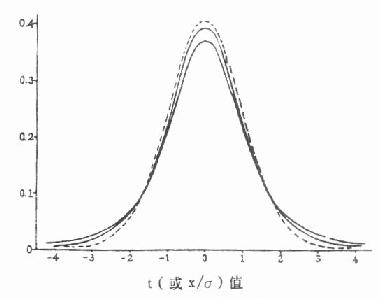 (6.5)
(6.5)
t 分布也是左右对称,但在总体均数附近的面积较正态分布的少些,两端尾部的面积则比正态分布的多些。t 分布曲线随自由度而不同(如图 6.1)。随着自由度的增大,t 分布逐渐接近正态分布,当自由度为无限大时,t 分布成为正态分布。

图 6.1 t 分布(实线)与正态分布(虚线)
与正态分布相似,我们把 t 分布左右两端尾部面积之和 α =0.05(即每侧尾部面积为 0.025)相应的 t 值称为 5% 界,符号为 t 0.05,,,这里 ν 是自由度。把左右两端尾部面积之和 α 为 0.01 相应的 t 值称为 1% 界,符号为 t 0.01,,。t 的 5% 界与 1% 界可查附表 3,t 值表。例如当自由度为 10-1= 9 时,t0.05,9=2.262,t0.01,9=3.250。
第三节 可信区间的估计
一、参数估计的意义
一组调查或实验数据,如果是计量资料可求得平均数,标准差等统计指标,如果是计数资料则求百分率藉以概括说明这群观察数据的特征,故称特征值。由于样本特征值是通过统计求得的,所以又称为统计量以区别于总体特征值。总体特征值一般称为参数(总体量)。我们进行科研所要探索的是总体特征值即总体参数,而我们得到的却是样本统计量,用样本统计量估计或推论总体参数的过程叫参数估计。
本章第一节例 6.1 通过检查 110 个健康成人的尿紫质算得阳性率为 10%,这是样本率,可用它来估计总体率,说明健康成人的尿紫质阳性率水平,这样的估计叫“点估计”。但由于存在抽样误差,不同样本(如再检查 110 人)可能得到不同的估计值。因此我们常用“区间估计”总体率(或总体均数)大概在那一个范围内,这个范围就叫可信区间。区间小的一端叫下限,大的一端叫上限。常用的有 95% 可信区间与 99% 可信区间。根据同一资料所作 95% 可信区间比 99% 可信区间窄些(上、下限较靠近),但估计错误的概率后者为 1%,前者为 5%,进行总体参数的区间估计时可根据研究目的与标准误的大小选用 95%、或 99%。
二、总体均数的估计
为了说明常用的总体均数之区间估计法,我们不妨回顾一下上节所叙的 t 分布。
由求 t 的基本公式
![]()
我们看到 X 与 μ 的距离等于 t(SX),又根据 X 集中分布在 μ 周围的特点,若取 t 的 5%
界即 t0.05,,(或 1% 界)乘以 SX 作为 X 与 μ 的距离范围,就可用式(6.6)或式 (6.7) 求
出区间来估计总体均数 μ 所在范围,估错的概率仅有 5% 或 1%,因此称 95% 或 99% 可信区间。下面用实例说明其求法。
95% 可信区间 X-t0.05,νSX<μ<x+t0.05,Νsx(6.6)< p=””></x+t0.05,Νsx(6.6)<>
99% 可信区间 X-t0.05,νSX<μ<x+t0.01,Νsx(6.7)< p=””></x+t0.01,Νsx(6.7)<>
例 6.2 上面抽样实验中第 1 号样本的均数为 488.6,标准差为 61.65,例数 10,自由度 ν =10-1=9,试求 95% 与 99% 可信区间。
1.求标准误
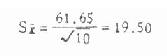
95% 可信区间 488.6-2.262(19.50)<μ<488.6+2.262(19.50), 即有 95% 的把握估计 μ 是在 444.49~532.71 区间内
99% 可信区间 488.6-3.250(19.50)<μ<488.6+3.250(19.50), 可有 99% 的把握估计 μ 是在 425.22~551.98 区间内
这里两个可信区间都包含 μ =500 在内,所以这次估计是估计对了。
抽样实验共抽了 100 个样本,除 1 号样本外其余 99 个样本均数也对 μ 作了区间估计,这些 95% 可信区间列在表 6.4 中。我们看到,只有 5 个 95% 可信区间(右上角标有星号)不包含总体均数 μ =500 在内,它们是:
| 样本号 | X | 95% 可信区间 |
| 6 | 546.7 | 515.78~577.62 |
| 7 | 524.5 | 500.45~548.55 |
| 28 | 476.1 | 454.91~497.29 |
| 72 | 465.3 | 447.02~483.58 |
| 75 | 526.6 | 503.10~550.10 |
平时我们并不重复抽取许多样本来一次次估计总体均数而仅是一次,至于算出的均数会类似一百个样本均数中的那一个就很难说了。如果不遇到类似上列那些均数过大或过小的样本,求出可信区间后总体均数真是在该区间内,那么便是一次成功的估计:但是极少数情况下我们也会遇到极端的样本,以至总体均数并不在我们提出的区间内。不过,我们具体所作的这次估计到底属于前种情况还是后一种,这是无法知道的,因为我们不知道 μ 是多少(若已知 μ 便不必估计它了)。然而象后种情况那样作出错估的概率终究很小,只 5% 或 1%,所以用这样的方法估计总体均数还是可行的。
三、总体率的估计
上面已经提到,计数资料可以计算相对数(率)。我们若由样本统计量 P 估计总体参数 π,同样要考虑率的抽样误差,据数理统计研究结果,样本率的分布也近似正态分布,尤其当 π 比较靠近 50% 且样本较大时。于是对样本,百分率的可信区间可利用正态分布规律估计,公式是:
95% 可信区间 P-1.96Sp<π
99% 可信区间 P-2.58Sp<π
(按正态分布,双侧尾部面积 α =0.05 时的 u 值为 1.96,α=0.01 时的 u 值为 2.58,故用这两式求可信区间时不必查表找临界 u 值,记住这两数即可。)
例 6.3 某医院收治 200 例急性菌痢患者,其中粪便细菌培养阳性者共 80 例,试估计菌痢细菌培养的总体阳性率 95% 与 99% 可信区间。
1. 求阳性率 P=80/200×100%=40%(或 0.40)
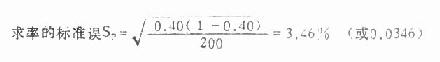
3.求可信区间
95% 可信区间 40%-1.96(3.46%)<π<40%+1.96(3.46%),即估计 π 在 33.22%~46.78% 之间
99% 可信区间 40%-2.58(3.46%)<π<40%+2.58(3.46%),即估计 π 在 31.07%~48.93% 之间
如果是小样本的百分率,求可信区间可通过查表获得,附表 4 是 n 为 10、15、20、30 时查 95% 与 99% 可信区间的一个简表。此外,统计学专著中还有更详细的表可查。
练习题
1.下列数据为某院两种疾病治愈出院者住院天数统计,试计算标准误以比较两者抽样误差的大小。
| 例数 n | 平均数 X | 标准差 S | |
| 杆菌痢疾 | 84 | 17.62 | 10.61 |
| 流行性感冒 | 90 | 6.17 | 3.49 |
2.淮南第三药厂新近研制中西药结合的复方制剂安降片,经 268 例高血压病人临床验证。显效率达 50%,试估计总体率所在的 95% 与 99% 可信区间。
3,用巯甲丙脯酸治疗心衰病人 60 名,治疗前心功Ⅲ级者 34 人,治疗后降为 15 人。求治疗前与治疗后心功Ⅲ级者所占百分比,再分别求其 95% 可信区间。
4.测定正常男、女各 25 人的血球压积(%)后,求得两组平均值与标准差为男:47.0±3.0, 女:41.2±2.8, 试求男、女血球压积(%)的 99% 可信区间。
5. 用氯霉素治疗急性菌疾 30 例,治愈 21 例,用磺胺治疗的一组中,20 例治愈 8 例,求各组治愈的 95% 可信区间。
第六章 t 检验与 u 检验
抽样研究包含参数估计与通过假设检验作统计推断这样一些重要内容。前者在第六章最后一节中已经涉及,后者如 X 2检验,我们亦已有过接触。本章将介绍两均数相比时的假设检验。
第一节 t 检验
一、样本均数与总体均数的比较
为了判断观察到的一组计量数据是否与其总体均数接近,两者的相差系同一总体中样本与总体之间的误差,相差不大;还是已超出抽样误差的一般允许范围而存在显着差别?应进行假设检验,下面通过实例介绍 t 检验的方法步骤。
例 7.1 根据大量调查得知,健康成年男子脉搏均数为 72 次 / 分,某医生在某山区随机抽查健康成年男子 25 人,其脉搏均数为 74.2 次 / 分,标准差为 6.5 次 / 分。根据这个资料能否认为某山区健康成年男子的脉搏数与一般健康成年男子的不同?
在医学领域中有一些公认的生理常数如本例提到的健康成人平均脉搏次数 72 次 / 分,一般可看作为总体均数 μ。已知在总体均数 μ 和总体标准差 σ 已知的情况下可以予测样本均数分布情况,现缺总体标准差,则需用样本标准差来估计它,那么样本均数围绕总体均数散布的情况服从 t 分布(尤其当样本含量 n 较小时,)。t 分布的基本公式即 6.5。
![]()
从式中可知,t 是样本均数与总体均数之差(以标准误为单位),t 的绝对值越大也即 X 距 μ 越远。在 t 分布中距 μ 越远的样本均数分布得越少(所占百分比小,P 值小),后面附表 3 右上角的示意图中展示了这种关系,如欲知各自由度下 t 值与其相应的 P 值可查附表 3。
下面回答本例提出的问题而进行假设检验。按一般步骤:
(1)提出检验假设 H 与备择假设 H 1。本例 H 为某山区成年男子的脉搏均数与一般成年男子的相等,μ=μ=72 次 / 分;H1为两者不相等 μ≠μ,即 μ 大于或小于 μ(这是双侧检验,如果事先已肯定山区人的脉搏不可能低于一般人,只检验它是否高于一般人,则应用单侧检验,H1必为 μ >μ)。
(2)定显著性水准 α,并查出临界 t 值。α 是:若检验假设为真但被错误地拒绝的概率。现令 α =0.05,本例自由度 ν =n-1=25-1=24、查附表 3 得 t 0.05,24=2.064。若从观察资料中求出的∣t∣值小于此数,我们就接受 H;若等于或大于此值则在 α =0.05 水准处拒绝 H 而接受 H 1。
(3)求样本均数 X、标准差 S 及标准误 S χ并进而算出检验统计量 t。现已知 X =74.2 次 / 分,S=6.5 次 / 分,只要求出 S χ及 t 值即可。
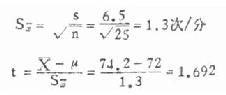
(4)下结论:因∣t∣t0.05,24=2.064,所以检验假设 H 得以接受,从而认为就本资料看,尚不能得出山区健康成年人的脉搏数不同于一般人而具有显著差别的结论。
二、成对资料样本均数的比较
上面介绍了已知总体均数时的显着性检验方法,但有时我们并不知道总体均数,且医学数据资料中更为常见的是成对资料,若一批某病病人治疗前有某项测定记录,治疗后再次测定以观察疗效,这样,观察 n 例就有 n 对数据,这即是成对资料(也可对动物做成病理模型进行治疗实验以收集类似的成对资料);如果有两种处理要比较,将每一份标本分成两份各接受一种处理,这样观察到的一批数据也是成对资料,医学科研中有时无法对同一批对象进行前后或对应观察,而只得将病人(或实验动物)配成对子,尽量使同对中的两者在性别、年龄或其它可能会影响处理效果的各种条件方面极为相似,然后分别给以一种不同的处理后观察反应,这样获得的许多对不可拆散的数据同样是成对资料。由于成对资料可控制个体差异使之较小,故检验效率是较高的。
关于成对资料,每对数据始终相联这是它的特点,我们可以先初步观察每对数据的差别情况,进一步算出平均相差作为样本均数,再与假设的总体均数比较看相差是否显著,下面举实例说明检验过程。
表 7.1 豚鼠注入上腺素前后每分钟灌流滴数
| 豚鼠号 | 每分钟灌流滴数 | ||
| 用药前 | 用药后 | 增加数 d | |
| 1 | 30 | 46 | 16 |
| 2 | 38 | 50 | 12 |
| 3 | 48 | 52 | 4 |
| 4 | 48 | 52 | 4 |
| 5 | 60 | 58 | -2 |
| 6 | 46 | 64 | 18 |
| 7 | 26 | 56 | 30 |
| 8 | 58 | 54 | -4 |
| 9 | 46 | 54 | 8 |
| 10 | 48 | 58 | 10 |
| 11 | 44 | 36 | -8 |
| 12 | 46 | 54 | 8 |
| 总 计 | — | — | 96 |
例 7.2 为了验证肾上腺素有无降低呼吸道阻力的作用,以豚鼠 12 只,进行支气管灌流实验,在注入定量肾上腺素前后,测定每分钟灌流滴数,结果见表 7.1,问用药后灌流速度有无显著增加?
(1)假设用药前后灌流滴数相同,则相差的总体均数 μ 为 0;即 H:μ=μ;H1:μ≠μ。
(2)令显著性水准 α =0.05,由本例 ν =12-1=11 查得临界值 t 0.05,11=2.201。
(3)求样本统计量平均相差数 d、差数的标准差 S d、标准误 Sd 及检验统计量 t 值。

(4)下结论。今∣t∣t0.05,11,p <0.05,故认为检验假设 μ = μ 难以接受,在 α =0.05 水准外拒绝 H O而接受 H 1,相差显著,注入肾上腺素后每分钟灌流滴数比注射前要多。
例 7.3 从以往资料发现,慢性支气管炎病人血中胆碱酯酶活性常常偏高。某校药理教研室将同性别同年龄的病人与健康人配成 8 对,测量该值加以比较,资料如下。问可否通过这一资料得出较为明确的结论?
表 7.2 慢性气管炎病人与健康人血液胆碱酯酶活性测定(μM/ml)
| 对子序号 | 病人组,X1 | 健康人组,X2 | 差数 D =X1-X2 |
| 1 | 3.28 | 2.36 | 0.92 |
| 2 | 2.60 | 2.40 | 0.20 |
| 3 | 3.32 | 2.40 | 0.92 |
| 4 | 2.72 | 2.52 | 0.20 |
| 5 | 2.38 | 3.04 | -0.66 |
| 6 | 3.64 | 2.64 | 1.00 |
| 7 | 2.98 | 2.56 | 0.42 |
| 8 | 4.40 | 2.40 | 2.00 |
(1)检验假设 H:μ=μ;H1:μ>μ
(2)令 α =0.05,得 t 0.05,7=1.895(单侧)
(3)用差数求统计量
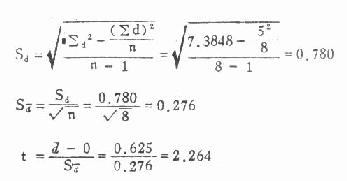
(4)结论∣t∣=2.264>t0.05,7=1.895,P<0.05, 在 α =0.05 水准处拒绝 H,接受备择假设,认为慢性气管炎病人血中胆碱酯酶高于正常人。
上例用了单侧检验是因为事先并不认为该类病人血中胆碱酯含量会出现低于健康人的情况。
三、两组资料样本均数的比较
在日常工作中,我们经常要比较某两组计量资料的均数间有无显着差别,如研究不同疗法的降压效果或两种不同制剂对杀灭鼠体内钩虫的效果(条数)等。这时假若事先难以找到年龄、性别等条件完全一样的人(或动物)作配对比较,那么不能求每对的差数只能先算出各组的均数,然后进行比较。两组例数可以相等也可稍有出入。检验的方法同样是先假定两组相应的总体均数相等,看两组均数实际相差与此假设是否靠近,近则把相差看成抽样误差表现,远到一定界限则认为由抽样误差造成这样大的相差的可能性实在太小,拒绝假设而接受 H 1, 作出两总体不相等的结论。
例 7.4 为观察中成药青黛明矾片对急性黄疸肝炎的退黄效果,以单用输液保肝的病人作为对照进行了观察,两组患者均为成人,黄疸指数在 30-50 之间,各人退黄天数如下,试比较用药组(1 组)与对照组(2 组)退黄天数有无显著差别。
表 7.3 急性黄疸性肝炎病人的退黄天数
| 中药组,X1 | 5 | 10 | 14 | 21 | 17 | ∑X1=67 | |
| 对照组,X2 | 18 | 21 | 30 | 23 | 22 | 22 | ∑X2=136 |
(1)检验假设 设该药对缩短退黄天数无效,两组的总体均数相等,即 H =μ1=μ2;H1:μ1≠μ2。
(2)求自由度 ν
ν=n1+n2-2
=5+6-2=9 (7.1)
定 α =0.05,ν= 9 时的 t 值为 t 0.05,9=2.262
(3)计算各组均数,合并方差 S 2c及两均数相差的标准误 S χ1-χ2,然后求 t 值。
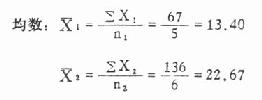
合并方差: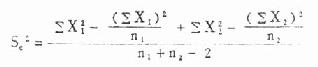 (7.2)
(7.2)
代入得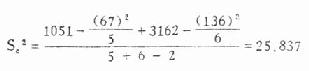
两均数相差的标准误:
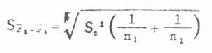 (7.3)
(7.3)
代入得
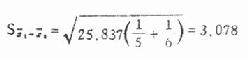
求 t:
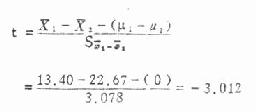 (7.4)
(7.4)
(4)下结论 因│t┃>t0.05,9,P<0.02,所以我们在 α =0.05 水准处拒绝 H 而接受 H 1,两者平均退黄天数和有显著差别,服青黛明矾片药的病人退黄天数较短。如果检验假设属实,这样的结论也还可能下错,但概率在 2% 以下。
上例为两组资料均数间的比较,与前面成对资料的 t 检验有些区别。前者每对中两数据不能分离,后者任一组中的各数据可以在组内前后互换位置;前者只有一个样本平均差数 d 对应于一个假设的总体平均差数 μ,后者,认为 X 1为第一个总体的随机样本均数,X2则来自 μ 2,所以后者要计算两组合并的方差 S 2c(方差是标准差的平方)。再者,与前者相比标准误、自由度的计算方法也不相同。
例 7.5 某人测定半岁至 1 岁小儿、7 至 8 岁儿童各 9 人的免疫球蛋白 IgG(国际单位 /ml),算得平均数与标准差前者(第 1 组)为 55.1± 11.5, 后者(第 2 组)为 95.5 ±17.8,试检验这两种不同年龄的人免疫球蛋白 IgG 有无显著差别。
(1)检验假设 H:μ1=μ2;H1:μ1≠μ2。
(2)令 α =0.01, 查自由度 ν =9+9-2=16 时的临界值,得 t 0.01,16=2.921
(3)求统计量 已知 X 1=55.1,X2=95.5, 至于求 t 值时作为分母的标准误,在暂缺原始数据时由已知的两个标准差先推算出合并方差 S c2进而求出 S χ1–χ2即可,方法如下;
①一般方法;根据标准差算式
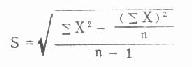
则
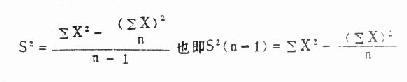
于是
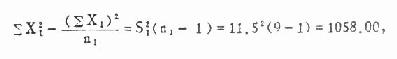
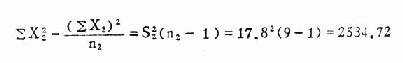
由式(7.2)
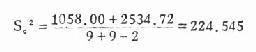
由式(7.3)
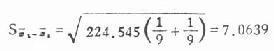
②在两组例数相等时也可直接用 S 1、S2代入下式求 S χ1–χ2,结果一样。
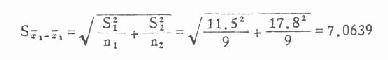
现已有了均数及标准误可由 X 1、X2、Sχ1–χ2求出 t 值。
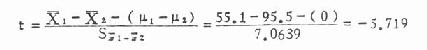
(4)结论 │t│>=5.719>t0.01,16=2.921,P<0.001,在 α =0.01 水准处拒绝 H,接受 H 1,两年龄组的人免疫球蛋白 IgG 的均数相差显著,7- 8 岁组的高于小几组。
关于检验水准 α 定在 0.05 还是 0.01 或其它处,要看检验者事先对结论的可靠性要求之高低而定。本例定 α =0.01,要求是较高的,最后查出 P 值小于 0.001 就更说明 X 1-X2=-40.4 随机来自 μ 1-μ2= 0 的假设总体的可能性是很小的。
第二节 u 检验
u 检验(亦称 T 检验),它根据正态分布规律作假设检验(显着性检验)。当样本含量增大时,样本均数的分布趋向正态,这可看图 6.1,t 分布曲线以 ν = 9 的一条比 ν = 3 的更近似正态分布,再看附表 3,表最下一行 ν 为∞时的 t 分布即是正态分布。故 u 检验用于大样本。
在仅有一条的标准正态曲线上,以 u =1.96 与 -1.96 为界,从此处向外的尾部面积共占 5%,即∣u∣≥1.96 相应的 P 值为 0.05,又∣u∣≥2.58 相应的 P 为 0.01。通常我们取 α =0.05 或 α =0.011 作为显着性检验水准,故临界值 u 0.05=1.963 及 u 0.01=2.58 最好能记住而省得查表。
一、两均数的比较
例 7.6 某工业区卫生防疫站为掌握学龄儿童免疫球蛋白水平,对一批无结核及肾炎病史,一月内无急性感染,又未进行预防接种的学生作了血清 IgM(mg/dl)测定,其中 12 岁男孩 73 人的 X±S 为 125±54,12 岁女孩 68 人的为 153±75,试比较 12 岁男、女孩的 IgM 水平有无显着差别。
这里令男生为第 1 组,女生为第 2 组。
(1)检验假设 H:μ1=μ2;H1:μ1≠μ2。
(2)定 α =0.05 则对应于 P 为 0.05 时的 u 0.05值为 1.96。
(3)求两均数的相差数 X 1-X2、两均数相差的标准误 S χ1–χ2及 u 值。此外,计算 S χ1–χ2的公式为
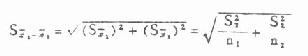 (7.5)
(7.5)
将有关数字代入得
X1-X2=125-153=-28
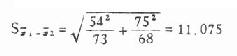
然后求 u
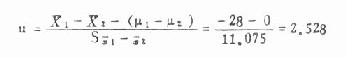
(4)结论 因│u┃>u0.05=1.96,P<0.05。在 α =0.05 水准处拒绝 H 而接受 H 1,即 μ 1≠μ2,故认为 12 岁女孩的血清免疫球蛋白 IgM 高于同龄男孩。
二、两个率的比较
关于计数资料,求出特征数百分率后,率与率的比较一般采用第三章介绍的 X 2检验法,在大样本时,根据样本率分布呈正态分布的特点,也可用 u 检验。
例 7.7 某地曾流行一种原因不明的皮炎,有关部门进行调查时,以宅旁有桑毛虫寄生树的人群为观察组(第 1 组),以宅旁无该树者为对照组(第 2 组),两组患病率如下,经显着性检验可得什么结论?
表 7.4 两组皮炎患病率
| 组 别 | 观察例数 | 患者 | 患病率(%) |
| 观察组 | 144 | 105 | 72.92 |
| 对照组 | 139 | 66 | 47.48 |
| 合 计 | 283 | 171 | 60.42 |
(1)检验假设 HO:两组相应的总体率相等即 π 1=π2,H1:π1≠π2。
(2)显著性水准 为使结论更加可靠,定 α =0.01,则 1% 界 u 0.01=2.58。
(3)求两样百分率的相差、两百分率相差的标准误 Sp1—p2 及 u 值。
![]()
式内 π 为两组合计百分率,此例为 0.6042,见表 7.4 合计栏。
![]() (7.6)
(7.6)
将有关数字代入得

(4)结论 │u│=4.379>u0.01=2.58,P<0.01,也即在 α =0.01 水准处拒绝 H,接受 H 1,即 μ 1≠μ2,宅旁有桑毛虫寄生树的人群皮炎患病率较高。
此外,两百率相差的标准误 Sp1-p2还有近似计算公式如下;
![]() (7.7)
(7.7)
式中 S 2P1、S5P2分别为第 1、2 两组百分比的标准误的平方,标准误计算公式即式(6.4)
![]()
用上例数据代入可算得

这里,标准误与 u 值尽管和前面算得的稍有出入,但还是│u│>u0.01=2.58,P<0.01,结论相同。
第三节 正态性检验与两方差的齐性检验
检验两个样本均数相差的显着性时,我们先有假定:第一个样本系从均数为 μ 1、方差为 σ 12的正态总体中随机取出,第二个样本取自另一个类似的总体,相应的总体参数为 μ 2与 σ 22,两个总体的方差应相等即 σ 12=σ22,然后才可用上述方法进行显着性检验,如果资料呈显着偏态,或两组方差相差悬殊,就要考虑用第十章非参数统计方法处理,或者通过变量代换,使上述条件得到满足。那么,怎样知道手头的样本资料是否服从正态分布及两组方差是否相差显著呢?要对手头资料作正态检验及方差齐性检验。下面分别用实例介绍常用的正态性检验和两方差齐性检验的方法。
一、正态性检验
有些统计方法只适用于正态分布或近似正态分布资料,如用均数和标准差描述资料的集中或离散情况,用正态分布法确定正常值范围及用 t 检验两均数间相差是否显着等,因此在用这些方法前,需考虑进行正态性检验。
正态分布的特征是对称和正态峰。分布对称时众数和均数密合,若均数 - 众数 >0,称正偏态。因为有少数变量值很大,使曲线右侧尾部拖得很长,故又称右偏态;若均数 - 众数 <0 称负偏态。因为有少数变量值很小,使曲线左侧尾部拖得很长,故又称左偏态,见图 7.1(a)。
正态曲线的峰度叫正态峰,见图 7.1(b)中的虚线,离均数近的或很远的变量值都较正态峰的多的称尖峭峰,离均数近或很远变量值都较正态峰的少的称平阔峰。
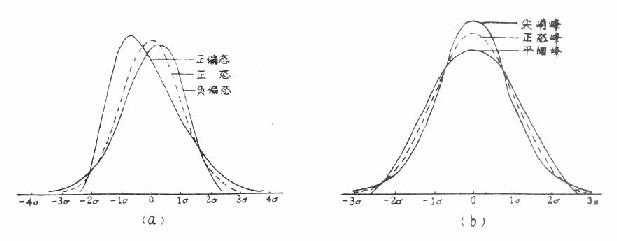
图 7.1 频数分布的偏度和峰度
正态性检验的方法有两类。一类对偏度、峰度只用一个指标综合检验,另一类是对两者各用一个指标检验,前者有 W 法、D 法、正态概率纸法等,后者有动差法亦称矩法。现仅将 W 法与动差法分述于下;
1.W 法 此法宜用于小样本资料的正态性检验,尤其是 n≤50 时,检验步骤如下;
(1)将 n 个变量值 X i从小至大排队编秩。
X1<x2<……<xn<p< p=””></xn<p<></x
见表 7.5 第(1)栏,表中第(2)、第(3)栏是变量值,第(2)栏由上而下从小至大排列,第(3)栏由下而上从小至大排列。第(4)栏是第(3)栏与第(2)栏之差。
(2)由附表 5 按 n 查出 a in系数列入表 7.5 第(5)栏,由于当 n 为奇数时,对应于中位数秩次的 a in为 0,所以中位数只列出,不参加计算。第(6)栏是第(5)栏与第(4)栏的乘积。
(3)按式(7.8)计算 W 值
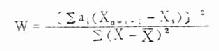 (7.8)
(7.8)
式中分子的∑,当 n 是偶数时,为![]() 的缩写,当 n 是奇数时为
的缩写,当 n 是奇数时为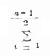 的缩写,表 7.5
的缩写,表 7.5
第(6)栏的合计平方后即为分子。分母按原始资料计算。
(4)查附表 6 得 P 值,作出推断结论,按 n 查得 W(n,α),α 是检验前指定的检验水准,若 W >W(n,α)则在 α 水准上按受 H,资料来自正态分布总体,或服从正态分布;若 W≤W(n,α),则在 α 水准上拒绝 H,接受 H 1,资料非正态。
例 7.8 测得 20 例 40—49 岁健康人右侧腓总神经的传导速度(m/sec)如表 7.5 第(2)、第(3)栏,试检验此资料是否服从正态分布。
H:总体服从正态分布
H1:总体为非正态分布
α=0.05
计算表 7.5 各栏。
表 7.5 W 法正态性检验计算表
| 秩号 | 传导速度(m/sec) | ||||
| i(1) | Xi(2) | Xa-i+1(3) | Xa-i+1-Xi(4)=(3)-(2) | ain(5) | ain(Xa-i+1-Xi)(6)=(5)(4) |
| 1 | 40.7 | 56.7 | 16.0 | 0.4734 | 7.5744 |
| 2 | 40.9 | 56.0 | 15.1 | 0.3211 | 4.8486 |
| 3 | 46.0 | 55.0 | 9.0 | 0.2565 | 2.3085 |
| 4 | 47.6 | 54.9 | 7.3 | 0.2085 | 1.5221 |
| 5 | 47.7 | 53.5 | 5.8 | 0.1686 | 0.9779 |
| 6 | 48.3 | 52.9 | 4.6 | 0.1334 | 0.6136 |
| 7 | 49.1 | 51.8 | 2.7 | 0.1013 | 0.2735 |
| 8 | 50.0 | 50.9 | 0.9 | 0.0711 | 0.0640 |
| 9 | 50.1 | 50.9 | 0.8 | 0.0422 | 0.0338 |
| 10 | 50.2 | 50.8 | 0.6 | 0.0140 | 0.0084 |
| 18.2240∑ain(Xa-i+1-Xi) | |||||
∑Xi=1004 ∑Xi2=50756.16 ∑(X-x)2=355.36
代入式(7.8)
W=(18.2240)2/355.36=0.9347
查附表 6,n=20,α=0.05,W(20,0.05)=0.905
W>W(20,0.05)P>0.1,在 α =0.05 水准上接受 H,该资料服从正态分布。
2.动差法 又称矩法。既能用于小样本资料,亦可用于大样本资料的正态性检验。本法运用数学上三级动差和四组动差分别组成偏度系数与峰度系数,然后检验资料中否服从正态分布。当频数分布为正态时,偏度系数与峰度系数分别等于 0,但从正态分布总体中抽出的随机样本,由于存在抽样误差,其样本偏度系数 g 1与样本峰度系数 g 2不一定为 0,为此,需检验 g 1、g2与 0 的相差是否有显著性。其检验假设为①偏度系数等于 O,即频数分布对称;②峰度系数等于 0,即为正态峰。
偏度系数 g 1、峰度系数 g 2的公式见式(7.9)与(7.11)。当用频数表资料计算时可用式(7.10)与式(7.12),式中 n 为例数,f 为频数。
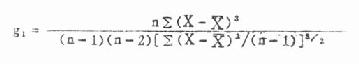
![]() (7.10)
(7.10)
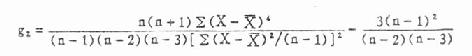 (7.11)
(7.11)
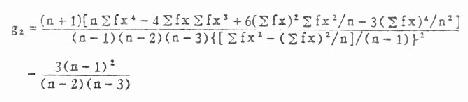 (7.12)
(7.12)
g1、g2的抽样误差分别为 S g1与 S g2,见式(7.13)与式(7.14)
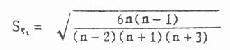 (7.13)
(7.13)
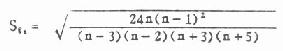 (7.14)
(7.14)
假设检验用 u 检验,其公式为
u1=g1/Sg1(7.15)
u2=g2/Sg2(7.16)
u 的显著性界限为
∣u∣<1.96P>0.05 在 α =0.05 的水准上接受 H。
1.96≤∣u∣<2.580.05≥P>0.01 在 α =0.05 的水准上拒绝 H。
∣u∣≥2.58P≤0.01 在 α =0.01 的水准上拒绝 H。
例 7.9 用动差法检验例 7.8 的资料是否服从正态分布。
1.H:频数分布对称,H1:频数分布不对称。
2.H:频数分布为正态峰,H1:频数分布不是正态峰。
α=0.05
∑(X-x)2=355.36,∑(X-x)3=-1032.45
∑(X-x)4=20150.4316 n=20

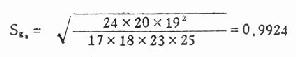
u2=0.6221/0.9924=0.627 P>0.20
在 α =0.05 的水准上接受 H,频数分布对称(P>0.05),并为正态峰(P>0.20)。因此可认为该资料服从正态分布。
二、两方差的齐性检验
方差齐性检验的方法是以两方差中较大的方差为分子,较小的方差为分母求一比值(称为 F 值),然后将求得的 F 值与临界值比较,看相差是否显着,现举一例说明。
例 7.10 某单位测定了蓄电池厂工人 32 号,得尿氨基乙酰丙酸(mg/l)的平均含量为 7.06,方差为 42.3072,又测定了化工厂工人 6 名,得平均含量为 3.48,方差为 0.9047,试比较两方差的相差是否有显着意义?
检验假设 H:σ12=σ22,H1:σ12≠σ22α=0.05
定方差较大的一组为第 1 组,较小者为第 2 组,求出 F 值,公式为
F=S12/S22,S1>S2(公式 7.17)
本例 F =42.3072/0.9047=46.76
现将 F 值与附表 7 中的 F .05(ν1,ν2)比较。该表上端数值是较大均方(即方差)的自由度,用 v1 表示,左侧的数值是较小均方的自由度,用 ν 2表示。本例 ν 1=n1-1=32-1=31(表内 ν 1纵行没有 31,可查邻近的数值 30),ν2=n2-1=6-1=5, 查得 F .05(30,5)=6.23, 本例 F =46.76>F.05(30,5),P<0.05, 故在 α =0.05 水准处拒绝 H,接受 H 1。两方差的差别显著。
练习题
1.用某药治疗 10 名高血压病人,对每一病人治疗前、后的舒张压(mmHg)进行了测量,结果如下,问该药有无降压作用?
10 名高血压病人治疗前后的舒张压(mmHg)
| 病例编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 8 | 10 |
| 治疗前 | 117 | 127 | 141 | 107 | 110 | 114 | 115 | 138 | 127 | 122 |
| 治疗后 | 123 | 108 | 120 | 107 | 100 | 98 | 102 | 152 | 104 | 107 |
2.某医院病理科研究人体两肾的重量,下面是 20 例男性尸解时左、右两肾的称重记录,问左、右两肾重量有无显著差别?
| 左肾(克) | 170 | 155 | 140 | 115 | 235 | 125 | 130 | 145 | 105 | 145 | 155 | 110 | 140 |
| 145 | 120 | 130 | 105 | 95 | 100 | 105 | |||||||
| 右肾(克) | 150 | 145 | 105 | 100 | 222 | 115 | 120 | 105 | 125 | 135 | 150 | 125 | 150 |
| 140 | 90 | 120 | 100 | 100 | 90 | 125 |
3.设有 13 例健康人,11 例克山病人的血磷测定值(mg%)如下表所示,问克山病人的血磷是否高于健康者?
| 健康者 | 1.67 | 1.98 | 1.98 | 2.33 | 2.34 | 2.50 | 3.60 | 3.73 | 4.14 | 4.17 | 4.57 | 4.82 | 5.78 |
| 患 者 | 2.60 | 3.24 | 3.73 | 3.73 | 4.32 | 4.73 | 5.18 | 5.58 | 5.78 | 6.40 | 6.53 |
4.某生化实验室测定了几组人的血清甘油三酯含量(mg%)见下表,试分别比较工人与干部,男与女的该项血酯水平。
正常成人按不同职业、性别分类的血清甘油三酯含量
| 人 数 | 平均数 | 标准差 | |
| 工 人 | 112 | 106.49 | 29.09 |
| 干 部 | 106 | 95.93 | 26.63 |
| 男 | 116 | 103.91 | 27.96 |
| 女 | 102 | 97.93 | 28.71 |
5 . 肺结核及结核性胸膜炎各 5 例的血沉(一小时)值如下表,问两者的差别显著否?
| 肺 结 核 | 12 | 20 | 30 | 8 | 15 |
| 结核性胸膜炎 | 80 | 50 | 30 | 30 | 70 |
(请注意,两组病人的个体差异差别大否即方差齐否?试用一般的 t 检验与将各原始数据化成常用对数(定值部可取三位小数)后作 t 检验。将结果比较一下,是否一致?此资料应采取哪一种方法处理为妥?
6.经大量调查认为,正常人末梢血中性粒细胞碱性磷酸酶活性阳性率平均为 41%,某人报告,观察 42 例健康人的阳性率为 54.8%,问这一结果是否较通常的高?
7.某人用灭虫宁治疗蛔虫症 126 例,完全净除率为 15.87%(20 例),治疗钩虫症 225 例,完全净除率 19.56%(44 例),问两者效果有差别否?
8.试分别检验第 3 题健康人与克山病人的血磷值是否服从正态分布。
第七章 方差分析
第一节 方差分析的意义
在第七章我们已介绍了两个样本均数相比较的显着性检验方法。如果相互比较的组超过两个,为同时解决几个均数的比较问题,通常使用方差分析法。
方差即标准差 σ 或 S 的平方,又称均方,它由离均差平方和被自由度相除而得。方差分析时我们将总离均差平方和即总变异分析为几个组成部分,其自由度也分解为相应的几部分,故方差分析又称变异数分析。它是处理实验研究资料时重要的分析方法之一,内容很多,本章仅介绍两个以上样本均数差别的显着性检验。
检验前对资料应有如下要求:被比较的各组应分别随机来自各自的正态总体,各总体相互独立并具有相同的方差即 σ 12=σ22=σ32……σk2。检验假设为,H:μ1=μ2=μ3……=μk,H1:各总体均数不全相等。下面通过实例先介绍完全随机设计资料的方差分析。
第二节 安全随机设计资料的方差分析
一、检验的一般步骤
1.资料 这里所要的是类似第七章第一节三、中所述的成组资料,不过现在不是两组而是多组,如下例。
例 8.1 分泌型免疫球蛋白 A(SIgA)是胃肠道分泌液、泪液等外分泌液中的主要免疫球蛋白类,某院研制了“125I-SIgA 放射免疫测定药盒”,为人体 SIgA 的检验提供了一种简便方法。为比较不同批号药盒检验结果是否一致,该院曾将三批号各四个药盒一一测定了某一标本得结果如下,试作方差分析。
表 8.1 三个批号药盒的 SIgA 放射免疫测定值
| 批号 | SIgA 含量(μg/ml), X | ∑X | n | X | ∑X2 | ∑X2-(∑X)2/n | |||
| 1 | 1.92 | 1.80 | 2.08 | 2.00 | 7.80 | 4 | 1.95 | 15.2528 | 0.0428 |
| 2 | 2.21 | 2.25 | 2.12 | 2.57 | 9.15 | 4 | 2.29 | 21.0459 | 0.1153 |
| 3 | 3.27 | 2.75 | 2.90 | 3.10 | 12.02 | 4 | 3.01 | 36.2754 | 0.1553 |
| 合计 | 28.97 | 12 | 2.414 | 72.5741 | 0.3134 | ||||
2. 分析 从表 8.1 的测定结果可以看出这里有三种变异:
(1)从同一批号药盒的四次测定结果看,不尽相同,这是组内变异。显然它不是由于批号不同的影响,而只是由于误差(如批内各药盒的差异性和测量误差等)造成的。
(2)从各批测定值的均数来看,是不相同的,这是组间变异,表明各批药盒性能质量也许对测得的结果有一定影响,也包括误差的作用。
(3)12 次测定的 SIgA 含量都不尽相同,有高有低,它们既可能受药盒来自不同批号的影响,也包括组内变异,因此称为总变异。
那么这里各批药盒测 SIgA 均值间的差别,只不过是抽样误差的反映呢?还是药盒制作质量不稳定,批间存在显著差别?为了得出正确的结论,可进行方差分析。方差分析的基本甲思想是:①从总变异中分出组间变异和组内变异,并用数量表示变异的程度;②将组间变异和组内变异进行比较,如两者相差不大,说明受批号不同的影响不大;如果两者相差较大,组间变异比组内变异大得多,说明批号不同的影响不容忽视。下面我们根据表 8.1 资料来计算这三种变异。
(1)总离均差平方和:即 12 个观察值各与总均数相差的平方之和,公式为
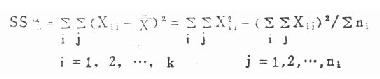 (8.1)
(8.1)
式中 SS 总即总离均差平方和,Xij 表示第 i 组的第 j 个观察值,X 为全部观察值的平均数,k 是组数。
本例 SS总=72.5741-28.972/12=2.6357
(2)组间离均差平方和:即取各组均数代替该组各观察值后,它们分别与总均数相差的平方之和,公式为
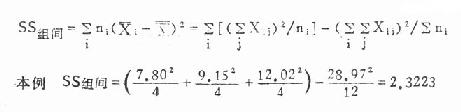 (8.2)
(8.2)
(3)组内离均差平方和:只要加总各组本身的离均差平方和即得,公式为
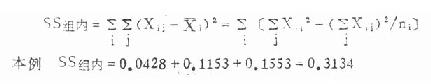 (8.3)
(8.3)
由本例计算结果可以看出,SS组间 +SS 组内 =SS 总,如 2.3223+0.3134=2.6357。因此,算出 SS总 以后再计算 SS组间 、SS 组内 两者中之一个,其余一个便可通过减法求得。
将以上求得的几种变异各除以自由度后得均方。自由度的计算公式分别为
总变异 N-1(N 为各组例数之和)(8.4)
组间变异 K-1(8.5)
组内变异 N-K(8.6)
组间均方与组内均方之比为 F 值,
F=组间均方 / 组内均方(8.7)
本例
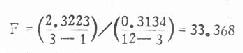
将以上数据列入下面的方差分析表可使人一目了然。
表 8.2 方差分析表
| 变异来源 | 离均差平方和 | 自由度 | 均 方 | F |
| 总 变 异 | 2.6357 | 11 | ||
| 组间变异 | 2.3223 | 2 | 1.1612 | 33.368 |
| 组内变异 | 0.3134 | 9 | 0.0348 |
如果求得的 F 值小于 1 或略大于 1,也即组间变异与组内变异差不多,则关于不同批药盒所致影响就不值得注意,反之,若各批均数间差别甚大,组间变异比组内变异大得多,说明不能只把它看成为误差的表面,很可能不同批药盒的测定值具有差别。现 F 值远大于 1,若等于或大于某 α 水准下的临界 F 值,便将拒绝检验假设 H 而接受备择假设 H 1。
本例定 α =0.05, 查附表 8F 值表,F0.05(2,9)=4.26。括弧内 2 为求 F 值时分子(也即较大均方)的自由度,9 为分母的自由度,今 F =33.368,远大于此临界值 4.26, 故 P <0.05,说明不同批药盒的影响不容忽视,各批药盒测定的 SIgA 值相差显著。
二、多个均数间的两两比较
经方差分析(即 F 检验),若各组均数之间差别不显着,则到此为止,不必作进一步统计学处理了。当 F 检验结果为相差显着时,这只是对各组均数的整体而言,至于哪些均数间的差别显着,哪些不显着,还要作如下进一步分析。
本例检验结果为相差显着,这里我们先用较为简单而实用的最小显着差数法来比较三组中每两组均数间的差别是否显着,然后介绍 q 值法。
1.最小显着差数法
(1)计算最小显着性差数 D α,ν
Dα,ν=t,![]() (8.8)
(8.8)
式中 t,由附表 3 查得,查时自由度 ν 用方差分析表中组内变异的自由度,本例为 9;α 即显著性水准,常用 0.05 或 0.01,本例查得两个临界 t 值即 t 0.05,9=2.262,t0.01,9=3.250。标准误![]() 的计算公式是
的计算公式是
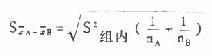 (8.9)
(8.9)
S2组内 也即表 8.2 中的组内均方(也可叫误差均方)0.0348。nA、nB为所比较的两组的例数,本例各组例数都为 4。现将数据代入式(8.9)、(8.8)求得
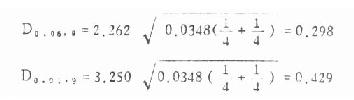
(2)用上述的最小显著性差数与每两组均数的相差数比,若后者大于前者(临界值),便相差显著,若小于前者,为相差不显著。现将两均数间的比较结果列于下表。
表 8.3 均数间两两比较
| A 与 B(批号) | ∣XA-XB∣ | 界 值 | P 值 | |
| D0.05 | D0.01 | |||
| 1 与 2 | 0.34 | 0.298 | 0.429 | <0.05 |
| 1 与 3 | 1.06 | 0.298 | 0.429 | <0.01 |
| 2 与 3 | 0.72 | 0.298 | 0.429 | <0.01 |
注:表中 X A-XB两侧的直杠是绝对值符号。
3.统计结论:各批间均在 α =0.05 水准处相差显著,又第 3 批与第 1、2 两批比,P<0.01,说明各批药盒对 SIgA 的检测效果不一致,批号 3 远高于批号 2 与 1。
上面介绍的多个均数间两两比较的方法虽较简便,精确性有时不足,尤其当比较的均数不是在三个而是更多,或各样本含量不相等时应用也较麻烦。下面介绍查临界 q 值而不查 t 值的另一比较方法。
2.q 值法
(1)将表 8.1 中三个均数自大至小排列得:
| 第 3 批 | 第 2 批 | 第 1 批 | |
| SIgA 平均值,X(μg/ml) | 3.01 | 2.29 | 1.95 |
| 秩次 | 1 | 2 | 3 |
| 样本含量,n | 4 | 4 | 4 |
(2)用组内均方与平均每组例数 n 求出标准误,然后与由附表 9 中查到的临界 q 值相乘,即可列出比较表加以比较。下面是求平均例数的公式。
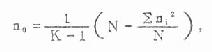 (i=1,2,…,k) (8.10)
(i=1,2,…,k) (8.10)
此例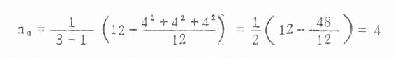
本例各组样本大小相等,均为 4,本无须用上式计算,但若各组大小不等时就得用上式求平均例数。
标准误公式为
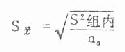 (8.11)
(8.11)
此例![]()
表 8.4 均数间两两比较
| A 与 B (秩次) | 组数 α | ∣XA-XB∣ | Q0.05(a,ν)Sχ | ν 见组内变异一行 P 值 |
| 3 与 2 | 2 | 0.34 | 0.299 | <0.05 |
| 3 与 1 | 3 | 1.06 | 0.369 | <0.05 |
| 2 与 1 | 2 | 0.72 | 0.299 | <0.05 |
现将上表栏目自左至右一一说明如下:
表内左侧,均数大小秩次 3 与 2 比,即相邻两组相比,故组数 a 等于 2。同样,第三行的 2 与 1 比,因 2 与 1 相邻,a 也是 2,3 与 1 比则由 3 到 1 组数有 3,a 等于 3。关于查附表 9 中的 q 值,一方面根据该表上端横行 a 的数字,另方面根据表左侧直行的 ν,也即方差分析表中组内(或误差)项的自由度(本例为 9)来查。表内 q 值有上、下两行数,若定 α 为 0.05,查上行,α 为 0.01 则查下行。
就本例言,用两种方法作均数间两两比较,其结论完全一致。
例 8.2 下表为用动物研究白血病时测得的鼠脾 DNA(脱氧核糖核酸)含量,现作方差分析,比较四个不同病情组的均数相差是否显著。
表 8.5 鼠脾 DNA 含量测定值(mg)
| 正常组 | 患自发性白血病组 | 患移植白血病 | 总 计 | ||
| 甲组 | 乙组 | ||||
| 12.3 | 10.8 | 9.3 | 9.5 | ||
| 13.2 | 11.6 | 10.3 | 10.3 | ||
| 13.7 | 12.3 | 11.1 | 10.5 | ||
| 15.2 | 12.7 | 11.7 | 10.5 | ||
| 15.4 | 13.5 | 11.7 | 10.5 | ||
| 15.8 | 13.5 | 12.0 | 10.9 | ||
| 16.9 | 14.8 | 12.3 | 11.0 | ||
| 17.3 | 12.4 | 11.5 | |||
| 13.6 | |||||
| ∑Xijj | 119.8 | 89.2 | 104.4 | 84.7 | 398.1 |
| ni | 8 | 7 | 9 | 8 | 32 |
| Xi | 14.98 | 12.74 | 11.60 | 10.59 | 12.44 |
| ∑X2ijj | 1815.96 | 1147.32 | 1223.58 | 899.15 | 5086.01 |
| SSi | 21.96 | 10.66 | 12.54 | 2.39 | 47.55 |
1.作检验假设 H:μ1=μ2=μ3=μ4,H1:各总体均数不都相等。α=0.01。
2.用表 8.5 下部数字计算离均差平方和:简法是先求校正数 C =(∑X)2/N=398.12/32,再求
SS总:5086.01-(398.1)2/32=133.40
SS组间:(119.8)2/8+(89.2)2/7+(104.4)2/9+(84.7)2/8-(398.1)2/32=85.85
SS组内:133.40-85.85=47.55
3.列出方差分析表
表 8.6 方差分析表
| 变异来源 | 自由度 | 离均差平方和 | 均方 | F |
| 总 计 | 31 | 133.40 | ||
| 组 间 | 3 | 85.85 | 28.62 | 16.48 |
| 组 内 | 28 | 47.55 | 1.70 |
4.查 F 值表,下结论。看附表 8(3),根据求 F 值时组间均方较大,于是用其自由度 3 及组内均方的自由度 28 查得 F 0.01(3,28)=4.57,今 F =16.84>F0.01(3,28)=4.57,故在 α =0.01 水准处相差显著,P<0.01。四组鼠脾的 DNA 含量不等。(注:F 小于 1 时无须查表)。
5.为详细分析每两组间的相差情况,作两两比较如下。(因各组例数不等又组数较多,故用 Q 值法比较)。
(1)将四组均数按大小排列:
| 正常组 | 患白发性 白血病组 | 患移植白血病 | ||
| 甲组 | 乙组 | |||
| DNA 平均含量(mg) | 14.98 | 12.74 | 11.60 | 10.59 |
| 秩次 | 1 | 2 | 3 | 4 |
| 样本含量,n | 8 | 7 | 9 | 8 |
(2)求平均例数与标准误:由式(8.10)与式(8.11)计算得
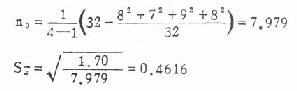
(3)列表比较:
表 8.7 均数间两两比较
| A 与 b (秩次) | 组数 a | ∣XA-XB∣ | 界 值 | P 值 | |
| q0.05Sχ | q0.01Sχ | ||||
| 4 与 3 | 2 | 1.01 | 1.36 | 1.86 | >0.05 |
| 4 与 2 | 3 | 2.15 | 1.65 | 2.14 | <0.01 |
| 4 与 1 | 4 | 4.39 | 1.83 | 2.32 | <0.01 |
| 3 与 2 | 2 | 1.14 | 1.36 | 1.86 | >0.05 |
| 3 与 1 | 3 | 3.38 | 1.65 | 2.14 | <0.01 |
| 2 与 1 | 2 | 2.24 | 1.36 | 1.86 | <0.01 |
注:本例组内均方的自由度为 28 但 q 值表中左侧无 28,故用邻近的较小自由度 20,此外也可用内插法求出 γ 为 28 的 q 值。
比较结果,除患移植性白血病甲、乙组间;甲组与自发性白血病组间(即按均数大小秩次 3 与 4、3 与 2 间)相差不显著外,余均在 α =0.01 水准处相差显著,说明正常鼠脾 DNA 含量最高,患移植白血病乙组的最低。
第三节 随机单位组设计资料的方差分析
随机单位组设计资料和 t 检验中的成对资料相类似,不同之处是成对资料只二个组,而随机单位组设计有三个或更多的组,因而要比较的均数多于两个,它是比完全随机设计更精细的一种设计方法。这样设计的资料作方差分析的检验效能较高,因为在此种设计的方差分析表中多了一个分析内容──单位组间的变异,致使误差均方有一定程度的缩小。下面用例子说明分析过程。
例 8.3 以缺乏核黄素的饲料喂大白鼠,一周后测尿中氨基氮的三天排出量,并与限食量组和不限食量组对比,结果见表 8.8,试比较三组均数间有无显着差别。
表 8.8 三组白鼠在进食一周后尿中氨基氮的三天排出量(mg)
| 单位组号 | 核黄素缺乏组 | 限食量组 | 不限食量组 | 小计 | x |
| 1 | 5.98 | 3.32 | 8.16 | 17.46 | 5.820 |
| 2 | 3.63 | 3.39 | 5.57 | 12.59 | 4.197 |
| 3 | 2.40 | 2.66 | 5.25 | 10.31 | 3.437 |
| 4 | 4.68 | 3.33 | 7.32 | 15.33 | 5.110 |
| 5 | 3.81 | 2.73 | 6.76 | 13.30 | 4.433 |
| 6 | 7.03 | 5.13 | 5.13 | 17.29 | 5.763 |
| 7 | 4.71 | 3.36 | 5.07 | 13.14 | 4.380 |
| 8 | 4.69 | 4.29 | 4.62 | 13.60 | 4.533 |
| 9 | 3.91 | 3.18 | 9.26 | 16.35 | 5.450 |
| 10 | 6.51 | 8.45 | 11.46 | 26.42 | 8.807 |
| 11 | 8.67 | 7.12 | 9.91 | 25.70 | 8.567 |
| 12 | 3.40 | 2.55 | 4.00 | 9.95 | 3.317 |
| ∑X | 59.42 | 49.51 | 82.51 | 191.44 | – |
| x | 4.952(2) | 4.126(3) | 6.876(3) | 5.318 | — |
| ∑X2 | 329.1142 | 242.8543 | 629.1065 | 1201.0748 | – |
离均差平方和:
总计:1201.0748-(191.44)2/36×183。0394
饲料组间
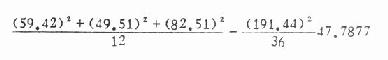
单位组间
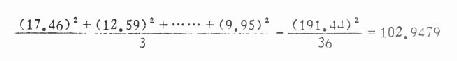
误差 183.0394-47.7877-102.9479=32.3038
注:以上分母 12 与 3 等为组内动物数。
表 8.9 方差分析表
| 方差来源 | 自由度 | 离均差平方和 | 均 方 | F | F0.01(v1,v2) |
| 总计 | 35 | 183.0394 | |||
| 饲料组间 | 2 | 47.7877 | 23.8939 | 16.27 | 5.72 |
| 单位组间 | 11 | 102.9479 | 9.3589 | 6.37 | 3.18 |
| 误差 | 22 | 32.3038 | 1.4684 |
表 8.8 是按饲料和单位组两个方面分组的资料,设计这种实验时,先将条件基本相同的实验对象组成单位组,然后将一个单位组内的实验对象随机分配到各处理组(饲料组)中去,每组一个。如本例先挑选同窝、同性别、体重基本相等的大白鼠三头,组成一个单位组,共组成 12 个单位组,然后将每一单位组的三头白鼠随机分配到三个饲料组中去,这样,每个处理组的重复数就是单位组数。表 8.8 与表 8.1 资料不同的地方是,表 8.1 在同一批内的各数值,位置可任意调动,不影响分析的结果,而表 8.8 内,需移动数据时必须把该横行(第 i 个单位组)的所有数值同时移动,才使分析结果不受影响。
表 8.9 中各个离均差平方和的数字来自表 8.8 下方。如果是完全随机设计资料的方差分析,分析表中并无单位组间这一横行的数字, 其自由度与离均差平方和被分别包含在原组内(误差)项中,就本例而言那么组内均方将为(102.9479+32.3038)/(11+22)=4.0985,比现在从分析表中看到的误差均方 1.4684 要大得多,也即求 F 值时分母要大得多。分母大,求出的 F 就小,那么在有的资料里就有可能使求得的 F 值不显著而改变结论,由此可见把“单位组间”均方从“组内”均方中分离出来的必要性。但假如在按两个标志分组的资料里,“单位组间”无显著相差,那么这部分均方不分离出来而仅有“组内”均方也可,而若没有这一部分,表 8.9 就会和表 8.2 的项目一样了。本资料不论“饲料组间”、“单位组间”所求 F 值均大于 F 0.01(1,2),故不同饲料组均数间在 α =0.01 水准处相差显著,各单位组平均数间也在 α =0.01 水准处相差显著。
由于三个饲料组均数间相差显著,我们用最小显著差数法进一步作了均数间的两两比较,见表 8.10,计算最小显著差数时用公式(8.8)、(8.9),得:
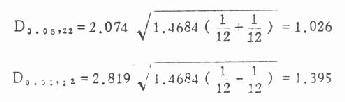
表 8.10 均数间两两比较
| A 与 B (秩次) | ∣XA-XB∣ | 界 值 | P 值 | |
| D0.05 | D0.01 | |||
| 3 与 2 | 0.826 | 1.026 | 1.395 | >0.05 |
| 3 与 1 | 2.750 | 1.026 | 1.395 | <0.01 |
| 2 与 1 | 1.924 | 1.026 | 1,395 | <0.01 |
秩次见表 8.8 内 X 一行括号内数字。
结论为不限食量组氨基氮三天排出量最高,至于核黄素缺乏组与限食量组之间,则尚未看出有显著差别。
再看表 8.8 右侧 12 个单位组的均数,经 F 检验已知相差显著,初步看第 10、11 号两个单位组的均数(分别为 8.807 和 8.567)比较高,其余的均在 3 与 6 之间差别不大。若作两两比较将要比较![]() 次(12 中取 2 的组合数),为免去许多麻烦,先取 10 号
次(12 中取 2 的组合数),为免去许多麻烦,先取 10 号
与 11 号比,若无显著相差可作为一类,再取 11 号均数与其最接近的第 1 号单位组均数相比,若相差显著,11 号均数就不必再与相差更大些的其它均数比下去了,现将这三者相比如下。
![]()
第 10 与第 11 号,均数之差为 8.807-8.567=0.240,小于 2.052,P>0.05
第 11 号与第 1 号 均数之差为 8.567-5.820=2.747, 大于 2.052,P<0.05。结果 10 号与 11 号单位组均数间无显著相差,而这两组与其余 10 组均相差显著,因为 1 号与 11 号相差 2.747 已差别显著,其余各组与 10、11 号差得更多,大概不会相差不显著的。可见,第 10、11 号两个单位组的动物尿中氨基氮较高。以上分析虽较简略,一般已可说明问题,因本资料的主要分析目的在于饲料组间的比较而并非单位组间。又假如表 8.9 的方差分析结果,F 小于临界值,说明均数间相差不显著,就不必考虑作均数间两两比较。
第四节 拉丁方设计资料的方差分析
表 8.11 家兔注射某种药物后不同部位所生疱疹大小(cm2)
| 动物编号 | 注射次序 | 各动物 小 计 | 各动物 平均数 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||||
| Ⅰ | B7.5 | C6.7 | A7.9 | D6.1 | F7.3 | E6.9 | 41.4 | 7.07 | |||
| Ⅱ | E8.5 | D8.2 | B8.1 | C9.9 | A8.7 | F8.3 | 51.7 | 8.62 | |||
| Ⅲ | C7.3 | F7.3 | E6.8 | A7.4 | B6.0 | D7.7 | 42.5 | 7.08 | |||
| Ⅳ | A7.4 | E7.7 | C6.4 | F5.8 | D7.1 | B6.4 | 40.8 | 5.80 | |||
| Ⅴ | F6.4 | B6.2 | D8.1 | E8.5 | C6.4 | A7.1 | 42.7 | 7.12 | |||
| Ⅵ | D5.9 | A8.2 | F7.7 | B7.5 | E8.5 | C7.3 | 45.1 | 7.52 | |||
| 各次小计 | 43.0 | 44.3 | 45.0 | 45.2 | 44.0 | 43.7 | 265.2 | ||||
| 部 位 小 计 | |||||||||||
| A | B | C | D | E | F | ||||||
| 46.7 | 41.7 | 44.0 | 43.1 | 46.9 | 42.8 | ||||||
例 8.4 下面的表 8.11 是家兔在不同部位注射某种药物后所生疱疹的大小。家兔共有六只,其编号为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ。注射部位有六处,其代号为 A、B、C、D、E、F,其中 A、B、C 在脊椎附近,D、E、F 在两侧,注射次序用 1、2、3、4、5、6 来表示。该表的读法是,第一次注射时 1 号兔在部位 B 处注射,所生疱疹大小为 7.5 平均厘米;Ⅱ号兔在部位 E 处注射,所生疱疹大小为 8.5 平方厘米;余类推。这里我们看到,这个资料是按家兔编号、注射部位、注射次序三个标志来分组的。这种分组与一般的按三个标志的分组(如性别、年龄、病型)又不一样,而是按特殊的实验设计安排的。这种实验设计叫做拉丁方设计。在表 8.11 里,我们看到三个分组标志各分六组,而且每次注射时(纵行)没有相同的部位,每个动物(横行)也没有重复的部位,所以拉丁方的同一纵行内与同一横行内没有相同的字母,这是拉丁方设计的要求。这种设计既控制了动物的个别差异,也控制了因注射日期(次序)不同而可能产生的差异,因此拉丁方的设计控制得更为严密,常用的拉丁方见附表 10。计算离均差平方和:
总计:(7.52+8.52+7.32+………+7.12+7.32)-(265.2)2/36=30.36
先求校正数 C=(265.2)2/36=1953.64
动 物 间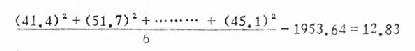
注射次序间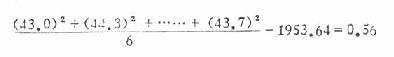
部 位 间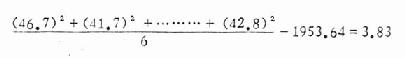
误 差 30.36-12.83-0.56-3.83=13.14
表 8.12 家兔疱疹资料的方差分析
| 方差分析 | 自由度 | 离均差平方和 | 均方 | F |
| 总计 | 35 | 30.36 | ||
| 动物间 | 5 | 12.83 | 2.566 | 3.91* |
| 注射次序间 | 5 | 0.56 | 0.112 | — |
| 部位间 | 5 | 3.83 | 0.766 | 1.17 |
| 误差 | 20 | 13.14 | 0.657 |
分析资料时,先求出各次注射、各家兔、各部位的小计,然后计算校正数及各离均差平方和与相应的自由度,列入方差分析表,以自由度除对应的离均差平方和,得均方。计算 F 时分母一律用误差项均方。这里注射次序间的均方小于误差均方,就不需要计算 F 值。查 F 值表,当 ν 1=5,ν2=20 时,F0.05(5,20)=2.71,部位间的 F 值小于 2.71,因此差别不显著,动物间的 F 值大于 F 0.05(5,20),故各家兔所生疱疹大小的六个平均数在 α =0.05 的水准处相差显著,下面将六个平均数进一步作两两比较:
从表 8.11 右侧六个动物的平均值看,Ⅱ号动物平均值为 8.62,最高,其次是Ⅵ号动物的 7.52,这两个均数比较后决定是否再和别的几个比。仍用最小显著差数法,先求出
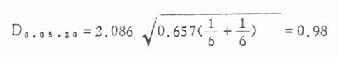
现 8.62-7.52=1.10>D0.05,20=0.98,故Ⅱ号与Ⅵ号动物在 α =0.05 水准处相差显著。Ⅱ号与其它各号动物的差别更大。下面查临界 q 值,比次大均数与最小均数即Ⅵ号的 7.52 与Ⅳ号的 5.80,相差为 1.72,与相应的![]() 比较时,均数的相差数大于临界值,相差显著。其它各号动物均数之间则因差别都很小,可不必比较。总之,六个动物间以Ⅱ号动物的均数最大,Ⅳ号的最小,与其余几个都差别显著,其它两两间无显著相差。
比较时,均数的相差数大于临界值,相差显著。其它各号动物均数之间则因差别都很小,可不必比较。总之,六个动物间以Ⅱ号动物的均数最大,Ⅳ号的最小,与其余几个都差别显著,其它两两间无显著相差。
第五节 几个方差的齐性检验
进行上述方差分析时,我们把比较的几个组的资料,看成是从几个相应的总体中随机抽取的独立样本,理论上要求几个总体都呈正态分布,几个总体的方差都是相同的,但总体均数可以不等。因此实际应用时,如果各组资料呈显着偏态,或各组方差相差悬殊,(尤其当各样本的含量甚不相同时)就不能用上述方法进行方差分析,而宜改用非参统计等其他方法比较多个样本均数。关于资料的正态性检验可看七章三节,关于各方差是否一致,现以表 8.5 资料为例将方差齐性检验的 Bartlett 氏法简述如下:
首先,作检验假设:样本来自方差相等的各总体,就本例言即
H:σ12=σ22=σ32=σ42
H1:各总体方差不尽相
α=0.05
然后按下列公式求检验统计量。如果检验假设属真,此统计量近似于自由度为 K - 1 的 X 2分布。各样本方差相差越大时求出的 X 2统计量也越大,反之则的反是。
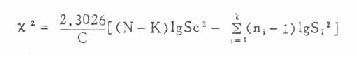
上式中 2.3026 是由自然对数换成常用对数计算时用的转换系数,若直接用自然对数 ln,不用 1g,就不必乘此数,C 也是一个系数,用以校正 χ 2值,求 C 的公式是,
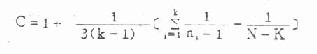
现不防先求 C 以便计算校正的 χ 2值,表 8.5 中各组的例数为 n 1=8,n2=7,n3=9,n4=8,K 组共计例数 N =32,则
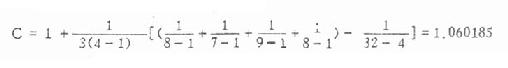
在表 8.5 的下部最末一行我们已将各组离均差平方和及其合计列出,只要分别除以各自的自由度即为各组方差及合并方差 S c2, 然后代入式 8.12 便可求得 χ 2

此值小于 X 20.05,3=7.81,P>0.05, 我们按 α =0.05 水准接受各总体方差相等的假设,认为方差是齐的。因此,该资料符合要求,可以进行方差分析来比较四组鼠脾 DNA 含量相差是否显著。
练习题
1.用三种抗凝剂(A1、A2、A3)对一血标本作红细胞沉降速度(一小时值)测定,每种各作 5 次,问用三种抗凝剂所作血沉值之间有差别否?
A1:15 11 13 12 14
A2:13 16 14 17 15
A3:13 15 16 14 12
2.下表所列数字为鹿茸草对五例原发性血小板减少症患者(治前血小板低于 10 万 /mm3)治疗一、二疗程及出院时的血小板升高数,另有五名健康成人用同一药物后不同时间的升高数附后。考虑这两个资料应用什么方法分析为宜,两者是否该用同一方法处理。
不同人用鹿茸草后血小板的升高值(万 /mm3)
| 患者号 | 一疗程后 | 二疗程后 | 出院时 | 健康人 | 用药后 | ||
| 二小时 | 五小时 | 一昼夜 | |||||
| 1 | 6.8 | 7.6 | 7.6 | 1 | 1.8 | 8.7 | 2.3 |
| 2 | 8.0 | 10.0 | 10.0 | 2 | 5.4 | 9.8 | 3.1 |
| 3 | 5.8 | 12.8 | 11.6 | 3 | 6.1 | 2.3 | 1.0 |
| 4 | 5.0 | 5.0 | 7.0 | 4 | 1.5 | 3.2 | 0.4 |
| 5 | 6.0 | 10.0 | 22.8 | 5 | 2.4 | 7.2 | 0.5 |
3.为测定黄铜铸造车间的空气中氧化锌浓度,在车间内选 4 个不同地点 A、B、C、D,每点取自地面不同的四个高度,于一日内的四个不同时间采用 4×4 拉丁方设计进行采样,用双硫腙比色法测定其含量,得结果如下。试比较不同地点、不同高度,不同时间车间空气中 ZnO 浓度有无显著不同。
不同地点、时间和高度空气中氧化锌浓度
| 采样时间(小时) | 氧化锌浓度 | |||
| 高度 1 | 高度 2 | 高度 3 | 高度 4 | |
| 9:00 | C10.5 | D7.7 | B12.0 | A13.2 |
| 11:00 | B11.1 | A12.0 | C10.3 | D7.5 |
| 14:00 | D5.8 | C12.2 | A11.2 | B13.7 |
| 17:00 | A11.6 | B12.3 | D5.9 | C10.2 |
第八章 直线相关与回归
前面各章介绍的统计方法都只涉及单一变量,即或进行两组或多组比较,所比较的仍然是同一变量,而且是以讨论各组间该变量的相差是否显着为中心环节。但医学领域里常可在一个统一体中遇到两个或多个变量之间存在着相互联系、相互制约的情况,如同一批水样的浊度与透光率,同一批人的年龄与血压以及身长、体重与胸围等。因而研究问题的方法就需要扩展。在统计方法中通常是用相关与回归的方法来研究不同变量之间的这种相互依存和互为消长的关系。相关与回归的种类较多,本章所涉及的只是其中最简单的直线相关与直线回归,简称相关与回归。
相关与回归即有区别又有联系,表达事物或现象间的在数量方面相互关系的密切程度用相关系数;说明一变量依另一变量的消长而变动的规律用回归方程。现先介绍相关,再介绍回归。
第一节 直线相关
一、相关系数的意义
相关分析是用相关系数(r)来表示两个变量间相互的直线关系,并判断其密切程度的统计方法。相关系数 r 没有单位。在 -1~+ 1 范围内变动,其绝对值愈接近 1,两个变量间的直线相关愈密切,愈接近 0,相关愈不密切。相关系数若为正,说明一变量随另一变量增减而增减,方向相同;若为负,表示一变量增加、另一变量减少,即方向相反,但它不能表达直线以外(如各种曲线)的关系。
为判断两事物数量间有无相关,可先将两组变量中一对对数值在普通方格纸上作散点图,如图 9.1~9.8 所示。图中点子的分布可出现以下几种情况:
正相关——见图 9.1,各点分布呈椭圆形,Y 随 X 的增加而增加,X 亦随 Y 的增加而增加,此时 1 >r>0。椭圆范围内各点的排列愈接近其长轴,相关愈密切,当所有点子都在长轴上时,r=1(见图 9.2),称为完全正相关。
负相关——见图 9.3,各点分布亦呈椭圆形,Y 随 X 的增加而减少,X 也随 Y 的增加而减少,此时 0 >r>-1。各点排列愈接近其长轴,相关愈密切,当所有点子都在长轴上时,r=1(见图 9.4),称为完全负相关。
在生物现象中,完全正相关或完全负相关甚为少见。
无相关——见图 9.5、图 9.6 和图 9.7,X 不论增加或减少,Y 的大小不受其影响;反之亦然。此时 r =0。另外,须注意有时虽然各点密集于一条直线,但该直线与 X 轴或 Y 轴平行,即 X 与 Y 的消长互不影响,这种情况仍为无相关。
非线性相关——见图 9.8,图中各点的排列不呈直线趋势,却呈某种曲线形状,此时 r≈0,类似这种情况称为非线性相关。
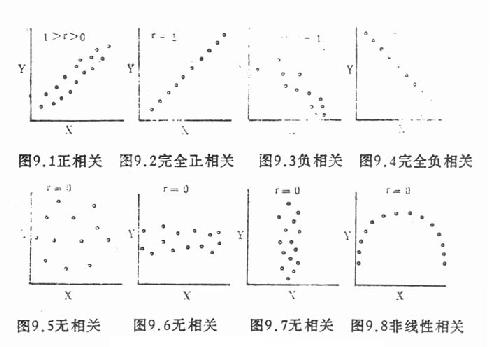
图 9.1—9.8 不同相关系数的散点示意图
二、相关系数的计算及假设检验
(一)相关系数计算法
计算相关系数的基本公式为:
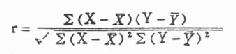 (9.1)
(9.1)
式(9.1)中 r 为相关系数,∑(X-X)2为 X 的离均差平方和,∑(Y-Y)2为 Y 的离均差平方和,∑(X-X)(Y-Y)为 X 与 Y 的离均差乘积之和,简称离均差积之和,此值可正可负。以此式为基础计算相关系数的方法称积差法,在实际应用时式(9.1)中各离均差平方和(简称差方和)与积之和可化为
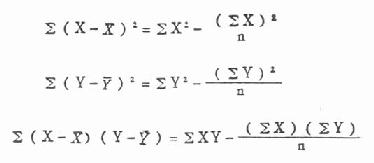
(9.2)
现举例说明计算相关系数的一般步骤:
例 9.1 测定 15 名健康成人血液的一般凝血酶浓度(单位 / 毫升)及血液的凝固时间(秒),测定结果记录于表 9.1 第(2)、(3)栏,问血凝时间与凝血酶浓度间有无相关?
1.绘图,将表 9.1 第(2)、(3)栏各对数据绘成散点图,见图 9.9。
2.求出∑X、∑Y、∑X2、∑Y2、∑XY,见表 9.1 下方。
3,代入公式,求出 r 值。
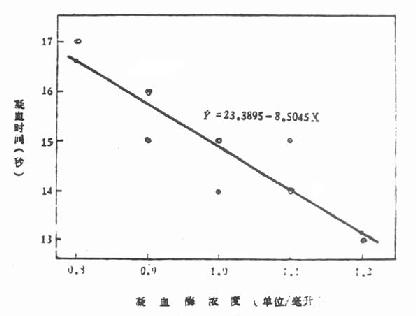
图 9.9 凝血时间与凝血酶浓度散点图及回归直线
表 9.1 相关系数计算表
| 受试者号 (1) | 凝血酶浓度(单位 / 毫升)X(2) | 凝血时间(秒)Y(3) |
| 1 | 1.1 | 14 |
| 2 | 1.2 | 13 |
| 3 | 1.0 | 15 |
| 4 | 0.9 | 15 |
| 5 | 1.2 | 13 |
| 6 | 1.1 | 14 |
| 7 | 0.9 | 16 |
| 8 | 0.9 | 15 |
| 9 | 1.0 | 14 |
| 10 | 0.9 | 16 |
| 11 | 1.1 | 15 |
| 12 | 0.9 | 16 |
| 13 | 1.1 | 14 |
| 14 | 1.0 | 15 |
| 15 | 0.8 | 17 |
| 合计 | 15.1 | 222 |
∑X=15.1 ∑Y=222
∑XY=221.7
∑X2=15.41∑Y2=3304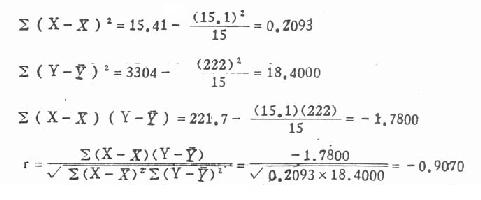
本例的相关系数 r =-0.9070,负值表示血凝时间随凝血酶浓度的增高而缩短;绝对值∣-0.9070∣表示这一关系的密切程度。至于此相关系数是否显著,则要经过下面的分析。
(二)相关系数的假设检验
虽然样本相关系数 r 可作为总体相关系数 ρ 的估计值,但从相关系数 ρ = 0 的总体中抽出的样本,计算其相关系数 r,因为有抽样误差,故不一定是 0,要判断不等于 0 的 r 值是来自 ρ = 0 的总体还是来自 ρ≠0 的总体,必须进行显著性检验。检验假设是 ρ =0,r 与 0 的差别是否显著要按该样本来自 ρ = 0 的总体概率而定。如果从相关系数 ρ = 0 的总体中取得某 r 值的概率 P >0.05,我们就接受假设,认为此 r 值的很可能是从此总体中取得的。因此判断两变量间无显著关系;如果取得 r 值的概率 P≤0.05 或 P≤0.01,我们就在 α =0.05 或 α =0.01 水准上拒绝检验假设,认为该 r 值不是来自 ρ = 0 的总体,而是来自 ρ≠0 的另一个总体,因此就判断两变量间有显著关系。
由于来自 ρ - 0 的总体的所有样本相关系数呈对称分布,故 r 的显著性可用 t 检验来进行。本例 r =-0.9070,进行 t 检验的步骤为:
1.建立检验假设,H:ρ=0,H1:ρ≠0,α=0.01
2.计算相关系数的 r 的 t 值:
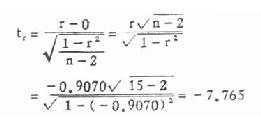 (9.3)
(9.3)
3.查 t 值表作结论
ν=n-2=15-2=13
根据专业知识知道凝血酶浓度与凝血时间之间不会呈正相关,故宜用单侧界限,查 t 值表得
t0.01,13=2.650
今∣tr∣>t0.01,13,P<0.01,在 α =0.01 水准上拒绝 H,接受 H 1,故可认为凝血时间的长短与血液中酶浓度有负相关。
为简化 t r检验的计算过程,数理统计工作者根据 t 分配表,已把不同自由度时 r 的临界值求出,并列成相关系数界值表(见附表 11)。故求相关系数后,只需查表就可知道该 r 值是否显著,而不必再计算 t r值。
r 的显著性界限为
|r|<r0.05,ν P>0.05 相关不显著 </r
r0.05,,≤|r|<r0.01,,0.05≥P>0.01
在 α =0.05 水准上相关显著
|r|≥r0.01,,P≤0.01 在 α =0.01 水准上相关显著
例 9.1 的 ν =15-2=13,查附表 11 中 P (1)的界值,得:
r0.05,13=0.441r0.01,13=0.592
现 r =-0.9070,∣r∣>r0.01,13,P<0.01, 按 α =0.01 水准,拒绝 H O, 接受 H 1。认为 ρ≠0,说明凝血时间的长短与血液中凝血酶浓度有负相关。结论与计算所得一致。
相关系数的显著性与自由度的大小有关,如 n =3,ν= 1 时,虽 r =-0.9070,却为不显著;若 ν =400 时,即使 r =0.1000,亦为显著。因此不能只看 r 的值,不考虑 ν 就下结论。
第二节 直线回归
一、直线回归方程的意义
计算出相关系数后,如果 r 显着,且又需要进一步了解两变量中一个变量依另一个变量而变动的规律时,则可进行回归分析。
“回归”是个借用已久因而相沿成习的名称。若某一变量(Y)随另一变量(X)的变动而变动,则称 X 为自变量,Y 为应变量。这种关系在数学上被称为 Y 是 X 的函数,但在医学领域里,自变量与应变量的关系和数学上的函数关系有所不同。例如成年人年龄和血压的关系,通过大量调查,看出平均收缩压随年龄的增长而增高,并且呈直线趋,但各点并非恰好都在直线上。为强调这一区别,统计上称这是血压在年龄上的回归。
直线回归分析的任务就是建立一个描述应变量依自变量而变化的直线方程,并要求各点与该直线纵向距离的平方和为最小。按这个要求计算回归方程的方法称为最小平方法或最小二乘法。所建立的方程是一个二元一次方程式,其标准形式是:
![]() =a+bX(9.5)
=a+bX(9.5)
式(9.4)![]() 为由 X 推算得来的 Y 值,即 Y 的估计值:a 称为截距,它是当 X = 0 时的
为由 X 推算得来的 Y 值,即 Y 的估计值:a 称为截距,它是当 X = 0 时的 ![]() 值,即回归直线与纵轴的交点:b 称为回归系数,它是回归直线的斜率,其含意是当 X 每增加一个单位时,
值,即回归直线与纵轴的交点:b 称为回归系数,它是回归直线的斜率,其含意是当 X 每增加一个单位时,![]() 相应增(或减)b 个单位。当 a 与 b 求得后,直线回归方程就确定了。
相应增(或减)b 个单位。当 a 与 b 求得后,直线回归方程就确定了。
二、直线回归方程的计算法
仍以表 9.1 资料为例,根据前面的相关分析以及医学上有关凝血的机理,可知凝血时间依凝血酶浓度而异,且有密切的关系。因此可进一步作由凝血酶浓度(X)推算凝血时间(Y)的回归方程。求直线回归方程的步骤如下:
1.列回归计算表(见表 9.1),计算∑X、∑Y、∑X2、∑Y2、∑XY。
2.计算 X、Y、∑(X-X)2、∑(X-X)(Y-Y)
X=∑X/n=15.1/15=1.01
Y=∑Y/n=222/15=14.80
∑(X-X)2=∑X2-(∑X)2/n=0.2093
∑(X-X)(Y-Y)=∑XY-∑X·∑Y/n=-1.7800
3.计算回归系数 b 和截距 a。b 和 a 两值计算公式均是根据最小二乘法的原理推算出来的,其公式如下:
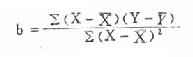 (9.5)
(9.5)
a=Y-bX(9.6)
本例 b =-1.7800/0.2093=-8.5045
a=14.80-(-8.5045)(1.01)=23.3895
4.列出回归方程,绘制回归直线,将求得的 b 和 a 的值代入到式(9.4),即得所求的回归方程:
![]() =23.3895-8.504X
=23.3895-8.504X
在凝血酶浓度的实测范围内,即 X =0.8 到 X =1.2 之间,任选两个 X 值(一般选相距较远且直角坐标系上容易读出者),代入此回归方程,即得相应的两个![]() 值。例如:
值。例如:
取 X1=0.8,则![]() 1=23.3895-8.5045×0.8=16.59,
1=23.3895-8.5045×0.8=16.59,
X2=1.2 则![]() 2=23.3895-8.5045×1.2=13.18。
2=23.3895-8.5045×1.2=13.18。
连接(0.8、16.59)和(1.2、13.18)两点所得直线,即为由凝血酶浓度推算凝血时间的回归直线(见图 9.9)。须注意回归直线必通过(χ,y)点,并穿过观察点群,直线上下各有一些点散布着,否则计算有误。
三、直线回归方程的假设检验
(一)样本回归系数的假设检验
根据例 9.1 资料求得的是样本回归系数 b,有抽样误差的,需作假设检验,检验其是否是从回归系数为 0 的假设总体(即 β =0)中随机抽得的,也就是检验 b 与 0 的差别有无显着性。如果差别有显着性,可认为 X 与 Y 间有直线回归存在。
样本回归系数的假设检验亦用 t 检验。
H:β= 0 即 Y 的变化与 X 无关;
H1:β≠0。
计算公式为:
![]() (9.7)
(9.7)
分母 S b是样本回归系数 b 的标准误,计算公式为:
![]() (9.8)
(9.8)
分子 Sy.x 为各观察值 Y 距回归线的标准差,即当 X 的影响被扣去以后 Y 方面的变异,可按下式计算:
![]() (9.9)
(9.9)
式中∑(Y-![]() )2为估计误差平方和,常用下式计算:
)2为估计误差平方和,常用下式计算:
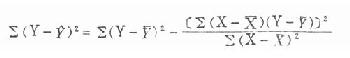 (9.10)
(9.10)
根据数理统计的理论,同一批资料计算所得 t r与 t b是相同的,即 t r=tb。处理资料时可检验相关显著性代替其回归显著性。
由于例 9.1 资料的 r 在 α =0.01 水准上显著,故可判断样本回归系数 -8.5045 与 0 的相差有显著性,说明存在凝血时间随凝血酶浓度变化而变化的回归关系。
(二)两样本回归系数相差的假设检验
若有两个可以比较的样本,它们的回归系数分别为 b 1与 b 2,经检验都为显著,回归系数的标准误分别为 S b1和 S b2。b1与 b 2相差的显著性也可用 t 检验法检验,其计算公式为:
![]() (9.11)
(9.11)
ν=n1+n2-4
式(9.11)中 S b1-b2为两样本回归系数之差的标准误,其计算公式为:
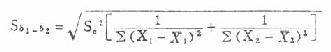 (9.12)
(9.12)
式(9.12)中 S 2C为两样本回归系数的合并方差,其计算公式为:
![]() (9.13)
(9.13)
式(9.13)中∑(Y-![]() )2为估计误差平方和,即观察值 Y 与估计值
)2为估计误差平方和,即观察值 Y 与估计值 ![]() 的差数(Y-
的差数(Y-![]() )的平方之和。其计算公式见公式(9.10),
)的平方之和。其计算公式见公式(9.10),
现以实例说明两样本回归系数 t 检验的步骤。
例 9.2 表 9.2 资料为同一批白蛋白于 38℃与 25℃条件下,不同时间(分)的凝固百分比,问由此而得的两样本回归系数相差是否显著?
表 9.2 白蛋白在两种温度下各不同时间的凝固百分比
| 时间(分) | 凝固百分比(%) | |
| X | 25℃Y1 | 38℃Y2 |
| 3 | 7.2 | 12.0 |
| 6 | 18.4 | 30.0 |
| 9 | 30.0 | 44.0 |
| 12 | 40.0 | 53.0 |
| 15 | 49.0 | 66.0 |
| 18 | 58.0 | 81.5 |
| 合计 63 | 202.6 | 286.5 |
本例图示见图 9.10,本例计算见图下:
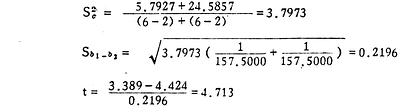
图 9.10 白蛋白在两种温度下各不相同时间的凝固百分比
r1=0.998(P<0.01) b1=3.389∑(Y1–![]() 1)2=5.7927n1=6
1)2=5.7927n1=6
r2=0.996(P<0.01) b2=4.424∑(Y2–![]() 2)2=24.5857n2=6
2)2=24.5857n2=6
∑(X1-X1)2=∑(X2-X2)2=157.5000
1.H:β1-β2=0
H1:β1-β2≠0
α=0.01
2.计算 t 值:
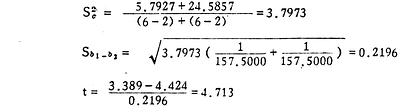
3.查 t 值表作结论:以 ν =6+6-4= 8 查 t 值表,得
t0.01,8=2.355, 今∣t∣>t0.01,8, 故 P <0.01。
4.判断结果:按 α =0.01 水准,拒绝 H,接受 H 1,故两个回归系数差别显著。说明两条回归直线的斜率不同,两条回归直线中 X 对 Y 的影响规律不一致。现 b 2>b1,说明随着时间的增加,蛋白质在 38℃时凝固百分比的增加量比在 25℃时高。
第三节 计算相关与回归的注意事项
1.作相关与回归分析要有实际意义。不要把毫无关联的两个事物或现象用来作相关或回归分析。如儿童身高的增长与小树的增长,作相关分析是没有实际意义的,如果计算由儿童身高推算小树高的回归方程则更无实际意义。也许算得的 r、b 是显着的,也是没有意义的。
2.对相关分析的作用要正确理解。相关分析只是以相关系数来描述两个变量间相互关系的密切程度和方向,并不能阐明两事物或现象间存在联系的本质。而且相关并不一定就是因果关系,切不可单纯依靠相关系数或回归系数的显着性“证明”因果关系之存在。要证明两事物间的因果关系,必须凭籍专业知识从理论上加以阐明。但是,当事物间的因果关系未被认识前,相关分析可为理论研究提供线索。
3.相关与回归的区别和联系:相关表示两变量间的相互关系,是双方向的。而回归则表示 Y 随 X 而变化,这种关系是单方向的。医学资料中的有些资料用相关表示较适宜,比如兄弟与姐妹间的身长关系、人的身长与前臂长之间的关系等资料。另有些资料用相关和回归都适宜,此时须视研究需要而定。就一般计算程序来说,是先求出相关系数 r 并对其进行假设检验,如果 r 显著并有进行回归分析之必要,再建立回归方程。
回归系数与相关系数的正负号都有两变量离均差积之和的符号业决定,所以同一资料的 b 与其 r 的符号相同。回归系数有单位,形式为(应变量单位 / 自变量单位)相关系数没有单位。相关系数的范围在 -1~+ 1 之间,而回归系数没有这种限制。
4.适合作相关和回归分析的资料通常有两种资料:(1)一个变量 X 是选定的,另一个变 Y 是从正态分布的总体中随机抽取的,宜作回归分析。(2)两变量 X、Y(或 X 1、X2)都是从正态分布的总体中随机抽取的,即是正态双变量中的随机样本。这时,若需要由一个变量推算另一个变量可作回归分析;若只需说明两变量间的相互关系可作相关分析。如果变量(一个或两个)呈明显偏态时,须经过适当的变量代换(如对数代换等),使资料接受正态分布后再做相关与回归分析;或者采用秩相关法(见第十章第四节)。
5.在回归分析中,由 X 推算 Y 与由 Y 推算 X 的回归方程是不同的,不可混淆。
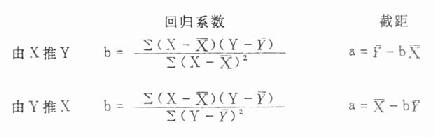
但我们必须正确选定自变量与应变量,一般说,事物的原因作自变量 X,当事物的因果关系不很明确时,选误差较小的即个体变异小的变量作自变量 X,以推算应变量 Y。
6.回归方程的适用范围有其限度,一般仅适用于自变量 X 的原数据范围内,而不能任意外推。因为我们并不知道在这些观察值的范围之外,两变量间是否也呈同样的直线关系。
练习题
1.测量了 10 个家庭中兄弟和姐妹的平均身长,试根据本资料的数据对兄弟与姐妹间身长进行相关分析。
| 家庭编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 合计 |
| 兄弟(厘米)X1 | 65 | 66 | 66 | 67 | 68 | 70 | 70 | 71 | 71 | 72 | 686 |
| 姐妹(厘米)X2 | 59 | 62 | 65 | 63 | 64 | 65 | 65 | 62 | 69 | 66 | 640 |
2.某研究组测定羊抗人血清 IgG 含量与沉淀圈直径,其测定结果如下。试据本资料的对数值作相关与回归分析。问能否用沉淀圈直径推算 IgG 含量?
羊抗人血清 IgG 含量(μg/μl)与沉淀圈直径(mm)
| 编号 | 真数 | 对数 | ||
| 羊抗人血清 IgGX | 沉淀圈直径 Y | 羊抗人血清 IgGX=1gX | 沉淀圈直径 Y =1gY | |
| 1 | 4.50 | 1.56 | 0.6532 | 0.1931 |
| 2 | 5.50 | 3.12 | 0.7404 | 0.4942 |
| 3 | 6.50 | 6.25 | 0.8129 | 0.7959 |
| 4 | 8.50 | 12.50 | 0.9294 | 1.0969 |
| 5 | 11.50 | 25.00 | 1.0607 | 1.3979 |
| 6 | 13.50 | 50.00 | 1.1303 | 1.6990 |
| 合计 | – | – | 5.3269 | 5.6770 |
3.有人测定了大白鼠正常肝与肝肿瘤中蛋白质的含量与逆甲氨酶的活度,得结果如下。试检验两样本回归系数 b 1与 b 2间有无显著相差。
两组肝中蛋白质含量与递甲氨酶活度
| 正常肝 | 肝肿瘤 | ||
| 蛋白质含量(mg)X1 | 酶活度(CPM)Y1 | 蛋白质含量(mg)X2 | 酶活度(CPM)Y2 |
| 0.39 | 16 | 0.94 | 198 |
| 0.69 | 27 | 1.00 | 310 |
| 0.90 | 40 | 0.50 | 101 |
| 1.20 | 67 | 1.70 | 563 |
| 1.35 | 61 | 0.80 | 376 |
| 1.60 | 88 | 0.33 | 75 |
| 6.13 | 299 | 5.27 | 1623 |
| n1=6 | n2=6 | ||
| b1=59.07 | b2=353.02 | ||
| Sb1=6.2664 | Sb2=78.1412 | ||
| ∑(X1– X1)2=0.9979 | ∑(X2-X2)2=1.1437 | ||
| ∑(Y1– | ∑(Y2– | ||
4.思考题
(1)要分析吸烟与否和肺癌发病率的关系应收集什么资料,用什么统计方法分析?
(2)若 r >r0.05可否得出 t b>t0.05的结论?
(3)若样本回归系数 b <0,可否认为两变量呈负相关?
(4)回归系数愈大,两变量关系是不是愈密切?
(5)∑(Y-![]() )2说明什么问题?
)2说明什么问题?
第十章 非参数统计
第一节 概念
什么叫非参数统计?先从参数统计说起。总体的特征值叫参数,一些特定分布都有其参数,如正态分布由 μ、σ 两个参数所决定。有些统计方法是根据特定分布设计出来的,如估计正常值范围的正态分布法、U 检验等是根据正态分布设计出来的,这样的一些方法统称为参数统计,前边已学过的 t 检验和方差分析都属于参数统计。但在实际工作中,有些资料不易判定或不符合所要求的分布,因此就需要有这样一些统计方法,它不受由参数所决定的特定分布的限制而适用于任意分布,这类统计方法称为非参数统计(non-parametric Statistics)或称不拘分布 distribution-free)的统计。
用非参数统计法处理资料时所比较的是分布而不是参数。它不考虑资料的分布类型,直接用样本数据的符号、大小顺序号、综合判断划分的名次、严重程度、优劣等级等作比较。
非参数统计的优缺点是:
方法简便、易学易用,要求资料所具备的条件不像参数法那样严格,因而易于推广使用。另外,参数法难以处理的等级资料,非参数法却能加以分析,故其应用范围广泛。
但如果已知资料所属总体近似于正态分布,或者资料经代换后可呈某种特定分布,那末,非参数统计法所得信息就不及参数统计法多,当检验假设错误时,非参数统计发现差异的灵敏度也较低。
当资料中例数并不太少时,用非参数统计所得的结论常和用参数统计法相同,但当统计结果在显著性界线附近时,两者结论可能不同,此时,若资料具备参数统计要求的条件,则以参数统计结论较合理,若资料不具备参数统计要求的条件,则非参数统计的结论可能准确些。
在下述情况下非参数统计可作为首选方法:
1.各种资料的初步分析;
2.某种标志不便准确的测量,而只能以严重程度、优劣等级、成效大小、名次先后或综合判断等方式定出次序时;
3.资料的分布类型不能确定时;
4.综合分析同质性较差的资料时,如不同地点,不同年份的某种实验结果等;
5.组内个别数据偏离过大,或各组内变异相差悬殊时。
第二节 符号检验
将资料用正负号表示,然后根据正负号个数计算 χ 2值进行假设检验,称为符号检验。符号检验的检验假设:若为成对资料,则为 H:P(X1>X2)=P(X2>X1),含义是总体内每一对数字(分别用 X 1和 X 2表示)中,X1>X2的概率等于 X 2>X1的概率,都是 1 /2,而备择假设 H 1为 P(X1>X2)≠P(X2>X1)≠1/2;若为不成对资料,检验假设 H 为 F(X1)=F(X2)即两总体的分布函数相等,而 H 1:F(X1)≠F(X2)。符号检验的计算都很简单,但检验效率也较低。
一、成对资料的比较
现以例 10.1 说明其计算步骤如下:
1.划出每对数值的正负号,如令用药后每分钟灌流滴数大于用药前的为“+”,反之为“-”,相等为“0”,则其结果见表 10.1 最右侧栏。
2.清点“+”、“-”、“0”各有几个,分别记为 n +、n–、n,得 n +=9,n-=3,n=0
3.代入式(10.1),求得 χ 2值
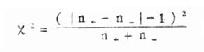 ,v=1(10.1)
,v=1(10.1)
4.但 χ 2值表,作出结论。
例 10.1 表 10.1 为豚鼠注入肾上腺素前后的每分钟灌流滴数,试比较给药前后灌流滴数有无显著差别。
表 10.1 豚鼠给药前后的灌流滴数
| 豚鼠号 | 每分钟灌流滴数 | X2-X1的正负号 | |
| 用药前 X 1 | 用药后 X 2 | ||
| 1 | 30 | 46 | + |
| 2 | 38 | 50 | + |
| 3 | 48 | 52 | + |
| 4 | 48 | 52 | + |
| 5 | 60 | 58 | – |
| 6 | 46 | 64 | + |
| 7 | 26 | 56 | + |
| 8 | 58 | 54 | _ |
| 9 | 46 | 54 | + |
| 10 | 48 | 58 | + |
| 11 | 44 | 36 | – |
| 12 | 46 | 54 | + |
将 n +=9,n–= 3 代入式 (10.1) 得
![]()
χ20.05,1=3.841, 今 χ 2<χ20.05,1, 故 P <0.05,不能拒绝检验假设 H,故这种相差是不显著的,不能得出用药后比用药前灌流滴数增加的结论。
此法简便,但较粗糙,数据少于 6 对时,不能测出显著性,12 对以下应慎用,当达到 20 对以上时,其结果才比较可靠,另外,n。较多时,会夸大差别。
二、不成对资料(两组或多组)的比较
现以例 10.2 说明其计算步骤如下:
1.各自排列,统一编秩号。将两组数据分别从小到大排列,然后按两组数据自小至大统一给以顺序号,即为秩号。编秩号时,凡数据相等而分属于两组的,应编平均秩号,如 0.042 共有三个,分属于两组,其秩号应该是 7、8、9,求其平均,皆给以平均秩号 8。
2.求秩号的中位数 M R,公式是:
 (10.2)
(10.2)
3.求各组 n +、n–、n:以 M R为准,大于 M R的秩号个数为 n +,小于 M R的秩号个数为 n –,相等者为 n。
4.代入下式求 χ 2值
![]() ν= 组数 -1(10.3)
ν= 组数 -1(10.3)
5.查 χ 2值表,作结论。
例 10.2 表 10.2 为 9 名健康人和 8 名铅作业工人的尿铅值(mg/L)试比较两组间有无显著差别?
表 10.2 9 名健康人与 8 名铅作业工人的尿铅值(mg/L)
| 健康人 | 秩号 | 铅作业工人 | 秩号 |
| 0.001 | 1 | 0.042 | 8 |
| 0.002 | 2 | 0.042 | 8 |
| 0.014 | 3 | 0.048 | 10 |
| 0.020 | 4 | 0.050 | 11 |
| 0.032 | 5 | 0.082 | 14 |
| 0.032 | 6 | 0.086 | 15 |
| 0.042 | 8 | 0.092 | 16 |
| 0.054 | 12 | 0.098 | 17 |
| 0.064 | 13 |
两组各自排队,统一编秩号,其结果见表 10.2
![]() 以此数为准,数得两组秩号的 n +、n–、n 如
以此数为准,数得两组秩号的 n +、n–、n 如
下:
| n+ | n– | n | |
| 健康人数 | 2 | 7 | |
| 铅作业工人组 | 6 | 2 |
代入公式
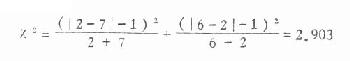
ν=2-1=1,χ20.05,1=3.841
今 χ 2<χ20.05,1故 P >0.05 不能拒绝检验假设,相差不显著,还不能说健康人与铅作业工人尿铅值有显著差别。
当多组资料比较时,其步骤与两组比较的一致,但计算 χ 2值的公式略有不同:
![]() (10.4)
(10.4)
符号检验未充分利用原始资料中的全部信息,故比较粗,但因其简便,可迅速得到结果故也有其使用价值。
第三节 秩和检验
用秩号代替原始数据后,所得某些秩号之和,称为秩和,用秩和进行假设检验即为秩和检验。其检验假设在两组比较(成对或不成对)时,H:F(X1)=F(X2),即两总体的分布函数相等,备择假设 H 1:F(X1)≠F(X2)。本法由于部份地考虑了数据的大小,故检验效力较符号检验大大提高。至于其方法、步骤,不论是查表法或计算法、也都相当简便,现举例说明如下。
一、成对资料的比较
此法由 Wilcoxon 氏首次提出,故又称 Wilcoxon 氏法。
处理时可用查表法或计算法,今以例 10.3 分别说明如下。
查表法步骤:
1.排队,将差数按绝对值从小至大排列并标明原来的正负号,见表 10.3 第(5)栏,排队后与原豚鼠号已无对应关系。
2.编秩号,成对资料编秩号时较为复杂,要注意三点:
(1)按差数的绝对值自小至大排秩号,但排好后秩号要保持原差数的正负号;
(2)差数绝对值相等时,要以平均秩号表示,如表 10.3 中差数绝对值为 4 者共三人,其秩号依次应为 2、3、4,现皆取平均秩号 3;
(3)差数为 0 时,其秩号要分为正、负各半,若有一个 0,因其绝对值最小,故秩号为 1,分为 0.5 与 -0.5,若有两个 0,则第二个 0 的秩号为 2,分为 1 与 - 1 等等。
3.求秩号之和即将正、负秩号分别相加,本例得正秩号之和为 68,负秩号之和为 10,正负秩号绝对值之和应等于 1 /2n(n+1),可用以核对,如本例 68+10=12/1(12+1)=78,证明秩号计算正确。
4. 以较小一个秩号之和(R),查附表 12 进行判断,该表左侧为对子数,表身内部是较小秩号和,与上端纵标目之概率 0.05,0.01 相对应,其判断标准是
R>R0.05时 P >0.05
R0.05≥R>R0.01时 0.05≥P>0.01
P≤R0.01时 P≤0.01
例 10.3 请以表 10.1 资料用秩和检验处理之。
表 10.3 豚鼠给药前后灌流滴数及其秩号
| 豚鼠号 (1) | 每分钟灌流滴数 | 按差数绝对值排队(5) | 秩号 | |||
| 用药前(2) | 用药后(3) | 差数(4) | 正(6) | 负(7) | ||
| 1 | 30 | 46 | 16 | -2 | 1 | |
| 2 | 38 | 50 | 12 | -4 | 3 | |
| 3 | 48 | 52 | 4 | 4 | 3 | |
| 4 | 48 | 52 | 4 | 4 | 3 | |
| 5 | 60 | 58 | -2 | -8 | 6 | |
| 6 | 46 | 64 | 18 | 8 | 6 | |
| 7 | 26 | 56 | 30 | 8 | 6 | |
| 8 | 58 | 54 | -4 | 10 | 8 | |
| 9 | 46 | 54 | 8 | 12 | 9 | |
| 10 | 48 | 58 | 10 | 16 | 10 | |
| 11 | 44 | 36 | -8 | 18 | 11 | |
| 12 | 46 | 54 | 8 | 30 | 12 | |
68 R=10
将表中 10.1 中用药前后的数据求出差数,并按差数绝对值排队,结果见表 10.3 第(5)栏。再编秩号,为计算方便,正、负秩号分列两栏,见表 10.3 第(6)、(7)栏。
上例,n=12,∣R∣=10,查附表 12 得
R0.05=14R0.01=7
今 R 0.05>R>R0.01,故 0.05>P>0.01,在概率 0.05 水平上拒绝 H,接受 H 1,即用药前后的相差是显著的,给药后每分钟灌流滴数比用药前增多了。
附表 12 中只列有 n≤25 时的临界值。当 n 值较大时亦可采用计算法。
计算法步骤:
在计算法时,对差数的排队,编秩号及求秩号之和同查表法,不同的是求得秩号之和以后的算,所用公式是:
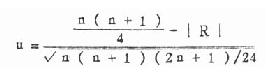
u0.05=1.96u0.01=2.58 (10.5)
式中 n 为原始资料中数据的对子数,R 为正秩号之和或负秩号之和,为计算方便,通常取绝对值较小的秩号之和为 r。
本例,n=12,R=-10,代入得:
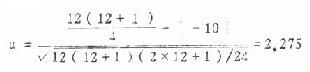
U0.05<u<0.01,故 0.05>P>0.01,在 α =0.05 水准上拒绝 H,接受 H1,结论与查表法相同。</u<
据研究,当 n 大于 10 时,上式算得的 u 近似正态分布,故计算法只用于 n 值较大时。
因本例资料接近正态分布,故曾用 t 检验的个别比较方法处理过,结果是:t=2.653 0.05>P>0.01,与秩和检验结论相同,但与符号检验结论不同(χ2=2.083,P>0.05),说明符号检验的检验效率比秩和与 t 检验都要低,比较粗糙,而秩和检验的效率与 t 检验较接近。
二、两组资料的比较
此法又称为 wilcoxon 氏两样本法。
处理时也可用查表法或计算法,今以例 10.4 分别说明之。
查表法步骤:
1.各自排队,统一编秩号,即将两组数据分别从小到大排列,但编秩号时要两组统一进行,凡分属于两组的相等数据用平均秩号,如本例 0.042 共三个,取平均序号皆为 8。
2.令较小样本秩号之和为 r,例数为 n 1。
3.计算 R',公式为:
R'=n1(n1+n2+1)-r (10.6)
R'是同一个样本资料,当秩号倒排(即由大至小)时较小样本秩号之和。
4.以 R 和 R'两秩号之和中较小者与附表 13 中 R 的临界值比较,以作出判断,其标准仍是:
R>R0.05时 P>0.05
R0.05≥R>R0.01时 0.05≥P>0.01
P≤R0.01时 P≤0.01
例 10.4 请以表 10.2 资料用本法处理之。
表 10.4 九名健康人与八名铅作业工人的尿铅值(mg/L)
| 健康人 | 秩号 | 铅作业工人 | 秩号 |
| 0.001 | 1 | 0.042 | 8 |
| 0.002 | 2 | 0.042 | 8 |
| 0.014 | 3 | 0.048 | 10 |
| 0.020 | 4 | 0.050 | 11 |
| 0.032 | 5 | 0.082 | 14 |
| 0.032 | 6 | 0.086 | 15 |
| 0.042 | 8 | 0.092 | 16 |
| 0.054 | 12 | 0.098 | 17 |
| 0.064 | 13 | ||
| n2=9 | 54 | n1=8 | R=99 |
先将本表 10.2 中两组数据各自排队并统一编秩号,结果见表 10.4。
较小样本为铅作业工人组,n1=8,R=99,代入式(10.6)
R'=8(8+9+1)-99=45
R 与 R'两者中以 R'较小,故以 P'值与附表 13 数值比较,得 R 0.05=51,R0.01=45;今 R'=R0.01,故 P =0.01,在 α =0.05 水平上拒绝 H,接受 H 1,差别显著,故铅作业工人尿铅值比健康人高。
计算法步骤:
两组资料比较时,也可用计算法。用计算法时,对两组数据各自排队、统一编秩号同查表法,不同的是求得秩号之和以后计算,公式是:
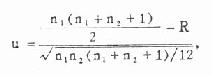 u0.05=1.96u0.01=2.58 (10.7)
u0.05=1.96u0.01=2.58 (10.7)
为便于计算和前后符号一致,n1作为较小样本例数,R 为较小样本的秩和,n2则为较大样本的例数。
本例 n 1=8,R=99,n2= 9 代入公式得:
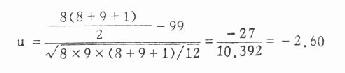
今∣u∣>u0.01, 故 P <0.01,在 α =0.01 水准上拒绝 H 接受 H 1,其结论同查表法,
据研究,当 n 1、n2都大于 8 时,算得的 u 近于正态分布,若例数太少,则以查表法更为精确。
本例如用 t 检验的团体比较处理,则 t =3.169,P<0.01,二者结论一致,但与符号检验结论不同(χ2=2.930,P>0.05)同样说明符号检验较粗糙,检验效率低,而秩和检验与 t 检验的结论较近。
三、两组等级资料的比较
等级资料又称为半计量资料,当两组等级资料比较时,用秩和检验来比较其相差是否显着比用 χ 2检验要恰当。两组等级资料,通常例数都较多,故一般都用计算法,其步骤与两组资料的秩和检验相似,不同的是要求各等级的平均秩号,为此,先要求得各等级的秩号范围。今举例 10.5 说明之。
1.求各等级的平均秩号。为此,先要求出各等级的秩号范围,如等级“-”共 18+8=26 例,共秩号范围自 1~26。要注意的是各等级的秩号范围必须紧相联接。最后一组秩号范围的上限一定等于两组例数之和。求得各等级秩号范围后,再求其下限和上限的平均,即可算得平均秩号,如等级“一”的平均秩号为(1+26)/2=13.5。余类推。
2.求出 R 及其 n 1,为计算方便,把例数少的正常人组的秩号之和作为 R 其例数为 n 1得 R =308,n1=20,n1=32
3.代入式(10.7)得 u 值,即可作结论。
例 10.5,今有 20 名正常人和 32 名铅作业工人尿棕色素定性检查结果如下表 10.5,试问其相差是否显著?
表 10.5 20 名正常人和 32 名铅作业工人尿棕色素定性检查结果
| 尿棕色素定性结果 | 正常人 | 铅作业工人 | 合计 | 秩号范围 | 平均秩号 | 例数较小组的秩和 |
| – | 18 | 8 | 26 | 1—26 | 13.5 | 243 |
| + | 2 | 10 | 12 | 27—38 | 32.5 | 65 |
| ++ | — | 7 | 7 | 39—45 | 42.0 | — |
| +++ | — | 3 | 3 | 46—48 | 47.0 | — |
| ++++ | — | 4 | 4 | 49—52 | 50.5 | — |
n1=20 n2=32 R=308
代入式(10.7)
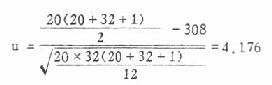
u0.01=2.58,今 u >u0.01,故 P <0.01,在 α =0.01 水准上拒绝 H,接受 H 1。两组相差显著,铅作业工人尿棕色素比正常人为高。
四、多组资料的比较
多组资料的比较也是从排秩号开始,但不是直接用秩和进行检验,有的书籍称之为秩检验(rank test),以示与秩和检验有别,其检验假设也较复杂:在处理完全随机设计的资料时,H:F(X1)=F(X2)=F(X3)=……,即比较的各样本所对应的各总体的分布函数相等,H1:各总体的分布函数不相等或不全相等;在处理随机单位组设计的资料时,H:P(χij=r)=1/n,即内组各秩号 r 之概率相等,都是 1 /n(r=1,2,……,n)而 H 1为:P=(χij=r)≠1/n。
因不同实验设计所得资料的处理也有别,故下面分别举例说明之。
(一)完全随机设计所得资料的比较
用的方法是单因素多组秩检验,称为 Kruskal-Wallis 氏法,或 H 检验。其计算步骤如下。
1. 各自排队,统一编秩号。即将各组数据在本组内从小到大排队,见表 10.6 各含量栏,再将各组数值一起考虑编出统一秩号,见表 10.6 各“秩号”栏,分属不同组的相同数值用平均秩号;
2. 求各组秩号之和 R 1以及各组数 n 1:
3. 代入下式计算 H 值:
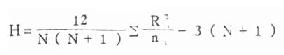 (10.8)
(10.8)
式中 N 为各组例数之和,Ri 和 ni 为各组的秩号之和以及例数:
4.查表作结论
当比较的组数多于三组,或组数虽只有三组但每组例数大于 5 时,H 值的分布近于自由度等于组数 - 1 的 χ 2分布,故可用对应的 χ 2值作界值。当三组比较时每组例数均不超过 5 时,H 值与 χ 2值有较大偏离,此时可查附表 14,直接查得 H 0.05和 H 0.01。
例 10.6 雄鼠 20 只随机分为四组,第 1、2 组在皮肤上涂用放射性锡(Sn113)标记的三乙基硫酸锡,涂后将皮肤暴露于空气中;第 3、4 组涂药后用密闭小玻璃管套使皮肤与外界空气隔开,三小时后杀死,测肝中放射物,结果如表 10.6,试比较各组含量间有无显著相差?
表 10.6 白鼠皮肤涂药后,肝中放射性 S n113的含量
| 涂干药后敞开 | 涂湿药后敞开 | 涂干药后密闭 | 涂湿药后密闭 | ||||
| 含量 | 秩号 | 含量 | 秩号 | 含量 | 秩号 | 含量 | 秩号 |
| 0.00 | 1 | 1.82 | 11 | 0.66 | 5 | 3.67 | 14 |
| 0.42 | 2.5 | 2.79 | 12 | 0.71 | 6 | 4.46 | 16 |
| 0.42 | 2.5 | 3.07 | 13 | 0.75 | 7 | 4.51 | 18 |
| 0.59 | 4 | 4.19 | 15 | 0.83 | 8 | 5.07 | 19 |
| 0.97 | 9 | 4.47 | 17 | 1.49 | 10 | 6.02 | 20 |
| Ri | R1=19 | R2=68 | R3=36 | R4=87 | |||
| ni | n1=5 | n2=5 | n3=5 | n4=5 | |||
各组资料各自排队,统一编秩号,以及求各组的秩号之和 R i和例数 n i见表 10.6
代入式(10.8)得
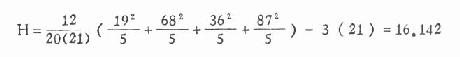
本例组数为 4(>3),查 χ 2值表,ν=4-1=3,得 χ 20.05,3=7.81,χ20.01,3=11.34,今 H >χ20.01,3,故 P <0.01,在 α =0.01 水准上拒绝 H,接受 H 1,即各组肝中放射性 Sn113含量差别显著。
(二)随机单位组设计所得资料的比较
用的方法是双因素多组秩检验,即 Friedman 氏法。
处理这种资料时可分成两步,对两个因素分别进行检验。现用例 10.7 说明其计算步骤:
先比较四种防护服对脉搏的影响
1.将穿四种防护服的每一受试者的脉搏数从小到大编秩号,当数值相等时用平均秩号,见表 10.7 各秩号栏。
2.求各防护服组秩号之和 Ri
3.代入式 10.9 求 H 值
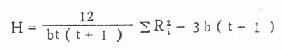 (10.9)
(10.9)
式中 t(treatment)为处理组数,b(block)为单位组数。
4.查表作结论
当 t >4 或 t = 4 且 b >5 或 t = 3 且 b >9 时,H 值的分布近于自由度 ν =t- 1 时的 χ 2分布,故可查相应的 χ 2值与 H 值比较作出判断:如 t、b 不能满足上述条件,则所算得的 H 值与 χ 2分布有较大偏离,需查附表 15 作判断。
例 10.7 受试者 5 人,每人穿四种不同的防护服时的脉搏数如表 10.7,问四种防护服对脉搏的影响有无显著差别?又五个受试者的脉搏数有无显著差别?
表 10.7 比较穿四种防护服时的脉搏数(次 / 分)
| 受试者 | 防护服 A | 防护服 B | 防护服 C | 防护服 D | ||||
| 编 号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 秩号 | 秩号 | 脉搏 | 秩号 |
| 1 | 144.4 | 4 | 143.0 | 3 | 133.4 | 1 | 142.8 | 2 |
| 2 | 116.2 | 2 | 119.2 | 4 | 118.0 | 3 | 110.8 | 1 |
| 3 | 105.8 | 1 | 114.8 | 3 | 113.2 | 2 | 115.8 | 4 |
| 4 | 98.0 | 1 | 120.0 | 3 | 104.0 | 2 | 132.8 | 4 |
| 5 | 103.8 | 2 | 110.6 | 4 | 109.8 | 3 | 100.6 | 1 |
| 秩秩号和 R i | 10 | 17 | 11 | 12 | ||||
t=4b=5
排队、编秩号、求各比较组的 R i见表 10.7 所示。
将表 10.7 中各数代入式 10.9,得
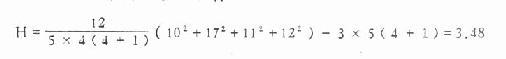
本例 t =4,b= 5 查附表 15,得 H 0.05=7.80,今 H >H0.05,故 P >0.05,在 α =0.05 水准上接受 H,无显著差别,故四种防护服对脉搏的影响无显著差别。
再比较五名受试者的脉搏数:
将数据列出(同表 10.7),但秩号是按每种防护服中受试者脉搏的数值从小到大编定,然后求出各受试者秩号之和 R 1,详细见表 10.8
表 10.8 比较五名受试者的脉搏数
| 受试者 | 防护服 A | 防护服 B | 防护服 C | 防护服 D | Ri | ||||
| 编 号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 脉搏 | 秩号 | 脉搏 | 秩号 | |
| 1 | 144.4 | 5 | 143.0 | 5 | 133.4 | 5 | 142.8 | 5 | 20 |
| 2 | 116.2 | 4 | 119.2 | 3 | 118.0 | 4 | 110.8 | 2 | 13 |
| 3 | 105.8 | 3 | 114.8 | 2 | 113.2 | 3 | 115.8 | 3 | 11 |
| 4 | 98.0 | 1 | 120.0 | 4 | 104.0 | 1 | 132.8 | 4 | 10 |
| 5 | 103.8 | 2 | 110.6 | 1 | 109.8 | 2 | 100.6 | 1 | 6 |
t=5b=4
将表 10.8 所得各数据代入式 10.9 得
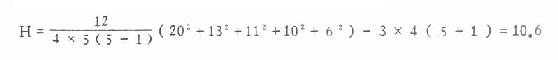
此处 t >4, 故查 ν =5-1= 4 时的 χ 2值表,得:χ20.05,4=9.49,χ20.01,4=13.28,今 χ 20.05,4<h<x20.01,4,故 0.05>P>0.01,在 α =0.05 水准上拒绝 H,接受 H 1,差别显著;即五名受试者脉搏数相差显著,1 号受试者最高,5 号受试者最低。</h<x
五、多组资料间的两两比较
当多组间的差别显着时,则需进一步判断那些组之间的差别有显着性,这个问题的解决方法与第八章第二节中的多个均数间的两两比较很相似,在例 10.6 四个实验组涂放射性锡的例子中,结果为 H >χ20.01,3,P<0.01,现以此为例,进一步作各组两两间比较,步骤如下:
1.将各组秩和从大到小依次排队,并求得两两间的相差,见表 10.9
2.计算标准误,计算公式是:
![]() (10.10)
(10.10)
式中 σ 为任意两个秩和之差的标准误,n 为各组例数,a 为处理数,此式要求各组例数相等,
3.查 q 值表定界限作结论
仍查方差分析时用的 q 值表,v→∝
各 q 值须与处理数相同的标准误相乘,如处理数为 2 的 q 值要乘以处理数为 2 时的标准误,2.77×6.77=18.75,3.64×6.77=24.64 等,余类推。
例 10.6 资料两两间比较如下:
表 10.9 每两组秩和之间的相差及其显著性
| 组别 | 秩和 R i | Ri—19 | Ri—36 | Ri—68 |
| 涂湿药后密闭 | 87 | 68** | 51** | 19* |
| 涂湿药后敞开 | 68 | 49** | 32** | |
| 涂干药后密闭 | 36 | 17 | ||
| 涂干药后敞开 | 19 |
计算标准误:n=5,用式 10.10
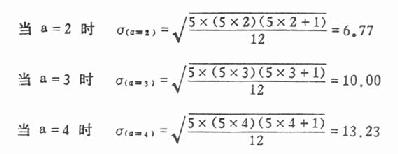
查 q 值表,得:
| 处理数 | 2 | 3 | 4 |
| q0.05,∞ | 2.77 | 3.31 | 3.63 |
| q0.01,∞ | 3.64 | 4.12 | 4.40 |
| q0.05,∞σ | 18.75 | 33.10 | 48.02 |
| q0.01,∞σ | 24.64 | 41.20 | 58.21 |
两两比较后的结论见表 10.9 所示,结合起来看,结论是:涂湿药的比涂干药肝中放射性 Sn113含量要高,涂湿药中,密闭的比敞开的含量高。
第四节 秩相关
参数法中介绍的直线相关只适用于正态双变量资料,但实际资料有时不能满足这些条件。如两事物有相关,但其观测结果不是计量资料而是等级资料,此时即可用秩相关来表达和分析。
本节介绍常用的 Spearman 秩相关。今以例 10.8 介绍其一般计算步骤:
1.将资料列成便于计算用的表,见表 10.10,为便于编秩号,在列表时可按资料中一个变量的原始数据由小到大排队,但另一变量中各相应数值必须随成对关系变动,不能打乱。
2.两变量各自从小到大编秩号,同一变量数值相等时求平均秩号,见表 10.10 中的“秩号”栏。
3.求各对变量值秩号之差数 d,再求∑d2。
4.代入式 10.11,计算秩相关系数 r a(又称 Spearman 秩相关系数)
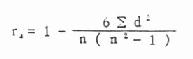 (10.11)
(10.11)
式中 n 为变量值的对子数。算得的 r 8与直线相关系数的意义相同,其范围在 -1~+ 1 之间,也分为正相关和负相关。
5.查表作结论
当 n >50 时,秩相关系数显著性的界值与直线相关系数相近似,故可根据 ν =n- 2 查附表 11 来作判断:当 n≤50 时,则查阅附表 16。
例 10.8 通过普查得到七个地区居民中单纯性甲状腺肿患者百分比与当地食物、水中的含磺量如表 10.10 右侧第一、第三两栏所列。问该两事物是否显著相关?
表 10.10 单纯性甲状腺肿患者百分数
与当地食物水中含碘量的秩相关分析
| 含 碘 量 | 患者百分数 | 秩号差 d | d2 | ||
| X1 | 秩号 | X2 | 秩号 | ||
| 71 | 1 | 16.9 | 7 | -6 | 36 |
| 81 | 2 | 4.4 | 6 | -4 | 16 |
| 126 | 3 | 2.5 | 5 | -2 | 4 |
| 154 | 4 | 0.8 | 3 | 1 | 1 |
| 155 | 5 | 1.1 | 4 | 1 | 1 |
| 178 | 6 | 0.6 | 2 | 4 | 16 |
| 201 | 7 | 0.2 | 1 | 6 | 36 |
n=7∑d2=110
将 n,∑d2代入式 10.11 得:
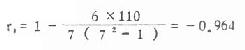
本例 n =7, 查例表 16,得 r 80.05,7=0.786,r8 0.01,7=0.929, 今∣r8∣>r80.01,7故 P <0.01,α=0.01 水准上拒绝 H,接受 H 1,故某地居民单纯性甲状腺肿患者百分数与当地食物、水中含碘量之间呈显著的负相关。
第五节 参照单位分析
参照单位分析适用于等级资料,如按疗效分为治愈、好转、无效、恶化,按反应分为 -、+、++、+++,和按麻醉效果分为Ⅰ、Ⅱ、Ⅲ、Ⅳ级等的资料。
参照单位分析又称 Ridit 分析,常是将等级资料中例数较多的一组的分布作为一个特定的分布来计算各等级的参照单位值(R 值),再参照这些 R 值计算各组的加权平均 R 值并进行假设检验。Ridit 的前三个字母是 Relative to an indentifieddistribution 的缩写,-it 是 unit 的字尾,故其含义是“相对于某一特定分布的单位”。由于有时将 idantifieddistribution 称为 reference distribution,故译为参照单位。
参照单位分析一般计算步骤如下:
1.选标准组
标准组的选择可根据各组例数多少以及所研究的问题而定。一般选例数多的组为标准组。如果各组例数相近或都较少时,可用合计数为标准组,(但若各组例数过少,则不宜用此法,可用秩和检验);若研究的是新、旧药物的疗效,则可以旧药为标准组;若研究的是患者与正常人相比较,则可选正常人为标准组。另外,标准组中的数字要求分布于各个等级,如果有的等级为 0 或过于少,将对计算结果产生影响。本例选辩中西组为标准组。
2.计算标准组的参照单位值,(R 值)
计算前最好将各等级按由弱到强的次序排列。计算的步骤与方法是:①计算标准组各等级的 1 / 2 值②求标准组累计例数并下移一行③将①、②求得的值按各等级相加④以标准组总例数除之,即得标准组各等级的 R 值。
3.参照标准组的 R 值,计算各组的平均 R 值(r)
将每组中各不同疗效者例数与标准组对应的 R 值相乘,将乘积加总,再除以该组总例数,即为 R,公式为
![]() (10.12)
(10.12)
4.计算各组的 95% 可信区间进行显著性检验,R 值的标准差为![]() ,故 R 值的标准误为
,故 R 值的标准误为
![]() (10.13)
(10.13)
R 的 95% 可信限为
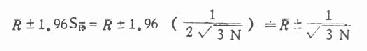
(10.14)
按此公式算得各组的 95% 可信区间后,作两两间的比较,凡无重叠者即有显著差别;有重叠者则无显著差别。
例 10.9 四种疗法治疗溃疡病的疗效如表 10.11,试比较其疗效。
表 10.11 几种疗法治疗溃疡病的疗效
| 疗效 | 例 数 | 百分比(%) | ||||||
| 西组 | 中组 | 辩中组 | 辩中西组 | 西组 | 中组 | 辩中组 | 辩中西组 | |
| 治愈 | 15 | 10 | 16 | 214 | 41.7 | 18.5 | 40.0 | 61.1 |
| 显效 | 8 | 11 | 13 | 93 | 22.2 | 20.4 | 32.5 | 26.6 |
| 好转 | 9 | 20 | 9 | 39 | 25.0 | 37.0 | 22.5 | 11.2 |
| 无效 | 4 | 13 | 2 | 4 | 11.1 | 24.1 | 5.0 | 1.1 |
| 合计 | 36 | 54 | 40 | 350 | 100.0 | 100.0 | 100.0 | 100.0 |
注:西组为单纯西药组,中组为单纯中药组,辩中组为辩证分型中草药组,辩中西组为辩证分型中西医结合组。
选辩中西组为标准组,并计算其 R 值如表 10.12
表 10.12 标准组 R 值计算表
| 疗效 | 例数 (1) | (1)/2 (2) | 累计例数并下移一行(3) | (2)+(3)(4) | R 值(4)/n(5) |
| 无效 | 4 | 2.0 | 2.0 | 0.006 | |
| 好转 | 39 | 19.5 | 4 | 23.5 | 0.067 |
| 显效 | 93 | 46.5 | 43 | 89.5 | 0.256 |
| 治愈 | 214 | 107.0 | 136 | 243.0 | 0.694 |
N=350
R 值的计算,也可用百分比进行,结果相同,见表 10.13
表 10.13 用百分比求 R 值的计算表
| 疗效 | 百分比 (1) | (1)/2 (2) | 累计例数并下移一行(3) | (2)+(3) (4) | R 值(4)/n (5) |
| 无效 | 1.1 | 0.55 | 0.55 | 0.006 | |
| 好转 | 11.2 | 5.60 | 1.1 | 6.70 | 0.067 |
| 显效 | 26.6 | 13.30 | 12.3 | 25.60 | 0.256 |
| 治愈 | 61.6 | 30.55 | 38.9 | 69.45 | 0.695 |
N=100.0
再计算各组的 R 值(加权平均参照单位值),用式(10.12),式中各符号结合本例含义是
式中∑为总和,f 为各不同疗效者例数,R 为与 f 同一疗效之标准组的 R 值。
标准组的 R 值应为 0.5,可用以核对 R 值是否算对。
本题各组 R 计算如下:
R 辩中西 =(4×0.006+39×0.067+93×0.256+2.4×0.694)/350=0.500
R 西 =(4×0.006+9×0.067+8×0.256+15×0.694)/36=0.363
R 中 =(13×0.006+20×0.067+11×0.256+10×0.694)/54=0.207
R 辩中 =(2×0.006+9×0.067+13×0.256+16×0.694)/40=0.376
将各组 R 值与例数代入式 10.14,得各组 95% 可信限如下:
辩中西
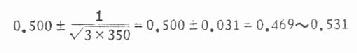
西组
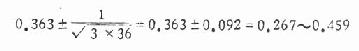
中组

辩中组
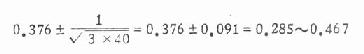
将各组的 95% 可信区间图示如下:
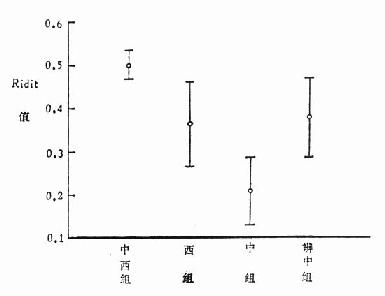
图 10.1 四种疗法治疗溃疡病疗效的比较(Ridit 分析)
根据以上四个区间及其示意图可以看出,辩中西组的区间与其它三组都不重叠,其它三组中西组和辩中组两区间有较大重叠,而与中组都是稍有重叠,在这种情况下可作较精确的分析,因为上述 R 值的标准差为![]() ,或方差为 1 /12,只是一个近似值,据数理统计研究,R 值的方差是一个逐渐接近 1 /12 并以 1 /12 为最大值。它与等级数有关,随着等级的增多,最大方差愈来愈接近 1 /12。表 10.14 是资料的等级数与最大方差。
,或方差为 1 /12,只是一个近似值,据数理统计研究,R 值的方差是一个逐渐接近 1 /12 并以 1 /12 为最大值。它与等级数有关,随着等级的增多,最大方差愈来愈接近 1 /12。表 10.14 是资料的等级数与最大方差。
表 10.14 各种等级数时的最大方差
| 等级数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 最大方差 | 1/16 | 2/27 | 5/64 | 2/25 | 30/432 | 4/49 | 21/256 | 20/243 |
实际资料的方差都小于 1 /12,故用以推算得的可信区间偏大,假设检验结论比较保守。本例中组与辩中组的区间重叠部分甚少,用表 10.14 内数值代替 1 /12,则可得到更为适当的结果。该资料等级数为 4,查表 10.14 得最大方差为 5 /64 故标准误为![]() ,以此计算西组、中组、辩中组的 95% 可信区间如下:
,以此计算西组、中组、辩中组的 95% 可信区间如下:
西组
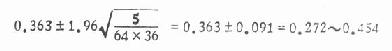
中组
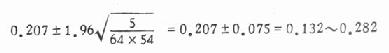
辩中组
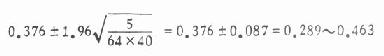
这样就可以认为中组与辩中组疗效相差也是显著的,虽然这里用的仍是最大方差,但是等级为 4 时的最大方差,假设检验结论还是比较保守的,但比用 1 /12 要精确些,当等级小于 4 时,更以查此表数值为宜。
练习题
1.试用符号与成对资料的秩和,检验两组鼠肝中维生素 A 含量(国际单位 / 克)有无显着差异,并与 t 检验的结果作比较。
不同饲料组鼠肝维生素 A 含量
| 大鼠配偶组 | 肝中维生素 A 含量 | 差数 d | |
| 正常饲料组 | 维生素 E 缺乏组 | ||
| 1 | 3550 | 2450 | 1100 |
| 2 | 2000 | 2400 | -400 |
| 3 | 3000 | 1800 | 1200 |
| 4 | 3950 | 3200 | 750 |
| 5 | 3800 | 3250 | 550 |
| 6 | 3750 | 2700 | 1050 |
| 7 | 3450 | 2500 | 950 |
| 8 | 3050 | 1750 | 1300 |
2.试用符号及两组资料的秩和,检验某地克山病患者 10 人与健康者 13 人的血磷含量(mg%)有无显著差别,并与 t 检验的结果作比较。
急性克山病患者与克山病区健康人血磷 (mg%) 测定值比较
| 患者 | 2.60 | 3.24 | 3.73 | 3.73 | 4.32 | 5.18 | 5.58 | 5.78 | 6.40 | 6.53 | |||
| 健康人 | 1.67 | 1.98 | 1.98 | 2.33 | 2.34 | 2.50 | 3.60 | 3.73 | 4.14 | 4.17 | 4.57 | 4.82 | 5.78 |
3.在研究人参镇镇静作用的实验中,曾有人以 5% 人参浸液对某批小白鼠 20 只作腹腔注射,而以等量蒸馏水对同批 12 只小白鼠作同样注射为对照,问能否说人参有显著的镇静作用?
人参镇静作用的实验结果
| 镇静等级 | 例 数 | |
| 人参组 | 对照组 | |
| – | 4 | 11 |
| ± | 1 | … |
| + | 2 | 1 |
| ++ | 1 | … |
| +++ | 12 | … |
4.试用秩和检验健康人和各期矽肺病人的血清粘蛋白含量(毫克 /100 毫升)间有无显著差异。
健康人与各期矽肺病人的血清粘蛋白含量(毫克 /100 毫升)
| 正常人 | 0—I 期矽肺 | I 期矽肺 | Ⅱ期矽肺 | Ⅲ期矽肺 |
| 64.26 | 62.01 | 65.45 | 74.97 | 77.11 |
| 42.84 | 67.33 | 69.63 | 88.06 | 82.58 |
| 52.48 | 70.40 | 69.73 | 93.47 | 83.53 |
| 48.19 | 78.91 | 74.97 | 95.10 | 89.01 |
| 80.22 | 85.68 | 80.44 | 100.67 | 97.58 |
| 69.61 | 85.68 | 80.44 | 101.14 | 103.81 |
| 48.19 | 91.15 | 95.20 | 113.52 | 107.10 |
| 58.90 | 94.82 | 96.39 | 118.98 | 178.42 |
5.12 名 2 - 7 岁急性白血病患儿的血小板及其出血状况的资料如下表,根据这一资料能否判断血小板数目与出血严重程度之间有显著相关?
12 名急性白血病患儿的血小板出血状况
| 血小板 | 出血状况 |
| 12,160 | 明显 |
| 13,790 | 较明显 |
| 16,500 | 个别出血点 |
| 31,050 | 无 |
| 42,600 | 较明显 |
| 34,270 | 较明显 |
| 74,240 | 无 |
| 106,430 | 无 |
| 126,170 | 无 |
| 129,000 | 无 |
| 143,880 | 明显 |
| 200,400 | 无 |
6.试比较下表中三种复方小叶枇杷对老年性慢性支气管炎治疗的效果。
三种复方小叶批杷对老年性慢性支气管炎疗效的比较
| 疗效 | 例 数 | 百分比(%) | ||||
| 老复方 | 复方 I | 复方Ⅱ | 老复方 | 复方 I | 复方Ⅱ | |
| 近控 | 36 | 4 | 1 | 9.4 | 4.0 | 2.6 |
| 显效 | 115 | 18 | 9 | 30.1 | 17.8 | 23.1 |
| 好转 | 184 | 44 | 25 | 48.2 | 43.6 | 64.1 |
| 无效 | 47 | 35 | 4 | 12.3 | 34.6 | 10.2 |
| 合计 | 382 | 101 | 39 | 100.0 | 100.0 | 100.0 |
第十一章 实验设计
第一节 实验设计的意义、原则与基本内容
一、实验设计的意义
实验设计是科学研究计划内关于研究方法与步骤的一项内容。在医学科研工作中,无论实验室研究、临床疗效观察或现场调查,在制订研究计划时,都应根据实验的目的和条例,结合统计学的要求,针对实验的全过程,认真考虑实验设计问题。一个周密而完善的实验设计,能合理地安排各种实验因素,严格地控制实验误差,从而用较少的人力、物力和时间,最大限度地获得丰富而可靠的资料。反之,如果实验设计存在着缺点,就可能造成不应有的浪费,且足以减损研究结果的价值。总之,实验设计是实验过程的依据,是实验数据处理的前提,也是提高科研成果质量的一个重要保证。
二、实验设计的原则
实验设计有属于专业方面的,有属于统计方面的。从统计方面说,主要应当考虑对照、重复、随机化等问题,这就是所谓实验设计的三原则。其具体内容我们将在第二、三、四节介绍。
三、实验设计的基本内容
(一)拟定相互比较的处理 所谓处理,指的是在实验研究中欲施加给受试对象的某些因素。如营养实验的各种饲料,治疗某病的几种疗法或药物,药理研究中某药的各种剂量等。在实验的全过程中,处理因素要始终如一保持不变,按一个标准进行实验。如果实验的处理因素是药物,那么药物的成份、含量、出厂批号等必须保持不变。如果实验的处理因素是手术,那么就不能开始时不熟练,而应该在实验之前使熟练程度稳定一致。
(二)确定实验对象及数量 这里指的是实验所用的动物或活体组织标本等。在实验设计中,要根据实验观察的目的与内容,明确规定采用什么样的实验对象,实验对象中的每个实验单位必须具备的条件与要求,以保证受试对象的一致性。实验对象需要有一定的数量,例数不能太少,也不宜过多。如何估计例数,详见第四节。
(三)确定将各实验单位分配到各种处理中去的原则 这主要是随机分配或随机化问题。第三节将介绍几种常用的随机分组方法。
(四)拟定观察项目和登记表 要根据研究目的和任务,选择对说明实验结论最有意义,并具有一定特异性、灵敏性、客观性的观察项目。必要的项目不可遗漏,数据资料应当完整无缺;而无关紧要的项目就不必设立,以免耗费人力物力,拖延整个实验的时间,尔后,要按照观察项目之间的逻辑关系与顺序,编制成便于填写和统计的登记表,以便随时记录实验过程中获得的数据资料。同一项目的度量衡单位必须统一符号(如 +、++、+++ 等),应有明确的定义。
(五)拟定对资料整理分析的预案 这就是对将获得的数据资料准备如何进行整理?要计算哪些统计指标?用什么统计分析方法?事先必须有个初步的设想。例如对计数资料,是计算率还是百分比?若计算率,分子是什么?分母是什么?各组同一项目的某个率或百分比如何进行比较?又如对计量资料,是计算算术均数、几何均数还是中位数?同一项目各均数间应采用什么方法作比较?切忌实验设计时不认真考虑,实验过后拿数字去找统计方法。
第三节 常用的随机化方法
一、随机化的重要性
随机化是指每个受试单位以概率均等的原则,随机地分配到实验组与对照组。例如将 30 只动物等分为 3 组,对其中每只动物来说,分到甲组、乙组、丙组的概率都应是三分之一。如果违背随机的原则,不论是有意或无意的,都会人为地夸大或缩小组与组之间的差别,给实验结果带来偏性。例如在营养学研究中,有的以实验动物体重增加情况作为饲料营养价值高低的标志。但体重的增加还同动物健康状况、食量大小等因素有密切关系。如果在实验研究之前,实验者希望某组获得较理想的结果,于是将那些雄性的、健康状况最佳的、食量最大的动物都分到该组,这就是有意夸大了组间差别,必须造成实验结果虚假和不稳定。为了避免此类偏性,随机化就是一个重要手段。如本例,要求分配到各组的动物必须性别相同,体重相近,健康状况相似。总之要使各处理组非实验因素的条件均衡一致,以抵消这些非实验因素对实验结果的影响。强调实验设计要遵守随机化原则,还有一个理由,就是只有合乎随机原则的资料才能正确应用数理统计上的各种分析方法,因为数理统计各种理论公式都是建立在随机化原则基础上的。那些事先加入主观因素,以致不同程度失真的资料,统计方法是不能弥补其先天不足的,得出的结论也必然是错误的。
二、随机分组举例
数理统计学家根据概率论的原理编制了随机数字表 (附表 17) 与随机化分组表(附表 18),它们都是科研工作中用于随机化的工具表。现举例说明其用法,并介绍几种简单而常用的实验设计。
(一)配对设计 配对设计是将受试对象按某些特征或条件配成对子,然后分别把每对中的两个受试对象随机分配到实验组与对照组(或不同处理组)。这种设计的优点是能缩小受试对象间的个体差异,从而减少实验误差,提高实验效率。受试对象配对的特征或条件,主要是指年龄、性别、体重、环境条件等非实验因素,不要以实验因素作为配对条件。如在动物实验中,常把窝别或性别相同、原始体重相近的两头动物配成对子;在人群试验中,有时把性别相同、年龄相近、生活或工作条件相似的两人配成对子。
在某些医学实验中,常就同一受试对象作比较,称为同体比较或自身对照,例如同一组病人用某药治疗前后某项指标的比较,同一批受试对象施加某种处理因素后不同部位或不同器官变化情况的比较,同一批检品施以不同检测方法或培养方法所得结果的比较,等等。从统计方法上说,这也属于配对实验。
采用配对设计时,实验者在整个实验过程中,必须始终能辩认属于同一对子的是哪两头动物,因此动物编号是非常重要的。记录实验数据应保持每对的一一对应关系,不能错乱或缺失。否则,就失去配对设计的意义了。
例 11.1 设有动物 20 头,要求按配对设计分为甲、乙两组。
先将同性别、同体重 (或体重非常接近) 的两头动物配成一个对子,共配成 10 对,并依次编为 (1)-(10) 号,然后从附表 17“随机数字表”的任何一页、任何一处开始,依一定方向抄下 10 个数字,依次排在配对号下。本例由附表 17 第 (1) 页第六横行第一个数字起向右抄录 10 个数字。凡随机数字为单数者,该对子中的第一头动物分入甲组,而同对子中的另一头动物则归入乙组;若随机数字为双数,就把该对子中的第一头动物分入乙组,而同对子中的另一头动物则归入甲组。于是本例分配结果如下:
| 配对号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| 随机数字 | 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 |
| 第一头动物组别 | 乙 | 乙 | 甲 | 乙 | 甲 | 甲 | 乙 | 甲 | 乙 | 乙 |
| 第二头动物组别 | 甲 | 甲 | 乙 | 甲 | 乙 | 乙 | 甲 | 乙 | 甲 | 甲 |
配对设计使用附表 18“随机化分组表”也是很方便的。若对子数在 10 对以内,可使用该表第 (1) 页,不足 10 对,例如只有 8 对,则弃去其中大于 8 的数字;若为 11—20 对,可使用该表第 (2) 页,不足 20 对,例如只有 15 对,则将其中大于 15 的数字舍弃;余类推。上例配成对子后,从该表第 (1) 页的任意一方抄录任意一个纵行或横行的 10 个数字,依次排列在配对号下,仍按上述分组方法确定每对动物的组别。
(二)完全随机设计 完全随机设计是将实验对象完全随机地分配到实验组与对照组或几个对比组中去,其设计和统计处理都比较简单,但实验效率较低。按实验的内容和要求。各组例数可相等或不等。
例 11.2 设有同性别、体重在一定范围内的健康动物 20 头,试用完全随机方法等分为甲、乙两组。
先将动物按原始体重由小至大依次编为 (1) 至(20)号,然后从随机数字表上抄录随机数字。假定本例自第 (2) 页第五纵行第一个数字起,向下抄 20 个数字。令随机数字的单数代表甲组,双数 (0 也作为双数) 代表乙组。结果分到甲组的只有 9 头动物,分到乙组的却有 11 头动物。因此乙组要调整一头动物到甲组去。调整动物组别,仍要用随机方法来决定。于是再向下抄录第 21 个数字是 21,用 11 除之,得余数为 10,我们把第十个“乙”改为“甲”,即把第 (19) 号动物调整到甲组,经过调整,两组动物数相等了。
| 动物编号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| 随机数字 | 67 | 54 | 46 | 69 | 26 | 69 | 82 | 89 | 15 | 87 |
| 组 别 | 甲 | 乙 | 乙 | 甲 | 乙 | 甲 | 乙 | 甲 | 甲 | 甲 |
| 调整组别 | ||||||||||
| 动物编号 | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) |
| 随机数字 | 46 | 59 | 22 | 40 | 66 | 35 | 84 | 57 | 54 | 30 |
| 组 别 | 乙 | 甲 | 乙 | 乙 | 乙 | 甲 | 乙 | 甲 | 乙 | 乙 |
| 调整组别 | 甲 |
从上面的例子可以看到,随机数字虽属随机,但有的数字均匀性不够理想,以致分得的各组例数常不相等,不得不进行调整,增加了使用时的困难。若用附表 18 随机化分组表则较简便。仍如上例,因共有 20 头动物,所以应使用该表第 (2) 页。假定我们取其中第 2 组随机数字,仍令单数代表甲组,双数代表乙组,于是分配结果如下:
| 动物编号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| 随机数字 | 19 | 04 | 03 | 15 | 13 | 10 | 17 | 12 | 09 | 16 |
| 组别 | 甲 | 乙 | 甲 | 甲 | 甲 | 乙 | 甲 | 乙 | 甲 | 乙 |
| 动物编号 | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) |
| 随机数字 | 05 | 02 | 06 | 11 | 08 | 20 | 07 | 18 | 01 | 14 |
| 组别 | 甲 | 乙 | 乙 | 甲 | 乙 | 乙 | 甲 | 乙 | 甲 | 乙 |
例 11.3 设有同性别、体重在一定范围内的健康动物 18 头,要求等分为甲、乙、丙三组。
按前面的方法给动物编号。本例从附表 17(5)第十一横行与第二十纵行相交处的数字起,向左抄下 18 个数字。因为要分成三组,所以每个随机数目要用 3 来除 (若分四组即用 4 来除,余类推),并写下余数。如果被除数小于除数,商数为 0,那么被除数即为余数;如果被除数为 0,余数亦为 0。然后按余数分组:余数为 1,即将动物归入甲组;余数为 2,归入乙组;余数为 0,归入丙组(分四组时,余数为 3 归入丙组,余数为 0 归入丁组,余类推)。分组结果,甲、乙两组各有 5 头动物,而丙组有 8 头动物。要使三组动物相等,则须将丙组的两头动物调整给甲、乙组各一头。我们仍接着向左抄录两个数目,得 83、89。先用 8(因为丙组有 8 头动物) 去除 83,得余数为 3,于是把原分配的第三个“丙”即第 (6) 号动物改为“甲”;再用 7(因丙组还有 7 头动物)去除 89,得余数为 5,于是把剩余的第五个“丙”即第 (9) 号动物改为“乙”。这里要指出,调整组别时,如果随机数字被除尽,余数为 0,将调整哪一个?如本例,若除数是 8 就调整第八个“丙”,若除数是 7 就调整第七个“丙”,余类推。
| 动物组别 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| 随机数字 | 46 | 90 | 16 | 18 | 17 | 36 | 87 | 24 | 33 |
| 以 3 除后之余数 | 1 | 1 | 2 | ||||||
| 组 别 | 甲 | 丙 | 甲 | 丙 | 乙 | 丙 | 丙 | 丙 | 丙 |
| 调整组别 | 甲 | 乙 | |||||||
| 动物编号 | (10) | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) |
| 随机数字 | 56 | 97 | 59 | 47 | 96 | 97 | 80 | 69 | 40 |
| 以 3 除后之余数 | 2 | 1 | 2 | 2 | 1 | 2 | 1 | ||
| 组 别 | 乙 | 甲 | 乙 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 |
| 调整组别 |
本例若用表 18,仍应从第 (2) 页任取一组随机数字。假定取第 8 组,先舍去其中大于 18 的数字,然后以随机数目 01—06 分入甲组,07—12 分入乙组,13—18 分入丙组。结果如下:
| 动物编号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| 随机数字 | 17 | 14 | 09 | 15 | 05 | 13 | 02 | 08 | 18 |
| 组别 | 丙 | 丙 | 乙 | 丙 | 甲 | 丙 | 甲 | 乙 | 丙 |
| 动物编号 | (10) | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) |
| 随机数字 | 04 | 16 | 03 | 06 | 11 | 01 | 10 | 07 | 12 |
| 组别 | 甲 | 丙 | 甲 | 甲 | 乙 | 甲 | 乙 | 乙 | 乙 |
3.随机单位 (区) 组设计 这种设计实际上是配对设计的扩大。配对设计是将多方面条件近似的受试对象配成对子,而这种设计是将多方面条件相同或相近的受试对象组成单位组(亦称区组或配伍组)。每个随机单位组的受试对象数目取决于处理的数目。如果一个实验安排了四种不同处理,那么每个单位组就应有四个受试对象。有多少个单位组,则每种处理就可以分配到多少个受试对象。这种设计,各随机单位组的受试对象不仅数目相等,而且生物学特点也较均衡,缩小了组间差别,实验效率较高。
例 11.4 设有动物 24 头,要求按随机单位组设计分为四个处理组。
先将每四头性别、体重等条件近似的动物组成一个单位组,共得六个单位组。第一个单位组编为 (1) 至(4)号,第二个单位组编为 (5) 至(8)号,余类推。从附表 17 第 (6) 页第十纵行最下一个数字开始,向上抄写 18 个数字,每个单位组内填入三个数字、留一个空位。然后将同一单位组中的三个随机数字依次以 4、3、2 除之,再按余数确定前三个动物组别:如第一单位组中第一个余数是 1,在“甲乙丙丁”四字中列第一位者为“甲”,故将 (1) 号动物分入甲组;第二个余数是 2,这时在“乙丙丁”三字中列第二位者为“丙”,故将 (2) 号动物分入丙组;第三个余数是 0,这里在“乙丁”二字中“丁”列第末位,故将 (3) 号动物分入丁组。该单位组内剩下的 (4) 号动物不能随机分配,必须分入乙组。值得注意的仍然是在整个实验过程中,必须始终能辨认属于同一单位组的是哪几头动物。
| 动物编号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
| 随机数字 | 17 | 14 | 82 | — | 98 | 54 | 77 | — | 08 | 23 | 38 | — |
| 除数 | 4 | 3 | 2 | — | 4 | 3 | 2 | — | 4 | 3 | 2 | — |
| 余数 | 1 | 2 | — | 2 | 1 | — | 2 | — | ||||
| 组别 | 甲 | 丙 | 丁 | 乙 | 乙 | 丁 | 甲 | 丙 | 丁 | 乙 | 丙 | 甲 |
| 动物编号 | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | (22) | (23) | (24) |
| 随机数字 | 64 | 14 | 42 | — | 48 | 26 | 88 | — | 68 | 85 | 63 | — |
| 除数 | 4 | 3 | 2 | — | 4 | 3 | 2 | — | 4 | 3 | 2 | — |
| 余数 | 2 | — | 2 | — | 1 | 1 | — | |||||
| 组别 | 丁 | 乙 | 丙 | 甲 | 丁 | 乙 | 丙 | 甲 | 丁 | 甲 | 乙 | 丙 |
随机单位组设计亦可用附表 18,如本例,按上述方法给动物编号后,取第 (1) 页的任一方数字。若取第 2 方,我们从第一横行中摘数字 1—4,依次填入第一个单位组的各动物号下,舍去其它数字;再取第二横行中的 1 至 4 依次填入第二个单位组各动物号下;依次类推。随机数字即各动物所属处理组别。结果如下:
| 动物编号 | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
| 随机数字 | 3 | 2 | 4 | 1 | 2 | 3 | 1 | 4 | 4 | 1 | 3 | 2 |
| 组 别 | 丙 | 乙 | 丁 | 甲 | 乙 | 丙 | 甲 | 丁 | 丁 | 甲 | 丙 | 乙 |
| 动物编号 | (13) | (14) | (15) | (16) | (17) | (18) | (19) | (20) | (21) | (22) | (23) | (24) |
| 随机数字 | 1 | 3 | 4 | 2 | 2 | 4 | 3 | 1 | 4 | 2 | 3 | 1 |
| 组 别 | 甲 | 丙 | 丁 | 乙 | 乙 | 丁 | 丙 | 甲 | 丁 | 乙 | 丙 | 甲 |
第三节 样本含量的估计
一、估计样本含量的意义及条件
我们在第一节里曾提到重复的原则。所谓重复,是指各处理组(对照在实验研究中也被看作是一种处理,而且是必不可少的)的受试对象都应有一定的数量,例数不能太少,所以在抽样调查、临床观察或实验研究中,首先总要考虑样本含量(或叫样本大小)问题。样本太小,使应有的差别不能显示出来,难以获得正确的研究结果,结论也缺乏充分的依据;但样本太大,会增加实际工作中的困难,对实验条件的严格控制也不易做到,并且造成不必要的浪费。所以这里所说的样本含量估计,系指在保证研究结论具有一定可靠性的条件下,确定最少的观察或实验例数。
但是,样本含量又是个比较复杂的问题。要讲清在各种情况下估计样本含量的方法和原理,那是很繁杂的。而且,不同的参考书上介绍的计算公式和工具表往往不一样,以致同一问题所得的结果也可能有出入。所以,不论按哪种公式或工具表求得的结果,也只能是个近似的估计数。
估计样本含量,必须事先明确一些条件与要求:
(一)根据研究目的与资料性质,要先知道一些数据。例如要比较几组计数资料,先要知道百分数或率;要比较几组计量资料,先要知道平均数及标准差。这些数据可从以往的实践,预备试验的结果、兄弟单位的经验或文献资料里得来。
(二)确定容许误差。由于抽样误差的影响,用样本指标估计总体指标常有一定的误差,因而要确定一个样本指标与总体指标相差所容许的限度。此值要求越小,所需例数就越多。
(三)确定把握度(1—β)。β 是第二型错误的概率;而 1—β 的意思是:如果两组确有差别,则在每 100 次实验中平均能发现出差别来的概率。把握度可用小数(或百分数)表示,一般取 0.99、0.95、0.90、0.80、0.50。要求把握度越高,则所需例数直多。
(四)确定显著性水平,即第一型错误的概率(α)。这就是希望在 α =0.05 的水准上发现差别,还是希望在 α =0.01 的水准上发现差别。α 越少,所需例数越多。
此外,估计样本含量时还应当根据专业知识确定用单侧检验或双侧检验。同一实验,若既可用单侧检验又可用双侧检验,则前者所需例数要少些。
二、用计算法估计样本含量
我们运用前面学过的某些假设检验公式,就可以进行样本含量的计算。下面仅举两例略作介绍。这里的公式仅适用于 α =0.05,1—β=0.50。而且都是双侧检验。
(一)两个率比较时样本含量的计算 令 n 为每组所需例数,P1、P2为已知的两个率(用小数表示),P 为合并的率,当设两组例数相等时,即 P =(P1+P2)/2。q=1=p,则
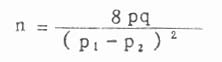 (11.1)
(11.1)
例 11.5 据某院初步观察,用甲、乙两种药物治疗慢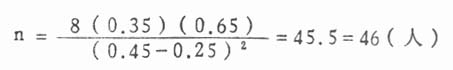 性气管炎患者,近控率甲药为 45%,乙药为 25%。现拟进一步试验,问每组需观察多少例,才可能在 α =0.05 的水准上发现两种疗法近控率有显著相差?
性气管炎患者,近控率甲药为 45%,乙药为 25%。现拟进一步试验,问每组需观察多少例,才可能在 α =0.05 的水准上发现两种疗法近控率有显著相差?
本例 P 1=0.45,P2=0.25,P=(0.45+0.25)÷2=0.25,q=1-0.35=0.65, 代入式 11.1
每组需观察 46 人,两组共观察 92 人,注意:例数问题不同于一般数学计算中的四舍五入,凡是有小数的值,应一律取稍大于它的正整数,如本例 45.5 取 46, 若为 45.1 也应取 46。
(二)个别比较 t 检验样本含量的计算 令 n 为所需样本数,S 为差数的标准差,X 为差数的均数,t0.05O为 t 值表上相当于 P =0.05 的 t 值,4 为 n 足够大时 t 20.05=1.962的数,则
大样本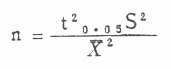 (11.2)
(11.2)
小样本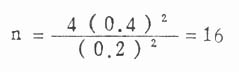 (11.3)
(11.3)
例 11.6 用某药治疗胃及十二指肠溃疡病人,服药四周后胃镜复查时,患者溃疡面平均缩小 0.2cm2,标准差为 0.4cm2,假定该药确能使溃疡面缩小或愈合,问需多少病人作疗效观察才能在 α =0.05 的水准上发出用药前后相差显著?
本例 X=0.2,S=0.4,先代入式(11.2)
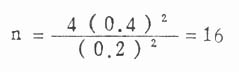
由于 n <30,故用式(11.3)重算。当 n=16,ν=16-1=15,t0.05=2.131,
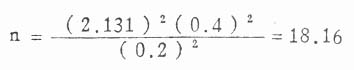
当 n=19(略大于 18.16),ν=19-1=18,t0.05=2.101
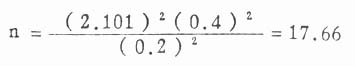
当 n=18,ν =18-1=17,t0.05=2.110
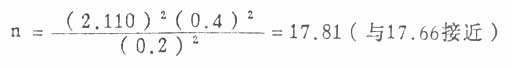
故至少需用 18 人作疗效观察。
三、用查表法估计样本含量
当要求平均有 80%、90% 以上的机会能发出相差显着或非常显着时,计算公式比较复杂,数理统计上已编制成工具表,一查便得,附表 19 只是其中的一部分。我们仍以前面的例题来介绍这些表的用法。
(一)两个率比较时所需样本含量 对于两个率的比较,单侧检验可查附表 19(1),双侧检验查附表 19(2)
仍用例 11.5 来说明。本例 P 1=45%,P2=25%,δ=45%-25%=20%,设 α =0.05,把握度为 0.80。如果已知甲药疗效不可能低于乙药,可用单侧检验,查附表 19(1)。我们从“较小率”栏中找到 25 横行,再从上方找到 δ =20 直行,基相交处,读上行数字得 69,即每组最少需要 69 例,两组共需 138 例。
如果两个率(或百分数)都超过 50%,怎样使用这个表呢?假定甲组阳性率是 80%,乙组阳性率是 65%,两组阳性率相差 15%。这时先求两组的阴性率,于是甲组阴性率为 20%,乙组阴性率为 35%,两组阴性率相差仍为 15%。若用双侧检验,我们查附表 19(2),从“较小率”栏找到 20 横行,再从上方找到 δ =15 直行,其相交处上行数字为 135,即每组需检查 135 例(两组共 270 例)将有 80% 的机会在 α =0.05 的水准上发现两组阳性率相差显著。
若表中查不到题中的“较小率”及 δ,可用最接近的值或内插法求 n,但宁可使 n 偏大,以免估计的样本含量偏少。
(二)个别比较 t 检验所需的样本含量 这是配对比较,应查附表 20。使用该表时,先要求出差数的总体均数 μ 与总体标准差 σ 之比,即 δ =μ/σ,当 μ 与 σ 未知时,可分别用 X 与 S 作为估计值。
仍用例 11.6 来说明,本例 X =0.2,S=0.40, 故 δ =μ/σ=0.2/0.4=0.5。若设 α =0.05,1—β=0.90, 用双侧检验,查附表得 20,得 n =44,即需观察 44 例病人。若设 α =0.05,1—β=0.50,则 n =18, 同计算法结果一致。
(三)两个均数比较所需样本含量 应查附表 21。先要求出两总体均数之差与总体标准差这比,即 δ =(μ1-μ2)/σ。若 μ 1及 μ 2未知时,可分别以 X 1及 X 2估计之;σ 未知时,可以合并标准差 S 估计之。
例 11.7 某职业病防治所用两种疗法治疗矽肺患者,一个疗程后,患者血清粘蛋白下降值甲疗法平均为 2.6(mg%), 乙疗法平均为 2.0(mg%,)两种疗法下降值之合并标准差为 1.3(mg%)。若发现两组疗效相差显著,每组至少应观察多少病人?
本例 X 1=2.6,X2=2.0,S=1.3, 故 δ =(μ1-μ2)/σ=(2.6-2.0)/1.3=0.46。若设 α =0.05,1—β=0.50,用双侧检验,查附表 21,δ=0.46 查不到。在这种情况下,可用邻近而略小的 δ 值代替,或用内插法估计。本例若查 δ =0.45,得 n =39,即每组需要 39 例,两组共需 78 例。若用内插法计算,当 δ =0.45 时所需例数是 39,δ=0.50 时所需例数是 32,所以 δ =0.46 时所需例数是:
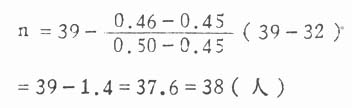
答案是:每组需要至少观察 38 例,两组共需观察 76 例。
[附] 资料的综合分析
前面几章介绍了常用的统计方法。在实验工作中,必须根据研究目的与资料性质,并结合专业知识,恰当地运用统计方法,才能做出正确的、符合实际的结论。例如:某院为探明胃液及胃组织的瘤胚抗原(Carcino embryonic Antigen CEA)在胃癌诊断、癌前病变筛选及随访方面的意义,胃液、胃组织 CEA 含量的相互关系,以及 CEA 与胃组织病理学改变的关系,测定了各种胃病患者的胃液、胃组织及血清中 CEA 含量,并用同样方法测定了部分正常人胃液 CEA 含量作为对照。表 1、表 2 是测量结果的一部分。下面我们简要介绍统计处理的一般程序及统计方法的选择。
表 1 三组不同人员胃液癌胚抗原(CEA)测定结果
| 组别 | 胃液 CEA 含量(ng/ml) | 定性结果 | ||||||
| 阳性 | 阴性 | |||||||
| 正常人组 | 20.4 | 30.2 | 210.4 | 365.0 | 56.8 | 37.8 | 2 | 30 |
| 265.3 | 175.0 | 169.8 | 256.4 | 254.0 | 262.3 | |||
| 170.5 | 360.0 | 78.4 | 86.4 | 128.0 | 24.1 | |||
| 28.5 | 108.5 | 472.5 | 158.6 | 238.7 | 253.6 | |||
| 57.0 | 189.6 | 59.3 | 259.3 | 380.2 | 210.5 | |||
| 64.6 | 87.3 | |||||||
| 萎缩性胃炎组 | 281.0 | 377.1 | 230.0 | 537.9 | 248.7 | 571.4 | 21 | 14 |
| 766.2 | 495.o | 87.3 | 389.8 | 423.9 | 577.3 | |||
| 66.8 | 521.3 | 327.8 | 421.4 | 149.7 | 47.5 | |||
| 425.7 | 270.8 | 378.5 | 228.0 | 538.4 | 245.6 | |||
| 584.1 | 648.8 | 485.6 | 110.8 | 398.7 | 452.6 | |||
| 587.7 | 86.8 | 532.1 | 311.6 | 442.2 | ||||
| 胃癌组 | 480.0 | 488.9 | 350.7 | 652.8 | 1400.0 | 850.0 | 24 | 4 |
| 725.6 | 590.0 | 765.0 | 1200.0 | 231.2 | 485.3 | |||
| 600.0 | 1380.0 | 438.5 | 652.4 | 432.8 | 296.1 | |||
| 608.8 | 688.5 | 630.5 | 750.0 | 815.0 | 664.0 | |||
| 348.6 | 550.0 | 640.0 | 464.8 | |||||
表 2 10 例胃癌患者胃液 CEA 含量与胃组织肿瘤 CEA 含量的关系
| 病例号 | 胃液 CEA 含量 | 胃组织肿瘤 CEA 含量 |
| (ng/ml) | (cm2·ng/mg) | |
| 1 | 432.8 | 6.6 |
| 2 | 488.9 | 8.2 |
| 3 | 600.0 | 15.7 |
| 4 | 608.4 | 14.8 |
| 5 | 640.2 | 16.2 |
| 6 | 750.0 | 15.8 |
| 7 | 815.0 | 18.2 |
| 8 | 1200.0 | 20.0 |
| 9 | 1380.0 | 20.0 |
| 10 | 1400.0 | 20.0 |
一、了解研究目的、资料搜集情况、数据意义、整理分析要解决什么问题
无论动物实验、临床观察或现场调查,应当目的明确,周密设计,精心操作,认真记录,务必使获得的原始资料完整、准确、真实、可靠。如果是替别人整理分析资料,在接受任务时,也首先必须把这些问题搞清楚,才能做出正确的、符合要求的分析。若发现某些资料不全或有可疑数值,应及时查明原因,加以改进,必要时补做实验或重新调查。本例研究目的已如上述。所观察的病人诊断都是明确的,标本采集,数据测定都是在实验室进行,仪器性能稳定,操作者技术熟练,资料是可靠的。统计分析的主要目的在于比较正常人、良性胃病患者、胃癌病人的胃液 CEA 含量有无显著差别,从而考虑该项指标能否作为胃癌早期诊断的一个辅助指标和随访的一个手段。此外,对胃液与胃组织肿瘤 CEA 含量作相关分析,找出它们间有无直线关系。
二、区分资料类型
这就是要分清所得到的资料哪部分是计量资料,哪部分是计数资料,尔后分别采用不同的统计分析方法来处理。本例表 1 左半部分是胃液中 CEA 含量,属计量资料;右半部分是以 95% 正常值范围单侧上限值 370(ng/ml)为界限,凡≥370(ng/ml)者为阳性,<370(ng/ml)者为阴性,然后清点每组阳性、阴性例数,这是计数资料。表 2 是对确诊的 10 例胃癌患者,既测定了胃液中 CEA 含量,又测定并计算出胃组织肿瘤 CEA 含量(根据前人经验用肿瘤面积与胃粘膜中 CEA 含量相乘,cm2·ng/ml)。显然,这是两个变量的问题。为方便叙述。我们按资料类型依次分析。
三、计量资料的处理
先要了解样本含量与频数分布情况。因为大样本或小样本、正态分布或偏态分布,统计方法的选择与统计指标的计算都有所不同。本例三组例数都在 30 左右,各组观察值分布比较均匀、对称,必要时可作正态性检验,故可按小样本、正态分布处理。
(一)计算平均数与标准差,以说明各观察值的集中趋势与变异情形。若观察值呈偏态分布,则应计算中位数;若系对数正态分布或等比资料,则计算几何均数。本例见表 3 第(3)第(4)栏。
(二)作为正常对照,用估计正常值范围的方法计算正常人组单侧上限 95% 正常值。宜用正态分布法;172.47+1.645×119.50=369.05,故以 370(ng/ml)作为单侧上限值。但由于例数较少,稳定性受到影响,因而还不能作为正常值范围来推广应用。
(三)计算标准误,以说明样本均数的散布情形,描述抽样误差的大小。必要时,用平均数与标准误结合,计算可信区间,以估计总体均数所在范围。见表 3 第(5)、第(6)栏。
表 3 各组平均数、标准差、标准误及 95% 可信区间
| 组别 | N | X | S | Sχ | 95% 可信区间 |
| (1) | (2) | (3) | (4) | (5) | (6) |
| 正常人组 | 32 | 172.47 | 119.50 | 21.12 | 129.38<μ<215.55 |
| 萎缩性胃炎组 | 35 | 378.52 | 182.33 | 30.82 | 315.89<μ<441.15 |
| 胃癌组 | 28 | 649.25 | 285.66 | 53.98 | 538.48<μ<760.02 |
(四)均数之间的比较:自身对照或配对设计资料(即成对计量资料)用个别比较 t 检验,两组均数比较用团体比较 t 检验,三组以上均数比较用方差分析。在方差分析前应作方差齐性检验,若方差不齐,则应用秩和检验,或经变量代换后再作方差分析。本例三组资料经代入式(8.5)与式(8.6)求得校正 χ 2值为 21.04,χ2>χ20.01,2,P<0.01,三组方差在 α =0.01 的水准上相差显著,故不宜用方差分析。所以我们用秩和检验,经代入式(10.8)得 H =50.321,H>χ20.01,2,P<0.01,在 α =0.01 的水准上相差显著。再用式(10.7)作两组之间的比较,结果正常人组与萎缩性胃炎组之间 u =4.475, 萎缩性胃炎组与胃癌组之间 u =4.150, 正常人组与胃癌组之间 u =6.253, 均在 α =0.01 的水准上相差显著,正常人组最低,萎缩性胃炎次之,胃癌组最高。
四、计数资料的处理
(一)计算有关的相对数,常用的是率与百分比。如本例,可求出三组的阳性率,见表 4。
表 4 三组胃液 CEA 阳性率(%)
| 组 别 | 检查例数 | 阳性例数 | 阴性例数 | 阳性率(%) |
| 正常人组 | 32 | 2 | 30 | 6.25 |
| 萎缩性胃炎组 | 35 | 21 | 14 | 60.00 |
| 胃 癌 组 | 28 | 24 | 4 | 85.71 |
| 合 计 | 95 | 47 | 48 | 49.47 |
(二)必要时,也可以计算率的标准误,以描述率的抽样误差大小;然后根据样本大小,分别用计算法或查表法求得率的可信区间,以估计总体率所在范围。
(三)几个率之间的比较,常用 χ 2检验。仅有两组的用四格表计算(当样本较大时也可用 u 检验),三组以上的用 2×K 表计算。本例共有三组,每组分为阳性、阴性两种类型,所以应用 2×K 表专用公式求 χ 2值。结果 χ 2=40.18,χ2>χ20.01,2,P<0.01,说明三组阳性率在 α =0.01 的水准上相差显著。再用四格表进行检验,结果正常人组与萎缩性胃炎组之间得 χ 2=19.10,χ2>χ20.01,1,P<0.01;正常人组与胃癌组之间得 χ 2=25.53,χ2>χ20.01,1,P<0.01。以上均在 α =0.01 的水准上相差显著,而萎缩性胃炎组与胃癌组之间得 χ 2=3.86,χ2>χ20.05,1,P<0.05,相差显著。我们在前面对三组胃液 CEA 含量用秩和检验作两两比较,结果都是在 α =0.01 的水准上相差显著,这说明计量资料获得信息多些。
五、两个变量间直线关系的分析
如果两变量的关系是相互的,分不清自变量与应变量,没有理由用一个变量去推算另一个变量,就只计算相关系数,不建立回归方程。如果两变量间存在直线关系,且需要从一个变量推算另一个变量时,可再建立回归方程,必要时还可以编制用一个变量估计另一个变量的对照表,本例 10 名胃癌患者胃液 CEA 含量与胃组织肿瘤 CEA 含量属于两个变量的关系问题,先计算相关系数,得 r =0.818,r>r0.01,8,P<0.01,在 α =0.01 的水准上相关显着。这说明肿瘤越大,胃组织病变越严重,胃液中 CEA 含量就越高,所以,若需要根据胃液中 CEA 含量推算病变严重程度,亦可计算回归方程。
根据以上统计分析,本例可得出如下结论:①胃癌病人的胃液 CEA 明显升高,提示可作为胃癌诊断的一个辅助指标,在早期胃癌诊断中可能有一定作用;其含量高低与肿瘤大小及胃组织 CEA 含量有关。②胃癌良性病变,胃液 CEA 含量也增高,提示该项指标可作为胃癌前疾病筛选和随访的一个手段。③良性病变与恶性病变胃液 CEA 含量重叠较多,所以应用该项指标作良性与恶性病变的鉴别诊断,尚待深入研究。
综合练习题
某院对城市入托与农村未入托儿童的智能及有关因素作了调查。现将部分资料列出如下。试进行整理,作出入托与未入托儿童智能水平及其影响因素的分析(包括显着性检验)、用图表列出分析结果,并写出文字说明,整理时可参阅所附整理表。
儿童智能发育的调查
| 例 号 | 性 别 | 年龄 (岁) | 是否 入托 | 父 亲 文化程度 | 母 亲 文化程度 | 是否 母乳喂养 | 智能 分数 |
| 1 | 男 | 3.6 | 是 | 高小 | 高中 | 否 | 90 |
| 2 | 男 | 5.2 | 是 | 初中 | 初中 | 否 | 110 |
| 3 | 女 | 4.6 | 是 | 初中 | 高中 | 否 | 113 |
| 4 | 女 | 2.2 | 是 | 初中 | 高中 | 否 | 97 |
| 5 | 女 | 3.4 | 是 | 中专 | 初中 | 否 | 120 |
| 6 | 男 | 2.2 | 是 | 中专 | 初中 | 否 | 100 |
| 7 | 女 | 4.7 | 是 | 高中 | 中专 | 否 | 117 |
| 8 | 女 | 4.7 | 是 | 高中 | 初中 | 否 | 100 |
| 9 | 男 | 5.3 | 是 | 高中 | 初中 | 否 | 97 |
| 10 | 女 | 5.0 | 是 | 高中 | 高中 | 否 | 103 |
| 11 | 男 | 1.8 | 是 | 高中 | 高中 | 否 | 93 |
| 12 | 男 | 2.0 | 是 | 高中 | 高中 | 否 | 123 |
| 13 | 男 | 3.3 | 是 | 高中 | 初中 | 否 | 83 |
| 14 | 男 | 1.8 | 是 | 高中 | 高中 | 否 | 93 |
| 15 | 女 | 4.8 | 是 | 大专 | 初中 | 否 | 100 |
| 16 | 女 | 4.5 | 是 | 大专 | 高中 | 否 | 100 |
| 17 | 男 | 5.1 | 是 | 大专 | 高中 | 否 | 100 |
| 18 | 女 | 4.2 | 是 | 大专 | 初中 | 否 | 83 |
| 19 | 男 | 2.3 | 是 | 大专 | 初中 | 否 | 107 |
| 20 | 女 | 2.5 | 是 | 大专 | 高中 | 否 | 117 |
| 21 | 女 | 6.6 | 是 | 大专 | 大专 | 否 | 100 |
| 22 | 女 | 3.0 | 是 | 大专 | 中专 | 否 | 117 |
| 23 | 男 | 6.3 | 是 | 大学 | 大学 | 否 | 113 |
| 24 | 男 | 4.0 | 是 | 大学 | 中专 | 否 | 103 |
| 25 | 女 | 4.1 | 是 | 大学 | 大学 | 否 | 93 |
| 26 | 男 | 5.0 | 是 | 大学 | 初中 | 否 | 90 |
| 27 | 女 | 5.1 | 是 | 大学 | 中专 | 否 | 107 |
| 28 | 男 | 1.6 | 是 | 大学 | 大专 | 否 | 113 |
| 29 | 男 | 4.3 | 是 | 大学 | 中专 | 否 | 90 |
| 30 | 男 | 4.4 | 是 | 大学 | 高中 | 否 | 97 |
| 31 | 女 | 4.4 | 是 | 大学 | 大学 | 否 | 110 |
| 32 | 男 | 2.2 | 是 | 初中 | 初中 | 是 | 118 |
| 33 | 女 | 3.6 | 是 | 初中 | 高中 | 是 | 73 |
| 34 | 男 | 4.8 | 是 | 初中 | 初中 | 是 | 113 |
| 35 | 女 | 5.4 | 是 | 初中 | 初中 | 是 | 90 |
| 36 | 女 | 5.7 | 是 | 初中 | 初中 | 是 | 113 |
| 37 | 男 | 6.2 | 是 | 初中 | y 高中 | 是 | 117 |
| 38 | 女 | 6.2 | 是 | 初中 | 初中 | 是 | 110 |
| 39 | 男 | 3.2 | 是 | 中专 | 大学 | 是 | 100 |
| 40 | 男 | 5.4 | 是 | 中专 | 初中 | 是 | 97 |
| 41 | 男 | 2.7 | 是 | 中专 | 大专 | 是 | 103 |
| 42 | 女 | 3.8 | 是 | 高中 | 高中 | 是 | 110 |
| 43 | 女 | 3.1 | 是 | 高中 | 高中 | 是 | 120 |
| 44 | 女 | 5.4 | 是 | 高中 | 高中 | 是 | 93 |
| 45 | 男 | 5.6 | 是 | 大专 | 大专 | 是 | 90 |
| 46 | 男 | 6.6 | 是 | 大专 | 高小 | 是 | 63 |
| 47 | 男 | 1.9 | 是 | 大学 | 高中 | 是 | 133 |
| 48 | 男 | 3.7 | 是 | 大学 | 高中 | 是 | 93 |
| 49 | 女 | 3.1 | 是 | 大学 | 初中 | 是 | 100 |
| 50 | 男 | 5.5 | 是 | 大学 | 中专 | 是 | 93 |
| 51 | 女 | 3.7 | 是 | 初中 | 高中 | 否 | 80 |
| 52 | 女 | 3.1 | 是 | 初中 | 初中 | 否 | 93 |
| 53 | 男 | 5.2 | 否 | 初中 | 初中 | 否 | 90 |
| 54 | 女 | 4.7 | 否 | 初中 | 初中 | 否 | 107 |
| 55 | 女 | 4.7 | 否 | 初中 | 初中 | 否 | 77 |
| 56 | 男 | 6.2 | 否 | 初中 | 高小 | 否 | 90 |
| 57 | 男 | 6.2 | 否 | 初中 | 初中 | 否 | 100 |
| 58 | 男 | 3.3 | 否 | 高中 | 初中 | 否 | 100 |
| 59 | 女 | 1.1 | 否 | 高中 | 高中 | 否 | 93 |
| 60 | 女 | 2.0 | 否 | 大专 | 大专 | 否 | 100 |
| 61 | 男 | 5.4 | 否 | 高小 | 高小 | 是 | 73 |
| 62 | 女 | 6.2 | 否 | 高小 | 初中 | 是 | 50 |
| 63 | 男 | 5.5 | 否 | 初中 | 初中 | 是 | 63 |
| 64 | 女 | 5.6 | 否 | 初中 | 初中 | 是 | 60 |
| 65 | 女 | 5.7 | 否 | 初中 | 初中 | 是 | 67 |
| 66 | 女 | 2.2 | 否 | 初中 | 高中 | 是 | 90 |
| 67 | 男 | 2.3 | 否 | 初中 | 初中 | 是 | 90 |
| 68 | 女 | 2.4 | 否 | 初中 | 初中 | 是 | 113 |
| 69 | 男 | 2.2 | 否 | 初中 | 初中 | 是 | 90 |
| 70 | 男 | 2.7 | 否 | 初中 | 高中 | 是 | 110 |
| 71 | 男 | 3.0 | 否 | 初中 | 高中 | 是 | 60 |
| 72 | 男 | 1.6 | 否 | 初中 | 高中 | 是 | 110 |
| 73 | 男 | 6.7 | 否 | 初中 | 初中 | 是 | 100 |
| 74 | 女 | 6.9 | 否 | 初中 | 高小 | 是 | 43 |
| 75 | 女 | 3.1 | 否 | 初中 | 初中 | 是 | 60 |
| 76 | 男 | 4.1 | 否 | 初中 | 初中 | 是 | 90 |
| 77 | 男 | 5.3 | 否 | 初中 | 初中 | 是 | 60 |
| 78 | 女 | 3.4 | 否 | 初中 | 高中 | 是 | 73 |
| 79 | 女 | 3.6 | 否 | 初中 | 初中 | 是 | 90 |
| 80 | 男 | 3.6 | 否 | 初中 | 初中 | 是 | 87 |
| 81 | 女 | 4.8 | 否 | 初中 | 初中 | 是 | 93 |
| 82 | 女 | 4.0 | 否 | 初中 | 初中 | 是 | 93 |
| 83 | 男 | 4.5 | 否 | 初中 | 初中 | 是 | 80 |
| 84 | 女 | 4.2 | 否 | 初中 | 高小 | 是 | 77 |
| 85 | 男 | 4.3 | 否 | 初中 | 高中 | 是 | 83 |
| 86 | 女 | 4.4 | 否 | 初中 | 初中 | 是 | 60 |
| 87 | 男 | 4.4 | 否 | 初中 | 初中 | 是 | 73 |
| 88 | 女 | 4.6 | 否 | 初中 | 高中 | 是 | 70 |
| 89 | 男 | 5.1 | 否 | 初中 | 初中 | 是 | 77 |
| 90 | 女 | 5.1 | 否 | 初中 | 高中 | 是 | 63 |
| 91 | 男 | 5.1 | 否 | 初中 | 高中 | 是 | 57 |
| 92 | 男 | 5.1 | 否 | 初中 | 初中 | 是 | 68 |
| 93 | 男 | 5.4 | 否 | 中专 | 高中 | 是 | 93 |
| 94 | 女 | 4.8 | 否 | 高中 | 高中 | 是 | 67 |
| 95 | 男 | 5.4 | 否 | 高中 | 初中 | 是 | 93 |
| 96 | 男 | 3.8 | 否 | 高中 | 初中 | 是 | 63 |
| 97 | 男 | 3.2 | 否 | 高中 | 高中 | 是 | 77 |
| 98 | 女 | 1.2 | 否 | 高中 | 初中 | 是 | 127 |
| 99 | 男 | 1.9 | 否 | 高中 | 初中 | 是 | 110 |
| 100 | 女 | 2.2 | 否 | 高中 | 高小 | 是 | 90 |
附表 1
智能分数与父亲文化程度的关系
| 智能分数 | 初中及以下 | 中专、高中 | 大专、大学 | 合计 |
| 90 以下 | ||||
| 90— | ||||
| 110— | ||||
| 合 计 |
附表 2
智能分数与是否入托的关系
| 例 数 | 智 能 分 数 | |||
| 平均数 | 标准差 | 标准误 | ||
| 入托儿童 | ||||
| 未入托儿章 | ||||
附表 3
智能分数与是否入托、母乳喂养的关系
| 母乳喂养 | 非母乳喂养 | |||
| 例 数 | 智能分数 | 例 数 | 智能分数 | |
| X±SE | X±SE | |||
| 入托儿童 | ||||
| 未入托儿童 | ||||
| 合 计 | ||||
附表 1 x2 值表
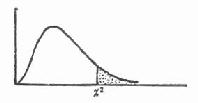
| n' | P | ||||||||||||
| 0.995 | 0.990 | 0.975 | 0.950 | 0.900 | 0.750 | 0.500 | 0.250 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | |
| 1 | … | … | … | … | 0.02 | 0.10 | 0.45 | 1.32 | 2.71 | 3.84 | 5.02 | 6.63 | 7.88 |
| 2 | 0.01 | 0.02 | 0.02 | 0.10 | 0.21 | 0.58 | 1.39 | 2.77 | 4.61 | 5.99 | 7.38 | 9.21 | 10.60 |
| 3 | 0.07 | 0.11 | 0.22 | 0.35 | 0.58 | 1.21 | 2.37 | 4.11 | 6.25 | 7.81 | 9.35 | 11.34 | 12.84 |
| 4 | 0.21 | 0.30 | 0.48 | 0.71 | 1.06 | 1.92 | 3.36 | 5.39 | 7.78 | 9.49 | 11.14 | 13.28 | 14.86 |
| 5 | 0.41 | 0.55 | 0.83 | 1.15 | 1.61 | 2.67 | 4.35 | 6.63 | 9.24 | 11.07 | 12.83 | 15.09 | 16.75 |
| 6 | 0.68 | 0.87 | 1.24 | 1.64 | 2.20 | 3.45 | 5.35 | 7.84 | 10.64 | 12.59 | 14.45 | 16.81 | 18.55 |
| 7 | 0.99 | 1.24 | 1.69 | 2.17 | 2.83 | 4.25 | 6.35 | 9.04 | 12.02 | 14.07 | 16.01 | 18.48 | 20.28 |
| 8 | 1.34 | 1.65 | 2.18 | 2.73 | 3.40 | 5.07 | 7.34 | 10.22 | 13.36 | 15.51 | 17.53 | 20.09 | 21.96 |
| 9 | 1.73 | 2.09 | 2.70 | 3.33 | 4.17 | 5.90 | 8.34 | 11.39 | 14.68 | 16.92 | 19.02 | 21.67 | 23.59 |
| 10 | 2.16 | 2.56 | 3.25 | 3.94 | 4.87 | 6.74 | 9.34 | 12.55 | 15.99 | 18.31 | 20.48 | 23.21 | 25.19 |
| 11 | 2.60 | 3.05 | 3.82 | 4.57 | 5.58 | 7.58 | 10.34 | 13.70 | 17.28 | 19.68 | 21.92 | 24.72 | 26.76 |
| 12 | 3.07 | 3.57 | 4.40 | 5.23 | 6.30 | 8.44 | 11.34 | 14.85 | 18.55 | 21.03 | 23.34 | 26.22 | 28.30 |
| 13 | 3.57 | 4.11 | 5.01 | 5.89 | 7.04 | 9.30 | 12.34 | 15.98 | 19.81 | 22.36 | 24.74 | 27.69 | 29.82 |
| 14 | 4.07 | 4.66 | 5.63 | 6.57 | 7.79 | 10.17 | 13.34 | 17.12 | 21.06 | 23.68 | 26.12 | 29.14 | 31.32 |
| 15 | 4.60 | 5.23 | 6.27 | 7.26 | 8.55 | 11.04 | 14.34 | 18.25 | 22.31 | 25.00 | 27.49 | 30.58 | 32.80 |
| 16 | 5.14 | 5.81 | 6.91 | 7.96 | 9.31 | 11.91 | 15.34 | 19.37 | 23.54 | 26.30 | 28.85 | 32.00 | 34.27 |
| 17 | 5.70 | 6.41 | 7.56 | 8.67 | 10.09 | 12.79 | 16.34 | 20.49 | 24.77 | 27.59 | 30.19 | 33.41 | 35.72 |
| 18 | 6.26 | 7.01 | 8.23 | 9.39 | 10.86 | 13.68 | 17.34 | 21.60 | 25.99 | 28.87 | 31.53 | 34.81 | 37.16 |
| 19 | 6.84 | 7.63 | 8.91 | 10.12 | 11.65 | 14.56 | 18.34 | 22.72 | 27.20 | 30.14 | 32.85 | 36.19 | 38.58 |
| 20 | 7.43 | 8.26 | 9.59 | 10.85 | 12.44 | 15.45 | 19.34 | 23.83 | 28.41 | 31.41 | 34.17 | 37.57 | 40.00 |
| 21 | 8.03 | 8.90 | 10.28 | 11.59 | 13.24 | 16.34 | 20.34 | 24.93 | 29.62 | 32.67 | 35.48 | 38.93 | 41.40 |
| 22 | 8.64 | 9.54 | 10.98 | 12.34 | 14.04 | 17.24 | 21.34 | 26.04 | 30.81 | 33.92 | 36.78 | 40.29 | 42.80 |
| 23 | 9.26 | 10.20 | 11.69 | 13.09 | 14.85 | 18.14 | 22.34 | 27.14 | 32.01 | 35.17 | 38.08 | 41.64 | 44.18 |
| 24 | 9.89 | 10.86 | 12.40 | 13.85 | 15.66 | 19.04 | 23.34 | 28.24 | 33.20 | 36.42 | 39.36 | 42.98 | 45.56 |
| 25 | 10.52 | 11.52 | 13.12 | 14.61 | 16.47 | 19.94 | 24.34 | 29.34 | 34.38 | 37.65 | 40.65 | 44.31 | 46.93 |
| 26 | 11.16 | 12.20 | 13.84 | 15.38 | 17.29 | 20.84 | 25.34 | 30.43 | 35.56 | 38.89 | 41.92 | 45.64 | 48.29 |
| 27 | 11.81 | 12.88 | 14.57 | 16.15 | 18.11 | 21.75 | 26.34 | 31.53 | 36.74 | 40.11 | 43.19 | 46.96 | 49.64 |
| 28 | 12.46 | 13.56 | 15.31 | 16.93 | 18.94 | 22.66 | 27.34 | 32.62 | 37.92 | 41.34 | 44.46 | 48.28 | 50.99 |
| 29 | 13.12 | 14.26 | 16.05 | 17.71 | 19.77 | 23.57 | 28.34 | 33.71 | 39.09 | 42.56 | 45.72 | 49.59 | 52.34 |
| 30 | 13.79 | 14.95 | 16.79 | 18.49 | 20.60 | 24.48 | 29.34 | 34.80 | 40.26 | 43.77 | 46.98 | 50.89 | 53.67 |
| 40 | 20.71 | 22.16 | 24.43 | 26.51 | 29.05 | 33.66 | 39.34 | 45.62 | 51.80 | 55.76 | 59.34 | 63.69 | 66.77 |
| 50 | 27.99 | 29.71 | 32.36 | 34.76 | 37.69 | 42.94 | 49.33 | 56.33 | 63.17 | 67.50 | 71.42 | 76.15 | 79.49 |
| 60 | 35.53 | 37.48 | 40.48 | 43.19 | 46.46 | 52.29 | 59.33 | 66.98 | 74.40 | 79.08 | 83.30 | 88.38 | 91.95 |
| 70 | 43.28 | 45.44 | 48.76 | 51.74 | 55.33 | 61.70 | 69.33 | 77.58 | 85.53 | 90.53 | 95.02 | 100.42 | 104.22 |
| 80 | 51.17 | 53.54 | 57.15 | 60.39 | 64.28 | 71.14 | 79.33 | 88.13 | 96.58 | 101.88 | 106.63 | 112.33 | 116.32 |
| 90 | 59.20 | 61.75 | 65.65 | 69.13 | 73.29 | 80.62 | 89.33 | 98.64 | 107.56 | 113.14 | 118.14 | 124.12 | 128.30 |
| 100 | 67.33 | 70.06 | 74.22 | 77.93 | 82.36 | 90.13 | 99.33 | 109.14 | 118.50 | 124.34 | 129.56 | 135.81 | 140.17 |
注:自由度的符号本书统一用 ν,但若沿用 n’也不为错。
附表 2 标准正态曲线下的面积表
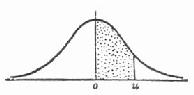
| u | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0.0 | .0000 | .0040 | .0080 | .0120 | .0160 | .0199 | .0239 | .0276 | .0319 | .0359 |
| 0.1 | .0398 | .0438 | .0478 | .0517 | .0557 | .0596 | .0636 | .0675 | .0714 | .0754 |
| 0.2 | .0793 | .0832 | .0871 | .0910 | .0948 | .0987 | .1026 | .1064 | .1103 | .1141 |
| 0.3 | .1179 | .1217 | .1255 | .1293 | .1331 | .1368 | .1406 | .1443 | .1480 | .1517 |
| 0.4 | .1554 | .1591 | .1628 | .1664 | .1700 | .1736 | .1772 | .1808 | .1844 | .1879 |
| 0.5 | .1915 | .1950 | .1985 | .2019 | .2054 | .2088 | .2123 | .2157 | .2190 | .2224 |
| 0.6 | .2258 | .2291 | .2324 | .2357 | .2389 | .2422 | .2454 | .2486 | .2518 | .2549 |
| 0.7 | .2580 | .2612 | .2642 | .2673 | .2704 | .2734 | .2764 | .2794 | .2823 | .2852 |
| 0.8 | .2881 | .2910 | .2939 | .2967 | .2996 | .3023 | .3051 | .3078 | .3106 | .3133 |
| 0.9 | .3159 | .3186 | .3212 | .3238 | .3264 | .3289 | .3316 | .3340 | .3365 | .3389 |
| 1.0 | .3413 | .3438 | .3461 | .3485 | .3508 | .3531 | .3554 | .3577 | .3599 | .3621 |
| 1.1 | .3643 | .3665 | .3686 | .3708 | .3729 | .3749 | .3770 | .3790 | .3810 | .3830 |
| 1.2 | .3849 | .3869 | .3888 | .3907 | .3925 | .3944 | .3962 | .3980 | .3997 | .4015 |
| 1.3 | .4032 | .4049 | .4066 | .4082 | .4099 | .4115 | .4131 | .4147 | .4162 | .4177 |
| 1.4 | .4192 | .4207 | .4222 | .4236 | .4251 | .4265 | .4270 | .4292 | .4306 | .4319 |
| 1.5 | .4332 | .4345 | .4357 | .4370 | .4382 | .4394 | .4406 | .4418 | .4429 | .4441 |
| 1.6 | .4452 | .4463 | .4474 | .4484 | .4495 | .4505 | .4515 | .4525 | .4535 | .4545 |
| 1.7 | .4554 | .4564 | .4573 | .4582 | .4591 | .4599 | .4608 | .4616 | .4625 | .4633 |
| 1.8 | .4641 | .4649 | .4656 | .4664 | .4671 | .4678 | .4686 | .4693 | .4699 | .4706 |
| 1.9 | .4713 | .4719 | .4726 | .4732 | .4733 | .4744 | .4750 | .4756 | .4761 | .4767 |
| 2.0 | .4772 | .4778 | .4783 | .4788 | .4793 | .4798 | .4803 | .4808 | .4812 | .4817 |
| 2.1 | .4821 | .4826 | .4830 | .4834 | .4838 | .4842 | .4846 | .4850 | .4854 | .4857 |
| 2.2 | .4861 | .4864 | .4868 | .4871 | .4875 | .4878 | .4881 | .4884 | .4887 | .4890 |
| 2.3 | .4893 | .4896 | .4898 | .4901 | .4904 | .4906 | .4909 | .4911 | .4913 | .4916 |
| 2.4 | .4918 | .4920 | .4922 | .4925 | .4927 | .4929 | .4931 | .4932 | .4934 | .4936 |
| 2.5 | .4938 | .4940 | .4941 | .4943 | .4945 | .4946 | .4948 | .4949 | .4951 | .4952 |
| 2.6 | .4953 | .4955 | .4956 | .4957 | .4959 | .4960 | .4961 | .4962 | .4963 | .4964 |
| 2.7 | .4965 | .4966 | .4967 | .4968 | .4960 | .4970 | .4971 | .4972 | .4973 | .4974 |
| 2.8 | .4974 | .4975 | .4976 | .4977 | .4977 | .4978 | .4979 | .4979 | .4980 | .4981 |
| 2.9 | .4981 | .4982 | .4982 | .4983 | .4984 | .4984 | .4985 | .4985 | .4986 | .4986 |
| 3.0 | .4987 | .4987 | .4987 | .4988 | .4998 | .4989 | .4989 | .4989 | .4990 | .4990 |
| 3.1 | .4990 | .4991 | .4991 | .4991 | .4992 | .4992 | .4992 | .4992 | .4993 | .4993 |
| 3.2 | .4993 | .4993 | .4994 | .4994 | .4994 | .4994 | .4994 | .4995 | .4995 | .4995 |
| 3.3 | .4995 | .4995 | .4995 | .4996 | .4996 | .4996 | .4996 | .4996 | .4996 | .4997 |
| 3.4 | .4997 | .4997 | .4997 | .4997 | .4997 | .4997 | .4907 | .4997 | .4997 | .4998 |
| 3.5 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 | .4998 |
| 3.6 | .4998 | .4998 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 |
| 3.7 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 |
| 3.8 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 | .4999 |
| 3.9 | .5000 | .5000 | .5000 | .5000 | .5000 | .5000 | .5000 | .5000 | .5000 | .5000 |
附表 3 t 值表
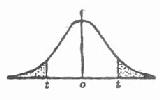
| n’ | P(2): P(1): | 0.50 0.25 | 0.20 0.10 | 0.10 0.05 | 0.05 0.025 | 0.02 0.01 | 0.01 0.005 | 0.005 0.0025 | 0.002 0.001 | 0.001 0.0005 | |
| 1 | 1.000 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 | 127.321 | 318.309 | 636.619 | ||
| 2 | 0.816 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.089 | 22.327 | 31.599 | ||
| 3 | 0.765 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.215 | 12.924 | ||
| 4 | 0.741 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 | ||
| 5 | 0.727 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 | ||
| 6 | 0.718 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 | ||
| 7 | 0.711 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 | ||
| 8 | 0.706 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 | ||
| 9 | 0.703 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 | ||
| 10 | 0.700 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 | ||
| 11 | 0.697 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 | ||
| 12 | 0.695 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 | ||
| 13 | 0.694 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 | ||
| 14 | 0.692 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 | ||
| 15 | 0.691 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 | ||
| 16 | 0.690 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 | ||
| 17 | 0.689 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 | ||
| 18 | 0.688 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 | ||
| 19 | 0.688 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 | ||
| 20 | 0.687 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 | ||
| 21 | 0.686 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 | ||
| 22 | 0.686 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 | ||
| 23 | 0.685 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.768 | ||
| 24 | 0.685 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 | ||
| 25 | 0.684 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 | ||
| 26 | 0.684 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 | ||
| 27 | 0.684 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 | ||
| 28 | 0.683 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 | ||
| 29 | 0.683 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 | ||
| 30 | 0.683 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 | ||
| 31 | 0.682 | 1.309 | 1.696 | 2.040 | 2.453 | 2.744 | 3.022 | 3.375 | 3.633 | ||
| 32 | 0.682 | 1.309 | 1.694 | 2.037 | 2.449 | 2.738 | 3.015 | 3.365 | 3.622 | ||
| 33 | 0.682 | 1.308 | 1.692 | 2.035 | 2.445 | 2.733 | 3.008 | 3.356 | 3.611 | ||
| 34 | 0.682 | 1.307 | 1.091 | 2.032 | 2.441 | 2.728 | 3.002 | 3.348 | 3.601 | ||
| 35 | 0.682 | 1.306 | 1.690 | 2.030 | 2.438 | 2.724 | 2.996 | 3.340 | 3.591 | ||
| 36 | 0.681 | 1.306 | 1.688 | 2.028 | 2.434 | 2.719 | 2.990 | 3.333 | 3.582 | ||
| 37 | 0.681 | 1.305 | 1.687 | 2.026 | 2.431 | 2.715 | 2.985 | 3.326 | 3.574 | ||
| 38 | 0.681 | 1.304 | 1.686 | 2.024 | 2.429 | 2.712 | 2.980 | 3.319 | 3.566 | ||
| 39 | 0.681 | 1.304 | 1.685 | 2.023 | 2.426 | 2.708 | 2.976 | 3.313 | 3.558 | ||
| 40 | 0.681 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 | ||
| 50 | 0.679 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 | ||
| 60 | 0.679 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 | ||
| 70 | 0.678 | 1.294 | 1.667 | 1.994 | 2.381 | 2.648 | 2.899 | 3.211 | 3.436 | ||
| 80 | 0.678 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 | ||
| 90 | 0.677 | 1.291 | 1.662 | 1.987 | 2.368 | 2.632 | 2.878 | 3.183 | 3.402 | ||
| 100 | 0.677 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 | ||
| 200 | 0.676 | 1.286 | 1.653 | 1.972 | 2.345 | 2.601 | 2.839 | 3.131 | 3.340 | ||
| 500 | 0.675 | 1.283 | 1.648 | 1.965 | 2.334 | 2.586 | 2.820 | 3.107 | 3.310 | ||
| 1000 | 0.675 | 1.282 | 1.646 | 1.962 | 2.330 | 2.581 | 2.813 | 3.098 | 3.300 | ||
| ∝ | 0.6745 | 1.2816 | 1.6449 | 1.9600 | 2.3263 | 2.5758 | 2.8070 | 3.0902 | 3.2905 | ||
注:表上右上角图中的阴影部分表示概率 P,P(2)是双侧的概率,P(1)是单侧的概率,n’是自由度。
附表 4 百分比的 95% 与 99% 可信区间
| 观察数 f | 95% 可信区间 | 99% 可信区间 | ||||||||||||||
| 样本大小,n | 样本大小,n | |||||||||||||||
| 10 | 15 | 20 | 30 | 10 | 15 | 20 | 30 | |||||||||
| 31 | 22 | 17 | 20 | 41 | 30 | 23 | 16 | |||||||||
| 1 | 45 | 32 | 25 | 17 | 54 | 40 | 32 | 22 | ||||||||
| 2 | 3 | 56 | 2 | 40 | 1 | 31 | 1 | 22 | 1 | 65 | 1 | 49 | 1 | 39 | 28 | |
| 3 | 7 | 65 | 4 | 48 | 3 | 38 | 2 | 27 | 4 | 24 | 2 | 56 | 2 | 45 | 1 | 32 |
| 4 | 12 | 74 | 8 | 55 | 6 | 44 | 4 | 31 | 8 | 81 | 5 | 63 | 4 | 51 | 3 | 36 |
| 5 | 19 | 81 | 12 | 62 | 9 | 49 | 6 | 35 | 13 | 87 | 8 | 69 | 6 | 56 | 4 | 40 |
| 6 | 26 | 88 | 16 | 68 | 12 | 54 | 8 | 39 | 19 | 92 | 12 | 74 | 8 | 61 | 6 | 44 |
| 7 | 35 | 93 | 21 | 73 | 15 | 59 | 10 | 43 | 26 | 96 | 16 | 79 | 11 | 66 | 8 | 48 |
| 8 | 44 | 97 | 27 | 79 | 19 | 64 | 12 | 46 | 35 | 99 | 21 | 84 | 15 | 70 | 10 | 52 |
| 9 | 55 | 100 | 32 | 84 | 23 | 68 | 15 | 50 | 46 | 100 | 26 | 88 | 18 | 74 | 12 | 55 |
| 10 | 69 | 100 | 38 | 88 | 27 | 73 | 17 | 53 | 59 | 100 | 31 | 92 | 22 | 78 | 14 | 58 |
| 11 | 45 | 92 | 32 | 77 | 20 | 56 | 37 | 95 | 26 | 82 | 16 | 62 | ||||
| 12 | 52 | 96 | 36 | 81 | 23 | 60 | 44 | 98 | 30 | 85 | 18 | 65 | ||||
| 13 | 60 | 98 | 41 | 85 | 25 | 63 | 51 | 99 | 34 | 89 | 21 | 68 | ||||
| 14 | 68 | 100 | 46 | 88 | 28 | 66 | 60 | 100 | 39 | 92 | 24 | 71 | ||||
| 15 | 78 | 100 | 51 | 91 | 31 | 69 | 70 | 100 | 44 | 94 | 26 | 74 | ||||
| 16 | 56 | 94 | 34 | 72 | 49 | 96 | 29 | 76 | ||||||||
| 17 | 62 | 97 | 37 | 75 | 55 | 98 | 32 | 79 | ||||||||
| 18 | 69 | 99 | 40 | 77 | 61 | 99 | 35 | 82 | ||||||||
| 19 | 75 | 100 | 44 | 80 | 68 | 100 | 38 | 84 | ||||||||
| 20 | 83 | 100 | 47 | 83 | 77 | 100 | 42 | 86 | ||||||||
| 21 | 50 | 85 | 45 | 88 | ||||||||||||
| 22 | 54 | 88 | 48 | 90 | ||||||||||||
| 23 | 57 | 90 | 52 | 92 | ||||||||||||
| 24 | 61 | 92 | 56 | 94 | ||||||||||||
| 25 | 65 | 94 | 60 | 96 | ||||||||||||
| 26 | 69 | 96 | 64 | 97 | ||||||||||||
| 27 | 73 | 98 | 68 | 99 | ||||||||||||
| 28 | 78 | 99 | 72 | 100 | ||||||||||||
| 29 | 83 | 100 | 78 | 100 | ||||||||||||
| 30 | 88 | 100 | 84 | 100 | ||||||||||||
注:表中观察数 f 为调查例中查 n 到实验发生某现象的个数。
附表 5 W 检验 ain 系数表
| i | n | |||||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||
| 1 | 0.7071 | 0.7071 | 0.6872 | 0.6646 | 0.6431 | 0.6233 | 0.6052 | 0.5888 | 0.5739 | |||||||||
| 2 | - | 0.0000 | 0.1677 | 0.2413 | 0.2806 | 0.3031 | 0.3164 | 0.3244 | 0.3291 | |||||||||
| 3 | - | - | - | 0.0000 | 0.0875 | 0.1401 | 0.1743 | 0.1976 | 0.2141 | |||||||||
| 4 | - | - | - | - | - | 0.0000 | 0.0561 | 0.0947 | 0.1224 | |||||||||
| 5 | - | - | - | - | - | - | - | 0.0000 | 0.0399 | |||||||||
| n | ||||||||||||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |||||||||
| 1 | 0.5601 | 0.5475 | 0.5359 | 0.5251 | 0.5150 | 0.5056 | 0.4968 | 0.4886 | 0.4808 | 0.4734 | ||||||||
| 2 | 0.3315 | 0.3325 | 0.3325 | 0.3318 | 0.3306 | 0.3290 | 0.3273 | 0.3253 | 0.3232 | 0.3211 | ||||||||
| 3 | 0.2260 | 0.2347 | 0.2412 | 0.2460 | 0.2495 | 0.2521 | 0.2540 | 0.2553 | 0.2561 | 0.2565 | ||||||||
| 4 | 0.1429 | 0.1586 | 0.1707 | 0.1802 | 0.1878 | 0.1939 | 0.1988 | 0.2027 | 0.2059 | 0.2085 | ||||||||
| 5 | 0.0695 | 0.0922 | 0.1099 | 0.1240 | 0.1353 | 0.1447 | 0.1524 | 0.1587 | 0.1641 | 0.1686 | ||||||||
| 6 | 0.0000 | 0.0303 | 0.0539 | 0.0727 | 0.0880 | 0.1005 | 0.1109 | 0.1197 | 0.1271 | 0.1334 | ||||||||
| 7 | - | - | 0.0000 | 0.0240 | 0.0433 | 0.0593 | 0.0725 | 0.0837 | 0.0932 | 0.1013 | ||||||||
| 8 | - | - | - | - | 0.0000 | 0.0196 | 0.0359 | 0.0496 | 0.0612 | 0.0711 | ||||||||
| 9 | - | - | - | - | - | - | 0.0000 | 0.0163 | 0.0303 | 0.0422 | ||||||||
| 10 | - | - | - | - | - | - | - | - | 0.0000 | 0.0140 | ||||||||
| i | n | |||||||||||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |||||||||
| 1 | 0.4643 | 0.4590 | 0.4542 | 0.4493 | 0.4450 | 0.4407 | 0.4366 | 0.4328 | 0.4291 | 0.4254 | ||||||||
| 2 | 0.3158 | 0.3156 | 0.3126 | 0.3098 | 0.3069 | 0.3043 | 0.3018 | 0.2992 | 0.2968 | 0.2944 | ||||||||
| 3 | 0.2578 | 0.2571 | 0.2563 | 0.2554 | 0.2543 | 0.2533 | 0.2522 | 0.2510 | 0.2499 | 0.2487 | ||||||||
| 4 | 0.2119 | 0.2131 | 0.2139 | 0.2145 | 0.2148 | 0.2151 | 0.2152 | 0.2151 | 0.2150 | 0.2148 | ||||||||
| 5 | 0.1736 | 0.1764 | 0.1787 | 0.1807 | 0.1822 | 0.1836 | 0.1848 | 0.1857 | 0.1864 | 0.1870 | ||||||||
| 6 | 0.1399 | 0.1443 | 0.1480 | 0.1512 | 0.1539 | 0.1563 | 0.1584 | 0.1601 | 0.1616 | 0.1630 | ||||||||
| 7 | 0.1092 | 0.1150 | 0.1201 | 0.1245 | 0.1283 | 0.1316 | 0.1346 | 0.1372 | 0.1395 | 0.1415 | ||||||||
| 8 | 0.0804 | 0.0878 | 0.0941 | 0.0997 | 0.1046 | 0.1089 | 0.1128 | 0.1162 | 0.1192 | 0.1219 | ||||||||
| 9 | 0.0530 | 0.0618 | 0.0696 | 0.0764 | 0.0823 | 0.0876 | 0.0923 | 0.0965 | 0.1002 | 0.1036 | ||||||||
| 10 | 0.0263 | 0.0368 | 0.0459 | 0.0539 | 0.0610 | 0.0672 | 0.0728 | 0.0778 | 0.0822 | 0.0862 | ||||||||
| 11 | 0.0000 | 0.0122 | 0.0228 | 0.0321 | 0.0403 | 0.0476 | 0.0540 | 0.0598 | 0.0650 | 0.0697 | ||||||||
| 12 | - | - | 0.0000 | 0.0107 | 0.0200 | 0.0284 | 0.0358 | 0.0424 | 0.0483 | 0.0537 | ||||||||
| 13 | - | - | - | - | 0.0000 | 0.0094 | 0.0178 | 0.0253 | 0.0320 | 0.0381 | ||||||||
| 14 | - | - | - | - | - | - | 0.0000 | 0.0084 | 0.0159 | 0.0227 | ||||||||
| 15 | - | - | - | - | - | - | - | - | 0.0000 | 0.0076 | ||||||||
| i | n | |||||||||||||||||
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | |||||||||
| 1 | 0.4220 | 0.4188 | 0.4156 | 0.4127 | 0.4096 | 0.4068 | 0.4040 | 0.4015 | 0.3989 | 0.3964 | ||||||||
| 2 | 0.2921 | 0.2829 | 0.2876 | 0.2854 | 0.2834 | 0.2813 | 0.2794 | 0.2774 | 0.2755 | 0.2737 | ||||||||
| 3 | 0.2475 | 0.2463 | 0.2451 | 0.2439 | 0.2427 | 0.2415 | 0.2403 | 0.2391 | 0.2380 | 0.2368 | ||||||||
| 4 | 0.2145 | 0.2141 | 0.2137 | 0.2132 | 0.2127 | 0.2121 | 0.2116 | 0.2110 | 0.2104 | 0.2098 | ||||||||
| 5 | 0.1874 | 0.1878 | 0.1880 | 0.1882 | 0.1883 | 0.1883 | 0.1883 | 0.1881 | 0.1880 | 0.1878 | ||||||||
| 6 | 0.1641 | 0.1651 | 0.1660 | 0.1667 | 0.1673 | 0.1678 | 0.1683 | 0.1686 | 0.1689 | 0.1691 | ||||||||
| 7 | 0.1433 | 0.1449 | 0.1463 | 0.1475 | 0.1487 | 0.1496 | 0.1505 | 0.1513 | 0.1520 | 0.1526 | ||||||||
| 8 | 0.1243 | 0.1265 | 0.1284 | 0.1301 | 0.1317 | 0.1331 | 0.1344 | 0.1356 | 0.1366 | 0.1376 | ||||||||
| 9 | 0.1066 | 0.1093 | 0.1118 | 0.1140 | 0.1160 | 0.1179 | 0.1196 | 0.1211 | 0.1225 | 0.1237 | ||||||||
| 10 | 0.0899 | 0.0931 | 0.0961 | 0.0988 | 0.1013 | 0.1036 | 0.1056 | 0.1075 | 0.1092 | 0.1108 | ||||||||
| 11 | 0.0739 | 0.0777 | 0.0812 | 0.0844 | 0.0873 | 0.0900 | 0.0924 | 0.0947 | 0.0967 | 0.0986 | ||||||||
| 12 | 0.0585 | 0.0629 | 0.0669 | 0.0706 | 0.0739 | 0.0770 | 0.0798 | 0.0824 | 0.0848 | 0.0870 | ||||||||
| 13 | 0.0435 | 0.0485 | 0.0530 | 0.0572 | 0.0610 | 0.0645 | 0.0677 | 0.0706 | 0.0733 | 0.0759 | ||||||||
| 14 | 0.0289 | 0.0344 | 0.0395 | 0.0441 | 0.0484 | 0.0523 | 0.0559 | 0.0592 | 0.0622 | 0.0651 | ||||||||
| 15 | 0.0144 | 0.0206 | 0.0262 | 0.0314 | 0.0361 | 0.0404 | 0.0444 | 0.0481 | 0.0515 | 0.0546 | ||||||||
| 16 | 0.0000 | 0.0068 | 0.0131 | 0.0187 | 0.0239 | 0.0287 | 0.0331 | 0.0372 | 0.0409 | 0.0444 | ||||||||
| 17 | - | - | 0.0000 | 0.0062 | 0.0119 | 0.0172 | 0.0220 | 0.0264 | 0.0305 | 0.0343 | ||||||||
| 18 | - | - | - | - | 0.0000 | 0.0057 | 0.0110 | 0.0158 | 0.0203 | 0.0244 | ||||||||
| 19 | - | - | - | - | - | - | 0.0000 | 0.0053 | 0.0101 | 0.0146 | ||||||||
| 20 | - | - | - | - | - | - | - | - | 0.0000 | 0.0049 | ||||||||
| n | ||||||||||||||||||
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | |||||||||
| 1 | 0.3940 | 0.3917 | 0.3894 | 0.3872 | 0.3850 | 0.3830 | 0.3808 | 0.3789 | 0.3770 | 0.3751 | ||||||||
| 2 | 0.2719 | 0.2701 | 0.2684 | 0.2667 | 0.2651 | 0.2635 | 0.2620 | 0.2604 | 0.2589 | 0.2574 | ||||||||
| 3 | 0.2357 | 0.2345 | 0.2334 | 0.2323 | 0.2313 | 0.2302 | 0.2291 | 0.2281 | 0.2271 | 0.2260 | ||||||||
| 4 | 0.2091 | 0.2085 | 0.2078 | 0.2072 | 0.2065 | 0.2058 | 0.2052 | 0.2045 | 0.2038 | 0.2032 | ||||||||
| 5 | 0.1876 | 0.1874 | 0.1871 | 0.1868 | 0.1865 | 0.1862 | 0.1859 | 0.1855 | 0.1851 | 0.1847 | ||||||||
| 6 | 0.1693 | 0.1694 | 0.1695 | 0.1695 | 0.1695 | 0.1695 | 0.1695 | 0.1693 | 0.1692 | 0.1691 | ||||||||
| 7 | 0.1531 | 0.1535 | 0.1539 | 0.1542 | 0.1545 | 0.1548 | 0.1550 | 0.1551 | 0.1553 | 0.1554 | ||||||||
| 8 | 0.1384 | 0.1392 | 0.1398 | 0.1405 | 0.1410 | 0.1415 | 0.1420 | 0.1423 | 0.1427 | 0.1430 | ||||||||
| 9 | 0.1249 | 0.1259 | 0.1269 | 0.1278 | 0.1286 | 0.1293 | 0.1300 | 0.1306 | 0.1312 | 0.1317 | ||||||||
| 10 | 0.1123 | 0.1136 | 0.1149 | 0.1160 | 0.1170 | 0.1180 | 0.1189 | 0.1197 | 0.1205 | 0.1212 | ||||||||
| 11 | 0.1004 | 0.1020 | 0.1035 | 0.1049 | 0.1062 | 0.1073 | 0.1085 | 0.1095 | 0.1105 | 0.1113 | ||||||||
| 12 | 0.0891 | 0.0909 | 0.0927 | 0.0943 | 0.0959 | 0.0972 | 0.0986 | 0.0998 | 0.1010 | 0.1020 | ||||||||
| 13 | 0.0782 | 0.0804 | 0.0824 | 0.0842 | 0.0860 | 0.0876 | 0.0892 | 0.0906 | 0.0919 | 0.0932 | ||||||||
| 14 | 0.0677 | 0.0701 | 0.0724 | 0.0745 | 0.0765 | 0.0783 | 0.0801 | 0.0817 | 0.0832 | 0.0846 | ||||||||
| 15 | 0.0575 | 0.0602 | 0.0628 | 0.0651 | 0.0673 | 0.0694 | 0.0713 | 0.0731 | 0.0748 | 0.0764 | ||||||||
| 16 | 0.0476 | 0.0506 | 0.0534 | 0.0560 | 0.0584 | 0.0607 | 0.0628 | 0.0648 | 0.0667 | 0.0685 | ||||||||
| 17 | 0.0379 | 0.0411 | 0.0442 | 0.0471 | 0.0497 | 0.0522 | 0.0546 | 0.0568 | 0.0588 | 0.0608 | ||||||||
| 18 | 0.0283 | 0.0318 | 0.0352 | 0.0383 | 0.0412 | 0.0439 | 0.0465 | 0.0489 | 0.0511 | 0.0532 | ||||||||
| 19 | 0.0188 | 0.0227 | 0.0263 | 0.0296 | 0.0328 | 0.0357 | 0.0385 | 0.0411 | 0.0436 | 0.0459 | ||||||||
| 20 | 0.0094 | 0.0136 | 0.0175 | 0.0211 | 0.0245 | 0.0277 | 0.0307 | 0.0335 | 0.0361 | 0.0386 | ||||||||
| 21 | 0.0000 | 0.0045 | 0.0087 | 0.0126 | 0.0163 | 0.0197 | 0.0229 | 0.0259 | 0.0288 | 0.0314 | ||||||||
| 22 | - | - | 0.0000 | 0.0042 | 0.0081 | 0.0118 | 0.0153 | 0.0185 | 0.0215 | 0.0244 | ||||||||
| 23 | - | - | - | - | 0.0000 | 0.0039 | 0.0076 | 0.0111 | 0.0143 | 0.0174 | ||||||||
| 24 | - | - | - | - | - | - | 0.0000 | 0.0037 | 0.0071 | 0.0104 | ||||||||
| 25 | - | - | - | - | - | - | - | - | 0.0000 | 0.0035 | ||||||||
附表 6 W 检验界值表
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| α=10.0% | 0.787 | 0.792 | 0.806 | 0.826 | 0.838 | 0.851 | 0.859 | 0.869 | 0.876 | 0.883 | 0.889 | 0.895 |
| α=5.0% | 0.767 | 0.748 | 0.762 | 0.788 | 0.803 | 0.818 | 0.829 | 0.842 | 0.850 | 0.859 | 0.866 | 0.874 |
| α=1.0% | 0.753 | 0.687 | 0.686 | 0.713 | 0.730 | 0.749 | 0.764 | 0.781 | 0.792 | 0.805 | 0.814 | 0.825 |
| n | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| α=10.0% | 0.901 | 0.906 | 0.910 | 0.914 | 0.917 | 0.920 | 0.923 | 0.926 | 0.928 | 0.930 | 0.931 | 0.933 |
| α=5.0% | 0.881 | 0.887 | 0.892 | 0.897 | 0.901 | 0.905 | 0.908 | 0.911 | 0.914 | 0.916 | 0.918 | 0.920 |
| α=1.0% | 0.835 | 0.844 | 0.851 | 0.858 | 0.863 | 0.868 | 0.873 | 0.878 | 0.881 | 0.884 | 0.888 | 0.891 |
| n | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
| α=1.00% | 0.935 | 0.936 | 0.937 | 0.930 | 0.940 | 0.941 | 0.942 | 0.943 | 0.944 | 0.945 | 0.946 | 0.947 |
| α=5.0% | 0.923 | 0.924 | 0.926 | 0.927 | 0.929 | 0.930 | 0.931 | 0.933 | 0.934 | 0.935 | 0.936 | 0.938 |
| α=1.0% | 0.894 | 0.896 | 0.898 | 0.900 | 0.902 | 0.904 | 0.906 | 0.908 | 0.910 | 0.912 | 0.914 | 0.916 |
| n | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| α=10.0% | 0.948 | 0.949 | 0.950 | 0.951 | 0.951 | 0.952 | 0.953 | 0.953 | 0.954 | 0.954 | 0.955 | 0.955 |
| α=5.0% | 0.939 | 0.940 | 0.941 | 0.942 | 0.943 | 0.944 | 0.945 | 0.945 | 0.946 | 0.947 | 0.947 | 0.947 |
| α=1.0% | 0.917 | 0.919 | 0.920 | 0.922 | 0.923 | 0.924 | 0.926 | 0.927 | 0.928 | 0.929 | 0.929 | 0.930 |
附表 7 F 值表(方差齐性检验用)
P=0.05(双侧)
| rˊ | rˊ(较大均方的自由度) | n2ˊ | ||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 30 | 60 | 00 | ||
| 1 | 799 | 364 | 899 | 922 | 937 | 948 | 957 | 963 | 969 | 977 | 985 | 993 | 1001 | 1010 | 1018 | 1 |
| 2 | 39.0 | 39.2 | 39.2 | 39.3 | 39.3 | 39.3 | 39.4 | 39.4 | 39.4 | 39.4 | 39.4 | 39.4 | 39.5 | 39.5 | 39.5 | 2 |
| 3 | 10.0 | 15.4 | 15.1 | 14.9 | 14.7 | 14.6 | 14.5 | 14.5 | 14.4 | 14.3 | 14.2 | 14.2 | 14.1 | 14.0 | 13.9 | 3 |
| 4 | 10.6 | 9.98 | 9.60 | 9.36 | 9.20 | 9.07 | 8.98 | 8.90 | 8.84 | 8.75 | 8.66 | 8.56 | 8.46 | 8.36 | 8.26 | 4 |
| 5 | 8.43 | 7.76 | 7.39 | 7.16 | 6.98 | 6.85 | 6.76 | 6.68 | 6.62 | 6.52 | 6.43 | 6.33 | 6.23 | 6.12 | 6.01 | 5 |
| 6 | 7.26 | 6.60 | 5.23 | 5.99 | 5.82 | 5.69 | 5.60 | 5.52 | 5.46 | 5.37 | 5.27 | 5.17 | 5.06 | 4.96 | 4.85 | 6 |
| 7 | 6.54 | 5.89 | 5.52 | 5.28 | 5.12 | 4.99 | 4.90 | 4.82 | 4.76 | 4.67 | 4.57 | 4.47 | 4.36 | 4.25 | 4.14 | 7 |
| 8 | 6.06 | 5.42 | 5.05 | 4.82 | 4.65 | 4.53 | 4.43 | 4.36 | 4.29 | 4.20 | 4.10 | 4.00 | 3.89 | 3.78 | 3.67 | 8 |
| 9 | 5.71 | 5.08 | 4.72 | 4.48 | 4.32 | 4.20 | 4.10 | 4.03 | 3.96 | 3.87 | 3.77 | 3.67 | 3.56 | 3.45 | 3.33 | 9 |
| 10 | 5.46 | 4.83 | 4.47 | 4.24 | 4.07 | 3.95 | 3.85 | 3.78 | 3.72 | 3.62 | 3.52 | 3.42 | 3.31 | 3.20 | 3.08 | 10 |
| 11 | 5.26 | 4.63 | 4.27 | 4.04 | 3.88 | 3.76 | 3.66 | 3.59 | 3.53 | 3.43 | 3.33 | 3.23 | 3.12 | 3.00 | 2.88 | 11 |
| 12 | 5.10 | 4.47 | 4.12 | 3.89 | 3.73 | 3.61 | 3.51 | 3.44 | 3.37 | 3.28 | 3.18 | 3.07 | 2.96 | 2.85 | 2.72 | 12 |
| 13 | 4.96 | 4.35 | 4.00 | 3.77 | 3.60 | 3.48 | 3.39 | 3.31 | 3.25 | 3.15 | 3.05 | 2.95 | 2.84 | 2.72 | 2.59 | 13 |
| 14 | 4.86 | 4.24 | 3.89 | 3.66 | 3.50 | 3.38 | 3.28 | 3.21 | 3.15 | 3.05 | 2.95 | 2.84 | 2.73 | 2.61 | 2.49 | 14 |
| 15 | 4.76 | 4.15 | 3.80 | 3.58 | 3.41 | 3.29 | 3.20 | 3.12 | 3.06 | 2.96 | 2.86 | 2.76 | 2.64 | 2.52 | 2.39 | 15 |
| 16 | 4.69 | 4.08 | 3.73 | 3.50 | 3.34 | 3.22 | 3.12 | 3.05 | 2.99 | 2.89 | 2.79 | 2.68 | 2.57 | 2.45 | 2.32 | 16 |
| 17 | 4.62 | 4.01 | 3.66 | 3.44 | 3.28 | 3.16 | 3.06 | 2.98 | 2.92 | 2.82 | 2.72 | 2.62 | 2.50 | 2.38 | 2.25 | 17 |
| 18 | 4.56 | 3.95 | 3.61 | 3.38 | 3.22 | 3.10 | 3.00 | 2.93 | 2.87 | 2.77 | 2.67 | 2.56 | 2.44 | 2.32 | 2.19 | 18 |
| 19 | 4.51 | 3.90 | 3.56 | 3.33 | 3.17 | 3.05 | 2.96 | 2.88 | 2.82 | 2.72 | 2.62 | 2.51 | 2.39 | 2.27 | 2.13 | 19 |
| 20 | 4.46 | 3.86 | 3.51 | 3.29 | 3.13 | 3.01 | 2.91 | 2.84 | 2.77 | 2.68 | 2.57 | 2.46 | 2.35 | 2.22 | 2.08 | 20 |
| 21 | 4.42 | 3.82 | 3.47 | 3.25 | 3.09 | 2.97 | 2.87 | 2.80 | 2.73 | 2.64 | 2.53 | 2.42 | 2.31 | 2.18 | 2.04 | 21 |
| 22 | 4.38 | 3.73 | 3.44 | 3.21 | 3.05 | 2.93 | 2.84 | 2.76 | 2.70 | 2.60 | 2.50 | 2.39 | 2.27 | 2.14 | 2.00 | 22 |
| 23 | 4.35 | 3.75 | 3.41 | 3.18 | 3.02 | 2.90 | 2.81 | 2.73 | 2.67 | 2.57 | 2.47 | 2.36 | 2.24 | 2.11 | 1.97 | 23 |
| 24 | 4.32 | 3.72 | 3.38 | 3.15 | 2.99 | 2.87 | 2.78 | 2.70 | 2.64 | 2.54 | 2.44 | 2.33 | 2.21 | 2.08 | 1.93 | 24 |
| 25 | 4.29 | 3.69 | 3.35 | 3.13 | 2.97 | 2.85 | 2.75 | 2.68 | 2.61 | 2.51 | 2.41 | 2.30 | 2.18 | 2.05 | 1.91 | 25 |
| 26 | 4.26 | 3.67 | 3.33 | 3.10 | 2.94 | 2.82 | 2.73 | 2.65 | 2.59 | 2.49 | 2.39 | 2.28 | 2.16 | 2.03 | 1.88 | 26 |
| 27 | 4.24 | 3.65 | 3.31 | 3.08 | 2.92 | 2.80 | 2.71 | 2.63 | 2.57 | 2.47 | 2.36 | 2.25 | 2.13 | 2.00 | 1.85 | 27 |
| 28 | 4.22 | 3.63 | 3.29 | 3.06 | 2.90 | 2.78 | 2.69 | 2.61 | 2.55 | 2.45 | 2.34 | 2.23 | 2.11 | 1.98 | 1.83 | 28 |
| 29 | 4.20 | 3.61 | 3.27 | 3.04 | 2.88 | 2.76 | 2.67 | 2.59 | 2.53 | 2.43 | 2.32 | 2.21 | 2.09 | 1.96 | 1.81 | 29 |
| 30 | 4.18 | 3.59 | 3.25 | 3.03 | 2.87 | 2.75 | 2.65 | 2.57 | 2.51 | 2.41 | 2.31 | 2.19 | 2.07 | 1.94 | 1.79 | 30 |
| 31 | 4.16 | 3.57 | 3.23 | 3.01 | 2.85 | 2.73 | 2.63 | 2.56 | 2.49 | 2.40 | 2.29 | 2.18 | 2.06 | 1.92 | 1.77 | 31 |
| 32 | 4.15 | 3.56 | 3.22 | 2.99 | 2.84 | 2.71 | 2.62 | 2.54 | 2.48 | 2.38 | 2.27 | 2.16 | 2.04 | 1.90 | 1.75 | 32 |
| 33 | 4.13 | 3.54 | 3.20 | 2.98 | 2.82 | 2.70 | 2.61 | 2.53 | 2.47 | 2.37 | 2.26 | 2.15 | 2.03 | 1.89 | 1.73 | 33 |
| 34 | 4.12 | 3.53 | 3.19 | 2.97 | 2.81 | 2.69 | 2.59 | 2.52 | 2.45 | 2.35 | 2.25 | 2.13 | 2.01 | 1.87 | 1.72 | 34 |
| 35 | 4.11 | 3.52 | 3.18 | 2.96 | 2.80 | 2.68 | 2.58 | 2.50 | 2.44 | 2.34 | 2.23 | 2.12 | 2.00 | 1.86 | 1.70 | 35 |
| 36 | 4.09 | 3.50 | 3.17 | 2.94 | 2.78 | 2.66 | 2.57 | 2.49 | 2.43 | 2.33 | 2.22 | 2.11 | 1.99 | 1.85 | 1.69 | 36 |
| 37 | 4.08 | 3.49 | 3.16 | 2.93 | 2.77 | 2.65 | 2.56 | 2.48 | 2.42 | 2.32 | 2.21 | 2.10 | 1.97 | 1.84 | 1.67 | 37 |
| 38 | 4.07 | 3.48 | 3.14 | 2.92 | 2.76 | 2.64 | 2.55 | 2.47 | 2.41 | 2.31 | 2.20 | 2.09 | 1.96 | 1.82 | 1.66 | 38 |
| 39 | 4.06 | 3.47 | 3.13 | 2.91 | 2.75 | 2.63 | 2.54 | 2.46 | 2.40 | 2.30 | 2.19 | 2.08 | 1.95 | 1.81 | 1.65 | 39 |
| 40 | 4.05 | 3.46 | 3.13 | 2.90 | 2.74 | 2.62 | 2.53 | 2.45 | 2.39 | 2.29 | 2.18 | 2.07 | 1.94 | 1.80 | 1.64 | 40 |
| 42 | 4.03 | 3.45 | 3.11 | 2.89 | 2.73 | 2.61 | 2.51 | 2.43 | 2.37 | 2.27 | 2.16 | 2.05 | 1.92 | 1.78 | 1.61 | 42 |
| 44 | 4.02 | 3.43 | 3.09 | 2.87 | 2.71 | 2.59 | 2.50 | 2.42 | 2.35 | 2.25 | 2.15 | 2.03 | 1.91 | 1.77 | 1.60 | 44 |
| 46 | 4.00 | 3.41 | 3.08 | 2.86 | 2.70 | 2.58 | 2.48 | 2.40 | 2.34 | 2.24 | 2.13 | 2.02 | 1.89 | 1.75 | 1.58 | 46 |
| 48 | 3.99 | 3.40 | 3.07 | 2.84 | 2.68 | 2.56 | 2.47 | 2.39 | 2.33 | 2.23 | 2.12 | 2.01 | 1.88 | 1.73 | 1.56 | 48 |
| 50 | 3.97 | 3.39 | 3.05 | 2.83 | 2.67 | 2.56 | 2.46 | 2.38 | 2.32 | 2.22 | 2.11 | 1.99 | 1.87 | 1.72 | 1.54 | 50 |
| 60 | 3.92 | 3.34 | 3.01 | 2.79 | 2.63 | 2.51 | 2.41 | 2.33 | 2.27 | 2.17 | 2.06 | 1.94 | 1.81 | 1.67 | 1.48 | 60 |
| 80 | 3.86 | 3.28 | 2.95 | 2.73 | 2.57 | 2.45 | 2.35 | 2.28 | 2.21 | 2.11 | 2.00 | 1.88 | 1.75 | 1.60 | 1.40 | 80 |
| 120 | 3.80 | 3.23 | 2.89 | 2.67 | 2.51 | 2.39 | 2.30 | 2.22 | 2.16 | 2.05 | 1.94 | 1.82 | 1.69 | 1.53 | 1.31 | 120 |
| 240 | 3.75 | 3.17 | 2.84 | 2.62 | 2.46 | 2.34 | 2.24 | 2.17 | 2.10 | 2.00 | 1.89 | 1.77 | 1.63 | 1.46 | 1.20 | 240 |
| ∞ | 3.69 | 3.12 | 2.79 | 2.57 | 2.41 | 2.29 | 2.19 | 2.11 | 2.05 | 1.94 | 1.83 | 1.71 | 1.57 | 1.39 | 1.00 | ∞ |
附表8(1)F 值表(方差分析用)

P=0.05
| r2 | r1(较大均方的自由度) | r2 | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 16 | 18 | 20 | ||
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 241 | 242 | 244 | 245 | 246 | 247 | 248 | 1 |
| 2 | 18.5 | 19.0 | 19.2 | 19.2 | 19.3 | 19.3 | 19.4 | 19.4 | 19.4 | 19.4 | 19.4 | 19.4 | 19.4 | 19.4 | 19.4 | 2 |
| 3 | 10.1 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 | 8.81 | 8.79 | 8.74 | 8.71 | 8.69 | 8.67 | 8.66 | 3 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.91 | 5.87 | 5.84 | 5.82 | 5.80 | 4 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.77 | 4.74 | 4.68 | 4.64 | 4.60 | 4.58 | 4.56 | 5 |
| 6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 4.00 | 3.96 | 3.92 | 3.90 | 3.87 | 6 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.64 | 3.57 | 3.53 | 3.49 | 3.47 | 3.44 | 7 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.35 | 3.28 | 3.24 | 3.20 | 3.17 | 3.15 | 8 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.14 | 3.07 | 3.03 | 2.99 | 2.96 | 2.94 | 9 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.98 | 2.91 | 2.86 | 2.83 | 2.80 | 2.77 | 10 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.85 | 2.79 | 2.74 | 2.70 | 2.67 | 2.65 | 11 |
| 12 | 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.80 | 2.75 | 2.69 | 2.64 | 2.60 | 2.57 | 2.54 | 12 |
| 13 | 4.67 | 3.81 | 3.41 | 3.18 | 3.03 | 2.92 | 2.83 | 2.77 | 2.71 | 2.67 | 2.60 | 2.55 | 2.51 | 2.48 | 2.46 | 13 |
| 14 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.65 | 2.60 | 2.53 | 2.48 | 2.44 | 2.41 | 2.39 | 14 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.71 | 2.64 | 2.59 | 2.54 | 2.48 | 2.42 | 2.38 | 2.35 | 2.33 | 15 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.42 | 2.37 | 2.33 | 2.30 | 2.28 | 16 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.61 | 2.55 | 2.49 | 2.45 | 2.38 | 2.33 | 2.29 | 2.26 | 2.23 | 17 |
| 18 | 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.46 | 2.41 | 2.34 | 2.29 | 2.25 | 2.22 | 2.19 | 18 |
| 19 | 4.38 | 3.52 | 3.13 | 2.90 | 2.74 | 2.63 | 2.54 | 2.48 | 2.42 | 2.38 | 2.31 | 2.26 | 2.21 | 2.18 | 2.16 | 19 |
| 20 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.51 | 2.45 | 2.39 | 2.35 | 2.28 | 2.22 | 2.18 | 2.15 | 2.12 | 20 |
| 21 | 4.32 | 3.47 | 3.07 | 2.84 | 2.68 | 2.57 | 2.49 | 2.42 | 2.37 | 2.32 | 2.25 | 2.20 | 2.16 | 2.12 | 2.10 | 21 |
| 22 | 4.30 | 3.44 | 3.05 | 2.82 | 2.66 | 2.55 | 2.46 | 2.40 | 2.34 | 2.30 | 2.23 | 2.17 | 2.13 | 2.10 | 2.07 | 22 |
| 23 | 4.28 | 3.42 | 3.03 | 2.80 | 2.64 | 2.53 | 2.44 | 2.37 | 2.32 | 2.27 | 2.20 | 2.15 | 2.11 | 2.07 | 2.05 | 23 |
| 24 | 4.26 | 3.40 | 3.01 | 2.78 | 2.62 | 2.51 | 2.42 | 2.36 | 2.30 | 2.25 | 2.18 | 2.13 | 2.09 | 2.05 | 2.03 | 24 |
| 25 | 4.24 | 3.39 | 2.99 | 2.76 | 2.60 | 2.49 | 2.40 | 2.34 | 2.28 | 2.24 | 2.16 | 2.11 | 2.07 | 2.04 | 2.01 | 25 |
| 26 | 4.23 | 3.37 | 2.98 | 2.74 | 2.59 | 2.47 | 2.39 | 2.32 | 2.27 | 2.22 | 2.15 | 2.09 | 2.05 | 2.02 | 1.99 | 26 |
| 27 | 4.21 | 3.35 | 2.96 | 2.73 | 2.57 | 2.46 | 2.37 | 2.31 | 2.25 | 2.20 | 2.13 | 2.08 | 2.04 | 2.00 | 1.97 | 27 |
| 28 | 4.20 | 3.34 | 2.95 | 2.71 | 2.56 | 2.45 | 2.36 | 2.29 | 2.24 | 2.19 | 2.12 | 2.06 | 2.02 | 1.99 | 1.96 | 28 |
| 29 | 4.18 | 3.33 | 2.93 | 2.70 | 2.55 | 2.43 | 2.35 | 2.28 | 2.22 | 2.18 | 2.10 | 2.05 | 2.01 | 1.97 | 1.94 | 29 |
| 30 | 4.17 | 3.32 | 2.92 | 2.69 | 2.53 | 2.42 | 2.33 | 2.27 | 2.21 | 2.16 | 2.09 | 2.04 | 1.99 | 1.96 | 1.93 | 30 |
| 32 | 4.15 | 3.29 | 2.90 | 2.67 | 2.51 | 2.40 | 2.31 | 2.24 | 2.19 | 2.14 | 2.07 | 2.01 | 1.97 | 1.94 | 1.91 | 32 |
| 34 | 4.13 | 3.28 | 2.88 | 2.65 | 2.49 | 2.38 | 2.29 | 2.23 | 2.17 | 2.12 | 2.05 | 1.99 | 1.95 | 1.92 | 1.89 | 34 |
| 36 | 4.11 | 3.26 | 2.87 | 2.63 | 2.48 | 2.36 | 2.28 | 2.21 | 2.15 | 2.11 | 2.03 | 1.98 | 1.93 | 1.90 | 1.87 | 36 |
| 38 | 4.10 | 3.24 | 2.85 | 2.62 | 2.46 | 2.35 | 2.26 | 2.19 | 2.14 | 2.09 | 2.02 | 1.96 | 1.92 | 1.88 | 1.85 | 38 |
| 40 | 4.08 | 3.23 | 2.84 | 2.61 | 2.45 | 2.34 | 2.25 | 2.18 | 2.12 | 2.08 | 2.00 | 1.95 | 1.90 | 1.87 | 1.84 | 40 |
| 42 | 4.07 | 3.22 | 2.83 | 2.59 | 2.44 | 2.32 | 2.24 | 2.17 | 2.11 | 2.06 | 1.99 | 1.93 | 1.89 | 1.86 | 1.83 | 42 |
| 44 | 4.06 | 3.21 | 2.82 | 2.58 | 2.43 | 2.31 | 2.23 | 2.16 | 2.10 | 2.05 | 1.98 | 1.92 | 1.88 | 1.84 | 1.81 | 44 |
| 46 | 4.05 | 3.20 | 2.81 | 2.57 | 2.42 | 2.30 | 2.22 | 2.15 | 2.09 | 2.04 | 1.97 | 1.91 | 1.87 | 1.83 | 1.80 | 46 |
| 48 | 4.04 | 3.19 | 2.80 | 2.57 | 2.41 | 2.29 | 2.21 | 2.14 | 2.08 | 2.03 | 1.96 | 1.90 | 1.86 | 1.82 | 1.79 | 48 |
| 50 | 4.03 | 3.18 | 2.79 | 2.56 | 2.40 | 2.29 | 2.20 | 2.13 | 2.07 | 2.03 | 1.95 | 1.89 | 1.85 | 1.81 | 1.78 | 50 |
| 60 | 4.00 | 3.15 | 2.76 | 2.53 | 2.37 | 2.25 | 2.17 | 2.10 | 2.04 | 1.99 | 1.92 | 1.86 | 1.82 | 1.78 | 1.75 | 60 |
| 80 | 3.96 | 3.11 | 2.72 | 2.49 | 2.33 | 2.21 | 2.13 | 2.06 | 2.00 | 1.95 | 1.88 | 1.82 | 1.77 | 1.73 | 1.70 | 80 |
| 100 | 3.94 | 3.09 | 2.70 | 2.46 | 2.31 | 2.19 | 2.10 | 2.03 | 1.97 | 1.93 | 1.85 | 1.79 | 1.75 | 1.71 | 1.68 | 100 |
| 125 | 3.92 | 3.07 | 2.68 | 2.44 | 2.29 | 2.17 | 2.08 | 2.01 | 1.96 | 1.91 | 1.83 | 1.77 | 1.72 | 1.69 | 1.65 | 125 |
| 150 | 3.90 | 3.06 | 2.66 | 2.43 | 2.27 | 2.16 | 2.07 | 2.00 | 1.94 | 1.89 | 1.82 | 1.76 | 1.71 | 1.67 | 1.64 | 150 |
| 200 | 3.89 | 3.04 | 2.65 | 2.42 | 2.26 | 2.14 | 2.06 | 1.98 | 1.93 | 1.88 | 1.80 | 1.74 | 1.69 | 1.66 | 1.62 | 200 |
| 300 | 3.87 | 3.03 | 2.63 | 2.40 | 2.24 | 2.13 | 2.04 | 1.97 | 1.91 | 1.86 | 1.78 | 1.72 | 1.68 | 1.64 | 1.61 | 300 |
| 500 | 3.86 | 3.01 | 2.62 | 2.39 | 2.23 | 2.12 | 2.03 | 1.96 | 1.90 | 1.85 | 1.77 | 1.71 | 1.66 | 1.62 | 1.59 | 500 |
| 1000 | 3.85 | 3.00 | 2.61 | 2.38 | 2.22 | 2.11 | 2.02 | 1.95 | 1.89 | 1.84 | 1.76 | 1.70 | 1.65 | 1.61 | 1.58 | 1000 |
| ∞ | 3.84 | 3.00 | 2.60 | 2.37 | 2.21 | 2.10 | 2.01 | 1.94 | 1.88 | 1.83 | 1.75 | 1.69 | 1.64 | 1.60 | 1.57 | ∞ |
附表8(2) F 值表(方差分析用)
P=0.05
| n'2 | n'1(较大均方的自由度) | n'2 | ||||||||||||||
| 22 | 24 | 26 | 28 | 30 | 35 | 40 | 45 | 50 | 60 | 80 | 100 | 200 | 500 | 00 | ||
| 1 | 249 | 249 | 249 | 250 | 250 | 251 | 251 | 251 | 252 | 252 | 252 | 253 | 254 | 254 | 254 | 1 |
| 2 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 19.5 | 2 |
| 3 | 8.65 | 8.64 | 8.63 | 8.62 | 8.62 | 8.60 | 8.59 | 8.59 | 8.58 | 8.57 | 8.56 | 8.55 | 8.54 | 8.53 | 8.53 | 3 |
| 4 | 5.79 | 5.77 | 5.76 | 5.75 | 5.75 | 5.73 | 5.72 | 5.71 | 5.70 | 7.69 | 5.67 | 5.66 | 5.65 | 5.64 | 5.63 | 4 |
| 5 | 4.54 | 5.53 | 4.52 | 4.50 | 4.50 | 4.48 | 4.46 | 4.45 | 4.44 | 4.43 | 4.41 | 4.41 | 4.39 | 4.37 | 4.37 | 5 |
| 6 | 3.86 | 3.84 | 3.83 | 3.82 | 3.81 | 3.79 | 3.77 | 3.76 | 3.75 | 3.74 | 3.72 | 3.71 | 3.69 | 3.68 | 3.67 | 6 |
| 7 | 3.43 | 3.41 | 3.40 | 3.39 | 3.38 | 3.36 | 3.34 | 3.33 | 3.32 | 3.30 | 3.29 | 3.27 | 3.25 | 3.24 | 3.23 | 7 |
| 8 | 3.13 | 3.12 | 3.10 | 3.09 | 3.08 | 3.06 | 3.04 | 3.03 | 3.02 | 3.01 | 2.99 | 2.97 | 2.95 | 2.94 | 2.93 | 8 |
| 9 | 2.92 | 2.90 | 2.89 | 2.87 | 2.83 | 2.84 | 2.83 | 2.81 | 2.80 | 2.79 | 2.77 | 2.76 | 2.73 | 2.72 | 2.71 | 9 |
| 10 | 2.75 | 2.74 | 2.72 | 2.71 | 2.70 | 2.68 | 2.66 | 2.65 | 2.64 | 2.62 | 2.60 | 2.59 | 2.56 | 2.55 | 0.54 | 10 |
| 11 | 2.63 | 2.61 | 2.59 | 2.58 | 2.57 | 2.55 | 2.53 | 2.52 | 2.51 | 2.49 | 2.47 | 2.46 | 2.43 | 2.42 | 2.40 | 11 |
| 12 | 2.52 | 2.51 | 2.49 | 2.48 | 2.47 | 2.44 | 2.43 | 2.41 | 2.40 | 2.38 | 2.36 | 2.35 | 2.32 | 2.31 | 2.30 | 12 |
| 13 | 2.44 | 2.42 | 2.41 | 2.39 | 2.38 | 2.36 | 2.34 | 2.33 | 2.31 | 2.30 | 2.27 | 2.26 | 2.23 | 2.22 | 2.21 | 13 |
| 14 | 2.37 | 2.35 | 2.33 | 2.32 | 2.31 | 2.28 | 2.27 | 2.25 | 2.24 | 2.22 | 2.20 | 2.19 | 2.16 | 2.14 | 2.13 | 14 |
| 15 | 2.31 | 2.29 | 2.27 | 2.26 | 2.25 | 2.22 | 2.20 | 2.19 | 2.18 | 2.16 | 2.14 | 2.12 | 2.10 | 2.08 | 2.07 | 15 |
| 16 | 2.25 | 2.24 | 2.22 | 2.21 | 2.19 | 2.17 | 2.15 | 2.14 | 2.12 | 2.11 | 2.08 | 2.07 | 2.04 | 2.02 | 2.01 | 16 |
| 17 | 2.21 | 2.19 | 2.17 | 2.16 | 2.15 | 2.12 | 2.10 | 2.09 | 2.08 | 2.06 | 2.03 | 2.02 | 1.99 | 1.97 | 1.96 | 17 |
| 18 | 2.17 | 2.15 | 2.13 | 2.12 | 2.11 | 2.08 | 2.06 | 2.05 | 2.04 | 2.02 | 1.99 | 1.98 | 1.95 | 1.93 | 1.92 | 18 |
| 19 | 2.13 | 2.11 | 2.10 | 2.08 | 2.07 | 2.05 | 2.03 | 2.01 | 2.00 | 1.98 | 1.96 | 1.94 | 1.91 | 1.89 | 1.88 | 19 |
| 20 | 2.10 | 2.08 | 2.07 | 2.05 | 2.04 | 2.01 | 1.99 | 1.98 | 1.97 | 1.95 | 1.92 | 1.91 | 1.88 | 1.86 | 1.84 | 20 |
| 21 | 2.07 | 2.05 | 2.04 | 2.02 | 2.01 | 1.98 | 1.96 | 1.95 | 1.94 | 1.92 | 1.89 | 1.88 | 1.84 | 1.82 | 1.81 | 21 |
| 22 | 2.05 | 2.03 | 2.01 | 2.00 | 1.98 | 1.96 | 1.94 | 1.92 | 1.91 | 1.89 | 1.86 | 1.85 | 1.82 | 1.80 | 1.78 | 22 |
| 23 | 2.02 | 2.00 | 1.99 | 1.97 | 1.96 | 1.93 | 1.91 | 1.90 | 1.88 | 1.86 | 1.84 | 1.82 | 1.79 | 1.77 | 1.76 | 23 |
| 24 | 2.00 | 1.98 | 1.97 | 1.95 | 1.94 | 1.91 | 1.89 | 1.88 | 1.86 | 1.84 | 1.82 | 1.80 | 1.77 | 1.75 | 1.73 | 34 |
| 25 | 1.98 | 1.96 | 1.95 | 1.93 | 1.92 | 1.89 | 1.87 | 1.86 | 1.84 | 1.82 | 1.80 | 1.78 | 1.75 | 1.73 | 1.71 | 25 |
| 26 | 1.97 | 1.95 | 1.93 | 1.91 | 1.90 | 1.87 | 1.85 | 1.84 | 1.82 | 1.80 | 1.78 | 1.76 | 1.73 | 1.71 | 1.69 | 26 |
| 27 | 1.95 | 1.93 | 1.91 | 1.90 | 1.88 | 1.86 | 1.84 | 1.82 | 1.81 | 1.79 | 1.76 | 1.74 | 1.71 | 1.69 | 1.67 | 27 |
| 28 | 1.93 | 1.91 | 1.90 | 1.88 | 1.87 | 1.84 | 1.82 | 1.80 | 1.79 | 1.77 | 1.74 | 1.73 | 1.69 | 1.67 | 1.65 | 28 |
| 29 | 1.92 | 1.90 | 1.88 | 1.87 | 1.85 | 1.83 | 1.81 | 1.79 | 1.77 | 1.75 | 1.73 | 1.71 | 1.67 | 1.65 | 1.64 | 29 |
| 30 | 1.91 | 1.89 | 1.87 | 1.85 | 1.84 | 1.81 | 1.79 | 1.77 | 1.76 | 1.74 | 1.71 | 1.70 | 1.66 | 1.64 | 1.62 | 30 |
| 32 | 1.88 | 1.86 | 1.85 | 1.83 | 1.82 | 1.79 | 1.77 | 1.75 | 1.74 | 1.71 | 1.69 | 1.67 | 1.63 | 1.61 | 1.59 | 32 |
| 34 | 1.86 | 1.84 | 1.82 | 1.80 | 1.80 | 1.77 | 1.75 | 1.73 | 1.71 | 1.69 | 1.66 | 1.65 | 1.61 | 1.59 | 1.57 | 34 |
| 36 | 1.85 | 1.82 | 1.81 | 1.79 | 1.78 | 1.75 | 1.73 | 1.71 | 1.69 | 1.67 | 1.64 | 1.62 | 1.59 | 1.56 | 1.55 | 36 |
| 38 | 1.83 | 1.81 | 1.79 | 1.77 | 1.76 | 1.73 | 1.71 | 1.69 | 1.68 | 1.65 | 1.62 | 1.61 | 1.57 | 1.54 | 1.53 | 38 |
| 40 | 1.81 | 1.79 | 1.77 | 1.76 | 1.74 | 1.72 | 1.69 | 1.67 | 1.66 | 1.64 | 1.61 | 1.59 | 1.55 | 1.53 | 1.51 | 40 |
| 42 | 1.80 | 1.78 | 1.76 | 1.74 | 1.73 | 1.70 | 1.68 | 1.66 | 1.65 | 1.62 | 1.59 | 1.57 | 1.53 | 1.51 | 1.49 | 42 |
| 44 | 1.79 | 1.77 | 1.75 | 1.73 | 1.72 | 1.69 | 1.67 | 1.65 | 1.63 | 1.61 | 1.58 | 1.56 | 1.52 | 1.49 | 1.48 | 44 |
| 46 | 1.78 | 1.76 | 1.74 | 1.72 | 1.71 | 1.68 | 1.65 | 1.64 | 1.62 | 1.60 | 1.57 | 1.55 | 1.51 | 1.48 | 1.46 | 46 |
| 48 | 1.77 | 1.75 | 1.73 | 1.71 | 1.70 | 1.67 | 1.64 | 1.62 | 1.61 | 1.59 | 1.56 | 1.54 | 1.49 | 1.47 | 1.45 | 48 |
| 50 | 1.76 | 1.74 | 1.72 | 1.70 | 1.69 | 1.66 | 1.63 | 1.61 | 1.60 | 1.58 | 1.54 | 1.52 | 1.48 | 1.46 | 1.44 | 50 |
| 60 | 1.72 | 1.70 | 1.68 | 1.66 | 1.65 | 1.62 | 1.59 | 1.57 | 1.56 | 1.53 | 1.50 | 1.48 | 1.44 | 1.41 | 1.39 | 60 |
| 80 | 1.68 | 1.65 | 1.63 | 1.62 | 1.60 | 1.57 | 1.54 | 1.52 | 1.51 | 1.48 | 1.45 | 1.43 | 1.38 | 1.35 | 1.32 | 80 |
| 100 | 1.65 | 1.63 | 1.61 | 1.59 | 1.57 | 1.54 | 1.52 | 1.49 | 1.48 | 1.45 | 1.41 | 1.39 | 1.34 | 1.31 | 1.28 | 100 |
| 125 | 1.63 | 1.60 | 1.58 | 1.57 | 1.55 | 1.52 | 1.49 | 1.47 | 1.45 | 1.42 | 1.39 | 1.36 | 1.31 | 1.27 | 1.25 | 125 |
| 150 | 1.61 | 1.59 | 1.57 | 1.55 | 1.53 | 1.50 | 1.48 | 1.45 | 1.44 | 1.41 | 1.37 | 1.34 | 1.29 | 1.25 | 1.22 | 150 |
| 200 | 1.60 | 1.57 | 1.55 | 1.53 | 1.52 | 1.48 | 1.46 | 1.43 | 1.41 | 1.39 | 1.35 | 1.32 | 1.26 | 1.22 | 1.19 | 200 |
| 300 | 1.58 | 1.55 | 1.53 | 1.51 | 1.50 | 1.46 | 1.43 | 1.41 | 1.39 | 1.36 | 1.32 | 1.30 | 1.23 | 1.19 | 1.15 | 300 |
| 500 | 1.56 | 1.54 | 1.52 | 1.50 | 1.48 | 1.45 | 1.42 | 1.40 | 1.38 | 1.34 | 1.30 | 1.28 | 1.21 | 1.16 | 1.11 | 500 |
| 1000 | 1.55 | 1.53 | 1.51 | 1.49 | 1.47 | 1.44 | 1.41 | 1.38 | 1.36 | 1.33 | 1.29 | 1.26 | 1.19 | 1.13 | 1.08 | 1000 |
| ∞ | 1.54 | 1.52 | 1.50 | 1.48 | 1.46 | 1.42 | 1.39 | 1.37 | 1.35 | 1.32 | 1.27 | 1.24 | 1.17 | 1.11 | 1.00 | ∞ |
附表8(3) F 值表(方差分析用)

P=0.01
| nˊ2 | nˊ1(较大均方的自由度) | nˊ2 | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 16 | 18 | 20 | ||
| 1 | 4052 | 5000 | 5403 | 5625 | 5754 | 5859 | 5928 | 5981 | 6022 | 6056 | 6106 | 6142 | 6169 | 6190 | 6209 | 1 |
| 2 | 98.5 | 99.0 | 99.2 | 99.2 | 99.3 | 99.3 | 99.4 | 99.4 | 99.4 | 99.4 | 99.4 | 99.4 | 99.4 | 99.4 | 99.4 | 2 |
| 3 | 34.1 | 30.8 | 29.5 | 28.7 | 28.2 | 27.9 | 27.7 | 27.5 | 27.3 | 27.2 | 27.1 | 26.9 | 26.8 | 26.8 | 26.7 | 3 |
| 4 | 21.2 | 18.0 | 16.7 | 16.0 | 15.5 | 15.2 | 15.0 | 14.8 | 14.7 | 14.5 | 14.4 | 14.2 | 14.2 | 14.1 | 14.0 | 4 |
| 5 | 16.3 | 13.3 | 12.1 | 11.4 | 11.0 | 10.7 | 10.5 | 10.3 | 10.2 | 10.1 | 9.89 | 9.77 | 9.68 | 9.61 | 9.55 | 5 |
| 6 | 13.7 | 10.9 | 9.78 | 9.15 | 8.75 | 8.47 | 8.26 | 8.10 | 7.98 | 7.87 | 7.72 | 7.60 | 7.52 | 7.45 | 7.40 | 6 |
| 7 | 12.2 | 9.55 | 8.45 | 7.85 | 7.46 | 7.19 | 6.99 | 6.84 | 6.72 | 6.62 | 6.47 | 6.36 | 6.27 | 6.21 | 6.16 | 7 |
| 8 | 11.3 | 8.65 | 7.59 | 7.01 | 6.63 | 6.37 | 6.18 | 6.03 | 5.91 | 5.81 | 5.67 | 5.56 | 5.48 | 5.41 | 5.36 | 8 |
| 9 | 10.6 | 8.02 | 6.99 | 6.42 | 6.06 | 5.80 | 5.61 | 5.47 | 5.35 | 5.26 | 5.11 | 5.00 | 4.92 | 4.86 | 4.81 | 9 |
| 10 | 10.0 | 7.56 | 6.55 | 5.99 | 5.64 | 5.39 | 5.20 | 5.06 | 4.94 | 4.85 | 4.71 | 4.60 | 4.52 | 4.46 | 4.41 | 10 |
| 11 | 9.65 | 7.21 | 6.22 | 5.67 | 5.32 | 5.07 | 4.89 | 4.74 | 4.63 | 4.54 | 4.40 | 4.29 | 4.21 | 4.15 | 4.10 | 11 |
| 12 | 9.33 | 6.93 | 5.95 | 5.41 | 5.06 | 4.82 | 4.64 | 4.50 | 4.39 | 4.30 | 4.16 | 4.05 | 3.97 | 3.91 | 3.86 | 12 |
| 13 | 9.07 | 6.70 | 5.74 | 5.21 | 4.86 | 4.62 | 4.44 | 4.30 | 4.19 | 4.10 | 2.96 | 3.86 | 3.73 | 3.71 | 3.66 | 13 |
| 14 | 8.86 | 6.51 | 5.56 | 5.04 | 4.70 | 4.46 | 4.23 | 4.14 | 4.03 | 3.94 | 3.80 | 3.70 | 3.62 | 3.56 | 3.51 | 14 |
| 15 | 8.68 | 6.36 | 5.42 | 4.89 | 4.56 | 4.32 | 4.14 | 4.00 | 3.89 | 3.80 | 3.67 | 3.56 | 3.49 | 3.42 | 3.37 | 15 |
| 16 | 8.53 | 6.23 | 5.29 | 4.77 | 4.44 | 4.20 | 4.03 | 3.89 | 3.78 | 3.69 | 3.55 | 3.45 | 3.37 | 3.31 | 3.26 | 16 |
| 17 | 8.40 | 6.11 | 5.18 | 4.67 | 4.34 | 4.10 | 3.93 | 3.79 | 3.68 | 3.59 | 3.46 | 3.35 | 3.27 | 3.21 | 3.16 | 17 |
| 18 | 8.29 | 6.01 | 5.39 | 4.58 | 4.25 | 4.01 | 3.84 | 3.71 | 3.60 | 3.51 | 3.37 | 3.27 | 3.19 | 3.13 | 3.68 | 18 |
| 19 | 8.18 | 5.93 | 5.01 | 4.50 | 4.17 | 3.94 | 3.77 | 3.63 | 3.52 | 3.43 | 3.30 | 3.10 | 3.12 | 3.05 | 3.00 | 19 |
| 20 | 8.10 | 5.85 | 4.94 | 4.43 | 4.10 | 3.37 | 3.70 | 3.56 | 3.46 | 3.37 | 3.23 | 3.13 | 3.05 | 2.99 | 2.94 | 20 |
| 21 | 8.02 | 5.78 | 4.87 | 4.37 | 4.04 | 3.81 | 3.64 | 3.51 | 3.40 | 3.31 | 3.17 | 3.07 | 2.99 | 2.93 | 2.88 | 21 |
| 22 | 7.95 | 5.72 | 4.82 | 4.31 | 3.99 | 3.76 | 3.59 | 3.45 | 3.35 | 3.26 | 3.12 | 3.02 | 2.94 | 2.88 | 2.83 | 22 |
| 23 | 7.88 | 5.66 | 4.76 | 4.26 | 3.94 | 3.71 | 3.54 | 3.41 | 3.30 | 3.21 | 3.07 | 2.97 | 2.89 | 2.83 | 2.78 | 23 |
| 24 | 7.82 | 5.61 | 4.72 | 4.22 | 3.90 | 3.67 | 3.50 | 3.36 | 3.26 | 3.17 | 3.03 | 2.93 | 2.85 | 2.79 | 2.74 | 24 |
| 25 | 7.77 | 5.57 | 4.68 | 4.18 | 3.86 | 3.63 | 3.46 | 3.32 | 3.22 | 3.13 | 2.99 | 2.89 | 2.81 | 2.75 | 2.70 | 25 |
| 26 | 7.72 | 5.53 | 4.64 | 4.14 | 3.82 | 3.59 | 3.42 | 3.29 | 3.18 | 3.09 | 2.96 | 2.86 | 2.78 | 2.72 | 2.66 | 26 |
| 27 | 7.68 | 5.49 | 4.60 | 4.11 | 3.78 | 3.56 | 3.39 | 3.26 | 3.15 | 3.06 | 2.93 | 2.82 | 2.75 | 2.68 | 2.63 | 27 |
| 28 | 7.64 | 5.45 | 4.57 | 4.07 | 3.75 | 3.53 | 3.36 | 3.23 | 3.12 | 3.03 | 2.90 | 2.79 | 2.72 | 2.65 | 2.60 | 28 |
| 29 | 7.60 | 5.42 | 4.54 | 4.04 | 3.73 | 3.50 | 3.33 | 3.20 | 3.09 | 3.00 | 2.87 | 2.77 | 2.69 | 2.62 | 2.57 | 29 |
| 30 | 7.56 | 5.39 | 4.51 | 4.02 | 3.70 | 3.47 | 3.30 | 3.17 | 3.07 | 2.98 | 2.84 | 2.74 | 2.66 | 2.60 | 2.55 | 30 |
| 32 | 7.50 | 5.34 | 4.46 | 3.07 | 3.65 | 3.43 | 3.26 | 3.13 | 3.02 | 2.93 | 2.80 | 2.70 | 2.62 | 2.55 | 2.50 | 32 |
| 34 | 7.44 | 5.29 | 4.42 | 3.93 | 3.61 | 3.39 | 3.22 | 3.09 | 2.98 | 2.89 | 2.76 | 2.66 | 2.58 | 2.51 | 2.46 | 34 |
| 36 | 7.40 | 5.25 | 4.38 | 3.89 | 3.57 | 3.35 | 3.18 | 3.05 | 2.95 | 2.86 | 2.72 | 2.62 | 2.54 | 2.48 | 2.43 | 36 |
| 38 | 7.35 | 5.21 | 4.34 | 3.86 | 3.54 | 3.32 | 3.15 | 3.02 | 2.92 | 2.83 | 2.69 | 2.59 | 2.51 | 2.45 | 2.40 | 38 |
| 40 | 7.31 | 5.18 | 4.31 | 3.83 | 3.51 | 3.29 | 3.12 | 2.99 | 2.89 | 2.80 | 2.66 | 2.56 | 2.48 | 2.42 | 2.37 | 40 |
| 42 | 7.28 | 5.15 | 4.29 | 3.80 | 3.49 | 3.27 | 3.10 | 2.97 | 2.86 | 2.78 | 2.64 | 2.54 | 2.46 | 2.40 | 2.34 | 42 |
| 44 | 7.25 | 5.12 | 4.26 | 3.78 | 3.47 | 3.24 | 3.08 | 2.95 | 2.84 | 2.75 | 2.62 | 2.52 | 2.44 | 2.37 | 2.32 | 44 |
| 46 | 7.22 | 5.10 | 4.24 | 3.76 | 3.44 | 3.22 | 3.06 | 2.93 | 2.82 | 2.73 | 2.60 | 2.50 | 2.42 | 2.35 | 2.30 | 46 |
| 48 | 7.20 | 5.08 | 4.22 | 3.74 | 3.43 | 3.20 | 3.04 | 2.91 | 2.80 | 2.72 | 2.58 | 2.48 | 2.40 | 2.33 | 2.28 | 48 |
| 50 | 7.17 | 5.06 | 4.20 | 3.72 | 3.41 | 3.19 | 3.02 | 2.89 | 2.79 | 2.70 | 2.56 | 2.46 | 2.38 | 2.32 | 2.27 | 50 |
| 60 | 7.08 | 4.98 | 4.13 | 3.65 | 3.34 | 3.12 | 2.95 | 2.82 | 2.72 | 2.63 | 2.59 | 2.39 | 2.31 | 2.25 | 2.20 | 60 |
| 80 | 6.96 | 4.88 | 4.04 | 3.56 | 3.26 | 3.04 | 2.87 | 2.74 | 2.64 | 2.55 | 2.42 | 2.31 | 2.23 | 2.17 | 2.12 | 80 |
| 100 | 6.90 | 4.82 | 3.98 | 3.51 | 3.21 | 2.99 | 2.82 | 2.69 | 2.59 | 2.50 | 2.37 | 2.26 | 2.19 | 2.12 | 2.07 | 100 |
| 125 | 6.84 | 4.78 | 3.94 | 3.47 | 3.17 | 2.95 | 2.79 | 2.66 | 2.55 | 2.47 | 2.33 | 2.23 | 2.15 | 2.08 | 2.03 | 125 |
| 150 | 6.81 | 4.75 | 3.92 | 3.45 | 3.14 | 2.92 | 2.76 | 2.63 | 2.53 | 2.44 | 2.31 | 2.20 | 2.12 | 2.06 | 2.00 | 150 |
| 200 | 6.76 | 4.71 | 3.88 | 3.41 | 3.11 | 2.89 | 2.73 | 2.60 | 2.50 | 2.41 | 2.27 | 2.17 | 2.09 | 2.02 | 1.97 | 200 |
| 300 | 6.72 | 4.68 | 3.85 | 3.38 | 3.08 | 2.86 | 2.70 | 2.57 | 2.47 | 2.38 | 2.24 | 2.14 | 2.06 | 1.99 | 1.94 | 300 |
| 500 | 6.69 | 4.65 | 3.82 | 3.36 | 3.05 | 2.84 | 2.68 | 2.55 | 2.44 | 2.36 | 2.22 | 2.12 | 2.04 | 1.97 | 1.92 | 500 |
| 1000 | 6.66 | 4.63 | 3.80 | 3.34 | 3.04 | 2.82 | 2.66 | 2.53 | 2.43 | 2.34 | 2.20 | 2.10 | 2.02 | 1.95 | 1.90 | 1000 |
| ∞ | 6.63 | 4.61 | 3.78 | 3.32 | 3.02 | 2.80 | 2.64 | 2.51 | 2.41 | 2.32 | 2.18 | 2.08 | 2.00 | 1.93 | 1.88 | ∞ |
附表8(4)F 值表(方差分析用)
P=0.01
| nˊ2 | n'2(较大均方的自由度) | nˊ2 | ||||||||||||||
| 22 | 24 | 26 | 28 | 30 | 35 | 40 | 45 | 50 | 60 | 80 | 100 | 200 | 500 | ∞ | ||
| 1 | 6220 | 6234 | 6240 | 6250 | 6258 | 6280 | 6286 | 6300 | 6302 | 6310 | 6334 | 6330 | 6352 | 6361 | 6366 | 1 |
| 2 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 99.5 | 2 |
| 3 | 26.6 | 26.6 | 26.6 | 26.5 | 26.5 | 26.5 | 26.4 | 26.4 | 26.4 | 26.3 | 26.3 | 26.2 | 26.2 | 26.1 | 26.1 | 3 |
| 4 | 14.0 | 13.9 | 13.9 | 13.9 | 13.8 | 13.8 | 13.7 | 13.7 | 13.7 | 13.7 | 13.6 | 13.6 | 13.5 | 13.5 | 13.5 | 4 |
| 5 | 9.51 | 9.47 | 9.43 | 9.40 | 9.38 | 9.33 | 9.29 | 9.26 | 9.24 | 9.20 | 9.16 | 9.13 | 9.08 | 9.04 | 9.02 | 5 |
| 6 | 7.35 | 7.31 | 7.28 | 7.25 | 7.23 | 7.18 | 7.14 | 7.11 | 7.09 | 7.06 | 7.01 | 6.99 | 6.93 | 6.90 | 6.88 | 6 |
| 7 | 6.11 | 6.07 | 6.04 | 6.02 | 5.99 | 5.94 | 5.91 | 5.88 | 5.86 | 5.82 | 5.78 | 5.75 | 5.70 | 5.67 | 5.65 | 7 |
| 8 | 5.32 | 5.28 | 5.25 | 5.22 | 5.20 | 5.15 | 5.12 | 5.00 | 5.07 | 5.03 | 4.99 | 4.96 | 4.91 | 4.88 | 4.86 | 8 |
| 9 | 4.77 | 4.73 | 4.70 | 4.67 | 4.65 | 4.60 | 4.57 | 4.54 | 4.52 | 4.48 | 4.44 | 4.42 | 4.36 | 4.33 | 4.31 | 9 |
| 10 | 4.36 | 4.33 | 4.30 | 4.27 | 4.25 | 4.20 | 4.17 | 4.14 | 4.12 | 4.08 | 4.04 | 4.01 | 3.96 | 3.93 | 3.91 | 10 |
| 11 | 4.06 | 4.02 | 5.99 | 3.96 | 3.94 | 3.89 | 3.86 | 3.83 | 3.81 | 3.78 | 3.73 | 3.71 | 3.66 | 3.62 | 3.60 | 11 |
| 12 | 3.82 | 3.78 | 3.75 | 3.72 | 3.70 | 3.65 | 3.62 | 3.59 | 3.57 | 3.54 | 3.49 | 3.47 | 3.41 | 3.38 | 3.36 | 12 |
| 13 | 3.62 | 3.59 | 3.56 | 3.53 | 3.51 | 3.46 | 3.43 | 3.40 | 3.38 | 3.34 | 3.30 | 3.27 | 3.22 | 3.19 | 3.17 | 13 |
| 14 | 3.46 | 3.43 | 2.40 | 3.37 | 3.35 | 3.30 | 3.27 | 3.24 | 3.22 | 3.18 | 3.14 | 3.11 | 3.06 | 3.03 | 3.00 | 14 |
| 15 | 3.33 | 3.29 | 3.26 | 3.24 | 3.21 | 3.17 | 3.13 | 3.10 | 3.08 | 3.05 | 3.00 | 2.98 | 2.92 | 2.89 | 2.87 | 15 |
| 16 | 3.22 | 3.18 | 3.15 | 3.12 | 3.10 | 3.05 | 3.02 | 2.99 | 2.97 | 2.93 | 2.89 | 2.86 | 2.81 | 2.78 | 2.75 | 16 |
| 17 | 3.12 | 3.08 | 3.05 | 3.03 | 3.00 | 2.96 | 2.92 | 2.89 | 2.87 | 2.83 | 2.79 | 2.76 | 2.71 | 2.68 | 2.65 | 17 |
| 18 | 3.03 | 3.00 | 2.97 | 2.94 | 2.92 | 2.87 | 2.84 | 2.81 | 2.78 | 2.75 | 2.70 | 2.68 | 2.62 | 2.59 | 2.57 | 18 |
| 19 | 2.96 | 2.92 | 2.89 | 2.87 | 2.84 | 2.80 | 2.76 | 2.73 | 2.71 | 2.67 | 2.63 | 2.60 | 2.55 | 2.51 | 2.49 | 19 |
| 20 | 2.90 | 2.86 | 2.83 | 2.80 | 2.78 | 2.73 | 2.69 | 2.67 | 2.64 | 2.61 | 2.56 | 2.54 | 2.48 | 2.44 | 2.42 | 20 |
| 21 | 2.84 | 2.80 | 2.77 | 2.74 | 2.72 | 2.67 | 2.64 | 2.61 | 2.58 | 2.55 | 2.50 | 2.48 | 2.42 | 2.38 | 2.36 | 21 |
| 22 | 2.78 | 2.75 | 2.72 | 2.69 | 2.67 | 2.62 | 2.58 | 2.55 | 2.53 | 2.50 | 2.45 | 2.42 | 2.36 | 2.33 | 2.31 | 22 |
| 23 | 2.74 | 2.70 | 2.67 | 2.64 | 2.62 | 2.57 | 2.54 | 2.51 | 2.48 | 2.45 | 2.40 | 2.37 | 2.32 | 2.28 | 2.26 | 23 |
| 24 | 2.70 | 2.66 | 2.63 | 2.60 | 2.58 | 2.53 | 2.49 | 2.46 | 2.44 | 2.40 | 2.36 | 2.33 | 2.27 | 2.24 | 2.21 | 24 |
| 25 | 2.66 | 2.62 | 2.59 | 2.56 | 2.54 | 2.49 | 2.45 | 2.42 | 2.40 | 2.36 | 2.32 | 2.29 | 2.23 | 2.19 | 2.17 | 25 |
| 26 | 2.62 | 2.58 | 2.55 | 2.53 | 2.50 | 2.45 | 2.42 | 2.39 | 2.36 | 2.33 | 2.28 | 2.25 | 2.19 | 2.16 | 2.13 | 26 |
| 27 | 2.59 | 2.55 | 2.52 | 2.49 | 2.47 | 2.42 | 2.38 | 2.35 | 2.33 | 2.29 | 2.25 | 2.22 | 2.16 | 2.12 | 2.10 | 27 |
| 28 | 2.56 | 2.52 | 2.49 | 2.46 | 2.44 | 2.39 | 2.35 | 2.32 | 2.30 | 2.26 | 2.22 | 2.19 | 2.13 | 2.09 | 2.06 | 28 |
| 29 | 2.53 | 2.49 | 2.46 | 2.44 | 2.41 | 2.36 | 2.33 | 2.30 | 2.27 | 2.23 | 2.19 | 2.16 | 2.10 | 2.06 | 2.03 | 29 |
| 30 | 2.51 | 2.47 | 2.44 | 2.41 | 2.39 | 2.34 | 2.30 | 2.27 | 2.25 | 2.21 | 2.16 | 2.13 | 2.07 | 2.03 | 2.01 | 30 |
| 32 | 2.46 | 2.42 | 2.39 | 2.36 | 2.34 | 2.29 | 2.25 | 2.22 | 2.20 | 2.16 | 2.11 | 2.08 | 2.02 | 1.98 | 1.96 | 32 |
| 34 | 2.42 | 2.38 | 2.35 | 2.32 | 2.30 | 2.25 | 2.21 | 2.18 | 2.16 | 2.12 | 2.07 | 2.04 | 1.98 | 1.94 | 1.91 | 34 |
| 36 | 2.38 | 2.35 | 2.32 | 2.29 | 2.26 | 2.21 | 2.17 | 2.14 | 2.12 | 2.08 | 2.03 | 2.00 | 1.94 | 1.90 | 1.87 | 36 |
| 38 | 2.35 | 2.32 | 2.28 | 2.26 | 2.23 | 2.18 | 2.14 | 2.11 | 2.09 | 2.05 | 2.00 | 1.97 | 1.90 | 1.86 | 1.84 | 38 |
| 40 | 2.33 | 2.29 | 2.26 | 2.23 | 2.20 | 2.15 | 2.11 | 2.08 | 2.06 | 2.02 | 1.97 | 1.94 | 1.87 | 1.83 | 1.80 | 40 |
| 42 | 2.30 | 2.26 | 2.23 | 2.20 | 2.18 | 2.13 | 2.09 | 2.06 | 2.03 | 1.99 | 1.94 | 1.91 | 1.85 | 1.80 | 1.78 | 42 |
| 44 | 2.28 | 2.24 | 2.21 | 2.18 | 2.15 | 2.10 | 2.06 | 2.03 | 2.01 | 1.97 | 1.92 | 1.89 | 1.82 | 1.78 | 1.75 | 44 |
| 46 | 2.26 | 2.22 | 2.19 | 2.16 | 2.13 | 2.08 | 2.04 | 2.01 | 1.99 | 1.95 | 1.90 | 1.86 | 1.80 | 1.75 | 1.73 | 46 |
| 48 | 2.24 | 2.20 | 2.17 | 2.14 | 2.12 | 2.06 | 2.02 | 1.99 | 1.97 | 1.93 | 1.88 | 1.84 | 1.78 | 1.73 | 1.70 | 48 |
| 50 | 2.22 | 2.18 | 2.15 | 2.12 | 2.10 | 2.05 | 2.01 | 1.97 | 1.95 | 1.91 | 1.86 | 1.82 | 1.76 | 1.71 | 1.68 | 50 |
| 60 | 2.15 | 2.12 | 2.08 | 2.05 | 2.03 | 1.98 | 1.94 | 1.90 | 1.88 | 1.84 | 1.78 | 1.75 | 1.68 | 1.63 | 1.60 | 60 |
| 80 | 2.07 | 2.03 | 2.00 | 1.97 | 1.94 | 1.89 | 1.85 | 1.81 | 1.79 | 1.75 | 1.69 | 1.66 | 1.58 | 1.53 | 1.49 | 80 |
| 100 | 2.02 | 1.98 | 1.94 | 1.92 | 1.89 | 1.84 | 1.80 | 1.76 | 1.73 | 1.69 | 1.63 | 1.60 | 1.52 | 1.47 | 1.43 | 100 |
| 125 | 1.98 | 1.94 | 1.91 | 1.88 | 1.85 | 1.80 | 1.76 | 1.72 | 1.69 | 1.65 | 1.59 | 1.55 | 1.47 | 1.41 | 1.37 | 125 |
| 150 | 1.96 | 1.92 | 1.88 | 1.85 | 1.83 | 1.77 | 1.73 | 1.69 | 1.66 | 1.62 | 1.56 | 1.52 | 1.43 | 1.38 | 1.33 | 150 |
| 200 | 1.93 | 1.89 | 1.85 | 1.82 | 1.79 | 1.74 | 1.69 | 1.66 | 1.63 | 1.58 | 1.52 | 1.48 | 1.39 | 1.33 | 1.28 | 200 |
| 300 | 1.89 | 1.85 | 1.82 | 1.79 | 1.76 | 1.71 | 1.66 | 1.62 | 1.59 | 1.55 | 1.48 | 1.44 | 1.35 | 1.28 | 1.22 | 300 |
| 500 | 1.87 | 1.83 | 1.79 | 1.76 | 1.74 | 1.68 | 1.63 | 1.60 | 1.56 | 1.52 | 1.45 | 1.41 | 1.31 | 1.23 | 1.16 | 500 |
| 1000 | 1.85 | 1.81 | 1.77 | 1.74 | 1.72 | 1.66 | 1.61 | 1.57 | 1.54 | 1.50 | 1.43 | 1.38 | 1.28 | 1.19 | 1.11 | 1000 |
| ∞ | 1.83 | 1.79 | 1.76 | 1.72 | 1.70 | 1.64 | 1.59 | 1.55 | 1.52 | 1.47 | 1.40 | 1.36 | 1.25 | 1.15 | 1.00 | ∞ |
附表 9 q 值表
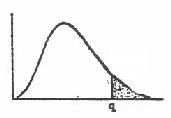
上行:P=0.05
下行:P=0.01
| n' | a(组数) | ||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 5 | 3.64 | 4.60 | 5.22 | 5.67 | 6.03 | 6.33 | 6.58 | 6.80 | 6.99 |
| 5.70 | 6.98 | 7.80 | 8.42 | 8.91 | 9.32 | 9.67 | 9.97 | 10.24 | |
| 6 | 3.46 | 4.34 | 4.90 | 5.30 | 5.63 | 5.90 | 6.12 | 6.32 | 6.49 |
| 5.24 | 6.33 | 7.03 | 7.56 | 7.97 | 8.32 | 8.61 | 8.87 | 9.10 | |
| 7 | 3.34 | 4.16 | 4.63 | 5.06 | 5.36 | 5.61 | 5.82 | 6.00 | 6.16 |
| 4.95 | 5.92 | 6.54 | 7.01 | 7.37 | 7.68 | 7.94 | 8.17 | 8.37 | |
| 8 | 3.26 | 4.04 | 4.53 | 4.89 | 5.17 | 5.40 | 5.60 | 5.77 | 5.92 |
| 4.75 | 5.64 | 6.20 | 6.62 | 6.96 | 7.24 | 7.47 | 7.68 | 7.86 | |
| 9 | 3.20 | 3.95 | 4.41 | 4.76 | 5.02 | 5.24 | 5.43 | 5.59 | 5.74 |
| 4.60 | 5.43 | 5.96 | 6.35 | 6.66 | 6.91 | 7.13 | 7.33 | 7.49 | |
| 10 | 3.15 | 3.88 | 4.33 | 4.65 | 4.91 | 5.12 | 5.30 | 5.46 | 5.60 |
| 4.48 | 5.27 | 5.77 | 6.14 | 6.43 | 6.67 | 6.87 | 7.05 | 7.21 | |
| 12 | 3.08 | 3.77 | 4.20 | 4.51 | 4.75 | 4.95 | 5.12 | 5.27 | 5.39 |
| 4.32 | 5.05 | 5.50 | 5.84 | 6.10 | 6.32 | 6.51 | 6.67 | 6.81 | |
| 14 | 3.03 | 3.70 | 4.11 | 4.41 | 4.64 | 4.83 | 4.99 | 5.13 | 5.25 |
| 4.21 | 4.89 | 5.32 | 5.63 | 5.88 | 6.08 | 6.26 | 6.41 | 6.54 | |
| 16 | 3.00 | 3.65 | 4.05 | 4.33 | 4.56 | 4.74 | 4.90 | 5.03 | 5.15 |
| 4.13 | 4.79 | 5.19 | 5.49 | 5.72 | 5.92 | 6.08 | 6.22 | 6.35 | |
| 18 | 2.97 | 3.61 | 4.00 | 4.28 | 4.49 | 4.67 | 4.82 | 4.96 | 5.07 |
| 4.07 | 4.70 | 5.09 | 5.38 | 5.60 | 5.79 | 5.94 | 6.08 | 6.20 | |
| 20 | 2.95 | 3.58 | 3.96 | 4.23 | 4.45 | 4.62 | 4.77 | 4.90 | 5.01 |
| 4.02 | 4.64 | 5.02 | 5.29 | 5.51 | 5.69 | 5.84 | 5.97 | 6.09 | |
| 30 | 2.89 | 3.49 | 3.85 | 4.10 | 4.30 | 4.46 | 4.60 | 4.72 | 4.82 |
| 3.89 | 4.45 | 4.80 | 5.05 | 5.24 | 5.40 | 5.54 | 5.65 | 5.76 | |
| 40 | 2.86 | 3.44 | 3.79 | 4.04 | 4.23 | 4.39 | 4.52 | 4.63 | 4.73 |
| 3.82 | 4.37 | 4.70 | 4.93 | 5.11 | 5.26 | 5.39 | 5.50 | 5.60 | |
| 60 | 2.83 | 3.40 | 3.74 | 3.98 | 4.16 | 4.31 | 4.44 | 4.55 | 4.65 |
| 3.76 | 4.28 | 4.59 | 4.82 | 4.99 | 5.13 | 5.25 | 5.36 | 5.45 | |
| 120 | 2.80 | 3.36 | 3.68 | 3.92 | 4.10 | 4.24 | 4.36 | 4.47 | 4.56 |
| 3.70 | 4.20 | 4.50 | 4.71 | 4.87 | 5.01 | 5.12 | 5.21 | 5.30 | |
| ∞ | 2.77 | 3.31 | 3.63 | 3.86 | 4.03 | 4.17 | 4.29 | 4.39 | 4.47 |
| 3.64 | 4.12 | 4.40 | 4.60 | 4.76 | 4.88 | 4.99 | 5.08 | 5.16 | |
附表 10 正交拉丁方表
| 3×3 | 4×4 | ||||||||
| Ⅰ | Ⅱ | Ⅰ | Ⅱ | Ⅲ | |||||
| 123 | 123 | 1234 | 1234 | 1234 | |||||
| 231 | 312 | 2143 | 3412 | 4321 | |||||
| 312 | 231 | 3412 | 4321 | 2143 | |||||
| 4321 | 2143 | 3412 | |||||||
| 5×5 | |||||||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | ||||||
| 12345 | 12345 | 12345 | 12345 | ||||||
| 23451 | 34512 | 45123 | 51234 | ||||||
| 34512 | 51234 | 23451 | 45123 | ||||||
| 45123 | 23451 | 51234 | 34512 | ||||||
| 51234 | 45123 | 34512 | 23451 | ||||||
| 7×7 | |||||||||
| Ⅰ | Ⅱ | Ⅲ | |||||||
| 1234567 | 1234567 | 1234567 | |||||||
| 2345671 | 3456712 | 4567123 | |||||||
| 3456712 | 5671234 | 7123456 | |||||||
| 4567123 | 7123456 | 3456712 | |||||||
| 5671234 | 2345671 | 6712345 | |||||||
| 6712345 | 4567123 | 2345671 | |||||||
| 7123456 | 6712345 | 5671234 | |||||||
| Ⅳ | Ⅴ | Ⅵ | |||||||
| 1234567 | 1234567 | 1234567 | |||||||
| 5671234 | 6712345 | 7123456 | |||||||
| 2345671 | 4567123 | 6712345 | |||||||
| 6712345 | 2345671 | 5671234 | |||||||
| 3456712 | 7123456 | 4567123 | |||||||
| 7123456 | 5671234 | 3456712 | |||||||
| 4567123 | 3456712 | 2345671 | |||||||
附表 11(1)相关系数界值表
| P(2): | 0.50 | 0.20 | 0.10 | 0.05 | 0.02 | 0.01 | 0.005 | 0.002 | 0.001 | |
| P(1): | 0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.0025 | 0.001 | 0.0005 | |
| 1 | 0.707 | 0.951 | 0.988 | 0.997 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| 2 | 0.500 | 0.800 | 0.900 | 0.950 | 0.980 | 0.990 | 0.995 | 0.998 | 0.999 | |
| 3 | 0.404 | 0.687 | 0.805 | 0.878 | 0.934 | 0.959 | 0.974 | 0.986 | 0.991 | |
| 4 | 0.347 | 0.603 | 0.729 | 0.811 | 0.882 | 0.917 | 0.942 | 0.963 | 0.974 | |
| 5 | 0.309 | 0.551 | 0.669 | 0.755 | 0.833 | 0.875 | 0.906 | 0.935 | 0.951 | |
| 6 | 0.281 | 0.507 | 0.621 | 0.707 | 0.789 | 0.834 | 0.870 | 0.905 | 0.925 | |
| 7 | 0.260 | 0.472 | 0.582 | 0.666 | 0.750 | 0.798 | 0.836 | 0.875 | 0.898 | |
| 8 | 0.242 | 0.443 | 0.549 | 0.632 | 0.715 | 0.765 | 0.805 | 0.847 | 0.872 | |
| 9 | 0.228 | 0.419 | 0.521 | 0.602 | 0.685 | 0.735 | 0.776 | 0.820 | 0.847 | |
| 10 | 0.216 | 0.398 | 0.497 | 0.576 | 0.658 | 0.708 | 0.750 | 0.795 | 0.823 | |
| 11 | 0.206 | 0.380 | 0.476 | 0.553 | 0.634 | 0.684 | 0.726 | 0.772 | 0.801 | |
| 12 | 0.197 | 0.365 | 0.457 | 0.532 | 0.612 | 0.661 | 0.703 | 0.750 | 0.780 | |
| 13 | 0.189 | 0.351 | 0.441 | 0.514 | 0.592 | 0.641 | 0.683 | 0.730 | 0.760 | |
| 14 | 0.182 | 0.338 | 0.426 | 0.497 | 0.574 | 0.623 | 0.664 | 0.711 | 0.742 | |
| 15 | 0.176 | 0.327 | 0.412 | 0.482 | 0.558 | 0.606 | 0.647 | 0.694 | 0.725 | |
| 16 | 0.170 | 0.317 | 0.400 | 0.468 | 0.542 | 0.590 | 0.631 | 0.678 | 0.708 | |
| 17 | 0.165 | 0.308 | 0.389 | 0.456 | 0.529 | 0.575 | 0.616 | 0.622 | 0.693 | |
| 18 | 0.160 | 0.299 | 0.378 | 0.444 | 0.515 | 0.561 | 0.602 | 0.648 | 0.679 | |
| 19 | 0.156 | 0.291 | 0.369 | 0.433 | 0.503 | 0.549 | 0.589 | 0.635 | 0.665 | |
| 20 | 0.152 | 0.284 | 0.360 | 0.423 | 0.492 | 0.537 | 0.576 | 0.622 | 0.652 | |
| 21 | 0.148 | 0.277 | 0.352 | 0.413 | 0.482 | 0.526 | 0.565 | 0.610 | 0.640 | |
| 22 | 0.145 | 0.271 | 0.344 | 0.404 | 0.472 | 0.515 | 0.554 | 0.599 | 0.629 | |
| 23 | 0.141 | 0.265 | 0.337 | 0.396 | 0.462 | 0.505 | 0.543 | 0.588 | 0.618 | |
| 24 | 0.138 | 0.260 | 0.330 | 0.388 | 0.453 | 0.496 | 0.534 | 0.578 | 0.607 | |
| 25 | 0.136 | 0.255 | 0.323 | 0.381 | 0.445 | 0.487 | 0.524 | 0.568 | 0.597 | |
| 26 | 0.133 | 0.250 | 0.317 | 0.374 | 0.437 | 0.479 | 0.515 | 0.559 | 0.588 | |
| 27 | 0.131 | 0.245 | 0.311 | 0.367 | 0.430 | 0.471 | 0.507 | 0.550 | 0.579 | |
| 28 | 0.128 | 0.241 | 0.306 | 0.361 | 0.423 | 0.463 | 0.499 | 0.541 | 0.570 | |
| 29 | 0.126 | 0.237 | 0.301 | 0.355 | 0.416 | 0.456 | 0.491 | 0.533 | 0.562 | |
| 30 | 0.124 | 0.233 | 0.296 | 0.349 | 0.409 | 0.449 | 0.484 | 0.526 | 0.554 | |
| 31 | 0.122 | 0.229 | 0.291 | 0.344 | 0.403 | 0.442 | 0.477 | 0.518 | 0.546 | |
| 32 | 0.120 | 0.226 | 0.287 | 0.339 | 0.397 | 0.436 | 0.470 | 0.511 | 0.539 | |
| 33 | 0.118 | 0.222 | 0.283 | 0.334 | 0.392 | 0.430 | 0.464 | 0.504 | 0.532 | |
| 34 | 0.116 | 0.219 | 0.279 | 0.329 | 0.386 | 0.424 | 0.458 | 0.498 | 0.525 | |
| 35 | 0.115 | 0.216 | 0.275 | 0.325 | 0.381 | 0.418 | 0.452 | 0.492 | 0.519 | |
| 36 | 0.113 | 0.213 | 0.271 | 0.320 | 0.376 | 0.413 | 0.446 | 0.486 | 0.513 | |
| 37 | 0.111 | 0.210 | 0.267 | 0.316 | 0.371 | 0.408 | 0.441 | 0.480 | 0.507 | |
| 38 | 0.110 | 0.207 | 0.264 | 0.312 | 0.367 | 0.403 | 0.435 | 0.474 | 0.501 | |
| 39 | 0.108 | 0.204 | 0.261 | 0.308 | 0.362 | 0.398 | 0.430 | 0.469 | 0.495 | |
| 40 | 0.107 | 0.202 | 0.257 | 0.304 | 0.358 | 0.393 | 0.425 | 0.463 | 0.490 | |
| 41 | 0.106 | 0.199 | 0.254 | 0.301 | 0.354 | 0.389 | 0.420 | 0.458 | 0.484 | |
| 42 | 0.104 | 0.197 | 0.251 | 0.297 | 0.350 | 0.384 | 0.416 | 0.453 | 0.479 | |
| 43 | 0.103 | 0.195 | 0.248 | 0.294 | 0.346 | 0.380 | 0.411 | 0.449 | 0.474 | |
| 44 | 0.102 | 0.192 | 0.246 | 0.291 | 0.342 | 0.376 | 0.407 | 0.444 | 0.469 | |
| 45 | 0.101 | 0.190 | 0.243 | 0.288 | 0.338 | 0.372 | 0.403 | 0.439 | 0.465 | |
| 46 | 0.100 | 0.188 | 0.240 | 0.285 | 0.335 | 0.368 | 0.399 | 0.435 | 0.460 | |
| 47 | 0.099 | 0.186 | 0.238 | 0.282 | 0.331 | 0.365 | 0.395 | 0.431 | 0.456 | |
| 48 | 0.098 | 0.184 | 0.235 | 0.270 | 0.328 | 0.361 | 0.391 | 0.427 | 0.451 | |
| 49 | 0.097 | 0.182 | 0.233 | 0.276 | 0.325 | 0.358 | 0.387 | 0.423 | 0.447 | |
| 50 | 0.096 | 0.181 | 0.231 | 0.273 | 0.322 | 0.354 | 0.384 | 0.419 | 0.443 |
附表 11 (2)相关系数界值表
| P(2): | 0.50 | 0.20 | 0.10 | 0.05 | 0.02 | 0.01 | 0.005 | 0.002 | 0.001 | |
| P(1): | 0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.0025 | 0.001 | 0.0005 | |
| 52 | 0.094 | 0.177 | 0.226 | 0.268 | 0.316 | 0.348 | 0.377 | 0.411 | 0.435 | |
| 54 | 0.092 | 0.174 | 0.222 | 0.263 | 0.310 | 0.341 | 0.370 | 0.404 | 0.428 | |
| 56 | 0.090 | 0.171 | 0.218 | 0.259 | 0.305 | 0.336 | 0.364 | 0.398 | 0.421 | |
| 58 | 0.089 | 0.168 | 0.214 | 0.254 | 0.300 | 0.330 | 0.358 | 0.391 | 0.414 | |
| 60 | 0.087 | 0.165 | 0.211 | 0.250 | 0.295 | 0.325 | 0.352 | 0.385 | 0.408 | |
| 62 | 0.086 | 0.162 | 0.207 | 0.246 | 0.290 | 0.320 | 0.347 | 0.379 | 0.402 | |
| 64 | 0.081 | 0.160 | 0.204 | 0.242 | 0.286 | 0.315 | 0.342 | 0.374 | 0.396 | |
| 66 | 0.083 | 0.157 | 0.201 | 0.239 | 0.282 | 0.310 | 0.337 | 0.368 | 0.390 | |
| 68 | 0.082 | 0.155 | 0.198 | 0.235 | 0.278 | 0.306 | 0.332 | 0.363 | 0.385 | |
| 70 | 0.081 | 0.153 | 0.195 | 0.232 | 0.274 | 0.302 | 0.327 | 0.358 | 0.380 | |
| 72 | 0.080 | 0.151 | 0.193 | 0.229 | 0.270 | 0.298 | 0.323 | 0.354 | 0.375 | |
| 74 | 0.079 | 0.149 | 0.190 | 0.226 | 0.266 | 0.294 | 0.319 | 0.349 | 0.370 | |
| 76 | 0.078 | 0.147 | 0.188 | 0.223 | 0.263 | 0.290 | 0.315 | 0.345 | 0.365 | |
| 78 | 0.077 | 0.145 | 0.185 | 0.220 | 0.260 | 0.286 | 0.311 | 0.340 | 0.361 | |
| 80 | 0.076 | 0.143 | 0.183 | 0.217 | 0.257 | 0.283 | 0.307 | 0.336 | 0.357 | |
| 82 | 0.075 | 0.141 | 0.181 | 0.215 | 0.253 | 0.280 | 0.304 | 0.333 | 0.328 | |
| 84 | 0.074 | 0.140 | 0.179 | 0.212 | 0.251 | 0.276 | 0.300 | 0.329 | 0.349 | |
| 86 | 0.073 | 0.138 | 0.177 | 0.210 | 0.248 | 0.273 | 0.297 | 0.325 | 0.345 | |
| 88 | 0.072 | 0.136 | 0.174 | 0.207 | 0.245 | 0.270 | 0.293 | 0.321 | 0.341 | |
| 90 | 0.071 | 0.135 | 0.173 | 0.205 | 0.242 | 0.267 | 0.290 | 0.318 | 0.338 | |
| 92 | 0.070 | 0.133 | 0.171 | 0.203 | 0.240 | 0.264 | 0.287 | 0.315 | 0.334 | |
| 94 | 0.070 | 0.132 | 0.169 | 0.201 | 0.237 | 0.262 | 0.284 | 0.312 | 0.331 | |
| 96 | 0.069 | 0.131 | 0.167 | 0.199 | 0.235 | 0.259 | 0.281 | 0.308 | 0.327 | |
| 98 | 0.068 | 0.129 | 0.165 | 0.197 | 0.232 | 0.256 | 0.279 | 0.305 | 0.324 | |
| 100 | 0.068 | 0.128 | 0.164 | 0.195 | 0.230 | 0.254 | 0.276 | 0.303 | 0.321 | |
| 105 | 0.066 | 0.125 | 0.160 | 0.190 | 0.225 | 0.248 | 0.270 | 0.296 | 0.314 | |
| 110 | 0.064 | 0.122 | 0.156 | 0.186 | 0.220 | 0.242 | 0.264 | 0.289 | 0.307 | |
| 115 | 0.063 | 0.119 | 0.153 | 0.182 | 0.215 | 0.237 | 0.258 | 0.283 | 0.300 | |
| 120 | 0.062 | 0.117 | 0.150 | 0.178 | 0.210 | 0.232 | 0.253 | 0.277 | 0.294 | |
| 125 | 0.060 | 0.114 | 0.147 | 0.174 | 0.206 | 0.228 | 0.248 | 0.272 | 0.289 | |
| 130 | 0.059 | 0.112 | 0.144 | 0.171 | 0.202 | 0.223 | 0.243 | 0.267 | 0.283 | |
| 135 | 0.058 | 0.110 | 0.141 | 0.168 | 0.199 | 0.219 | 0.239 | 0.262 | 0.278 | |
| 140 | 0.057 | 0.108 | 0.139 | 0.165 | 0.195 | 0.215 | 0.234 | 0.257 | 0.273 | |
| 145 | 0.056 | 0.106 | 0.136 | 0.162 | 0.192 | 0.212 | 0.230 | 0.253 | 0.269 | |
| 150 | 0.055 | 0.105 | 0.134 | 0.159 | 0.189 | 0.208 | 0.227 | 0.249 | 0.264 | |
| 160 | 0.053 | 0.101 | 0.130 | 0.154 | 0.183 | 0.202 | 0.220 | 0.241 | 0.256 | |
| 170 | 0.052 | 0.098 | 0.126 | 0.150 | 0.177 | 0.196 | 0.213 | 0.234 | 0.249 | |
| 180 | 0.050 | 0.095 | 0.122 | 0.145 | 0.172 | 0.190 | 0.207 | 0.228 | 0.242 | |
| 190 | 0.049 | 0.093 | 0.119 | 0.142 | 0.168 | 0.185 | 0.202 | 0.222 | 0.236 | |
| 200 | 0.048 | 0.091 | 0.116 | 0.138 | 0.164 | 0.181 | 0.197 | 0.216 | 0.230 | |
| 250 | 0.043 | 0.081 | 0.104 | 0.124 | 0.146 | 0.162 | 0.176 | 0.194 | 0.206 | |
| 300 | 0.039 | 0.074 | 0.095 | 0.113 | 0.134 | 0.148 | 0.161 | 0.177 | 0.188 | |
| 350 | 0.036 | 0.068 | 0.088 | 0.105 | 0.124 | 0.137 | 0.149 | 0.164 | 0.175 | |
| 400 | 0.034 | 0.064 | 0.082 | 0.098 | 0.116 | 0.128 | 0.140 | 0.154 | 0.164 | |
| 450 | 0.032 | 0.060 | 0.077 | 0.092 | 0.109 | 0.121 | 0.132 | 0.145 | 0.154 | |
| 500 | 0.030 | 0.057 | 0.074 | 0.088 | 0.104 | 0.115 | 0.125 | 0.138 | 0.146 | |
| 600 | 0.028 | 0.052 | 0.067 | 0.080 | 0.095 | 0.105 | 0.114 | 0.126 | 0.134 | |
| 700 | 0.026 | 0.048 | 0.062 | 0.074 | 0.088 | 0.097 | 0.106 | 0.116 | 0.124 | |
| 800 | 0.024 | 0.045 | 0.058 | 0.060 | 0.082 | 0.091 | 0.099 | 0.109 | 0.116 | |
| 900 | 0.022 | 0.043 | 0.055 | 0.065 | 0.077 | 0.086 | 0.093 | 0.103 | 0.100 | |
| 1000 | 0.021 | 0.041 | 0.052 | 0.062 | 0.073 | 0.081 | 0.089 | 0.098 | 0.104 |
附表 12 成对资料秩和检验 R 的界值表
| 对子数 (n) | 较小的秩号之和 | 对子数 ((n) | 较小的秩号之和 | ||
| P=0.05 | P=0.01 | P=0.05 | P=0.01 | ||
| 6 | — | 16 | 30 | 20 | |
| 7 | 2 | — | 17 | 35 | 23 |
| 8 | 4 | 18 | 40 | 28 | |
| 9 | 6 | 2 | 19 | 46 | 32 |
| 10 | 8 | 3 | 20 | 52 | 38 |
| 11 | 11 | 5 | 21 | 59 | 43 |
| 12 | 14 | 7 | 22 | 66 | 49 |
| 13 | 17 | 10 | 23 | 73 | 55 |
| 14 | 21 | 13 | 24 | 81 | 61 |
| 15 | 25 | 16 | 25 | 89 | 68 |
附表 13 两组资料秩和检验较小 R 值的界值表(双侧检验)
| n2= 较大 n | P | n1= 较小 n | |||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
| 4 | 0.05 | 10 | |||||||||||||
| 0.01 | — | ||||||||||||||
| 5 | 0.05 | 6 | 11 | 17 | |||||||||||
| 0.01 | — | — | 15 | ||||||||||||
| 6 | 0.05 | 7 | 12 | 18 | 26 | ||||||||||
| 0.01 | — | 10 | 16 | 23 | |||||||||||
| 7 | 0.05 | 7 | 13 | 20 | 27 | 36 | |||||||||
| 0.01 | — | 10 | 17 | 24 | 32 | ||||||||||
| 8 | 0.05 | 3 | 8 | 14 | 21 | 29 | 38 | 49 | |||||||
| 0.01 | — | — | 11 | 17 | 25 | 34 | 43 | ||||||||
| 9 | 0.05 | 3 | 8 | 15 | 22 | 31 | 40 | 51 | 63 | ||||||
| 0.01 | — | 6 | 11 | 18 | 26 | 35 | 45 | 56 | |||||||
| 10 | 0.05 | 3 | 9 | 15 | 23 | 32 | 42 | 53 | 65 | 78 | |||||
| 0.01 | — | 6 | 12 | 19 | 27 | 37 | 47 | 58 | 71 | ||||||
| 11 | 0.05 | 4 | 9 | 16 | 24 | 34 | 44 | 55 | 68 | 81 | 96 | ||||
| 0.01 | — | 6 | 12 | 20 | 28 | 38 | 49 | 61 | 74 | 87 | |||||
| 12 | 0.05 | 4 | 10 | 17 | 26 | 35 | 46 | 58 | 71 | 85 | 99 | 115 | |||
| 0.01 | — | 7 | 13 | 21 | 30 | 40 | 51 | 63 | 76 | 90 | 106 | ||||
| 13 | 0.05 | 4 | 10 | 18 | 27 | 37 | 48 | 60 | 73 | 88 | 103 | 119 | 137 | ||
| 0.01 | — | 7 | 14 | 22 | 31 | 41 | 53 | 65 | 79 | 93 | 109 | 125 | |||
| 14 | 0.05 | 4 | 11 | 19 | 28 | 38 | 50 | 63 | 76 | 91 | 106 | 123 | 141 | 160 | |
| 0.01 | — | 7 | 14 | 22 | 32 | 43 | 54 | 67 | 81 | 96 | 112 | 129 | 147 | ||
| 15 | 0.05 | 4 | 11 | 20 | 29 | 40 | 52 | 65 | 79 | 94 | 110 | 127 | 145 | 164 | 185 |
| 0.01 | — | 8 | 15 | 23 | 33 | 44 | 56 | 70 | 84 | 99 | 115 | 133 | 151 | 171 | |
| 16 | 0.05 | 4 | 12 | 21 | 31 | 42 | 54 | 67 | 82 | 97 | 114 | 131 | 150 | 169 | |
| 0.01 | — | 8 | 15 | 24 | 34 | 46 | 58 | 72 | 86 | 102 | 119 | 137 | 155 | ||
| 17 | 0.05 | 5 | 12 | 21 | 32 | 43 | 56 | 70 | 84 | 100 | 117 | 135 | 154 | ||
| 0.01 | — | 8 | 16 | 25 | 36 | 47 | 60 | 74 | 89 | 105 | 122 | 140 | |||
| 18 | 0.05 | 5 | 13 | 22 | 33 | 45 | 58 | 72 | 87 | 103 | 121 | 139 | |||
| 0.01 | — | 8 | 16 | 26 | 37 | 49 | 62 | 76 | 92 | 108 | 125 | ||||
| 19 | 0.05 | 5 | 13 | 23 | 34 | 46 | 60 | 74 | 90 | 107 | 124 | ||||
| 0.01 | 3 | 9 | 17 | 27 | 38 | 50 | 64 | 78 | 94 | 111 | |||||
| 20 | 0.05 | 5 | 14 | 24 | 35 | 48 | 62 | 77 | 93 | 110 | |||||
| 0.01 | 3 | 9 | 18 | 28 | 39 | 52 | 66 | 81 | 97 | ||||||
| 21 | 0.05 | 6 | 14 | 25 | 37 | 50 | 64 | 79 | 95 | ||||||
| 0.01 | 3 | 9 | 18 | 29 | 40 | 53 | 68 | 83 | |||||||
| 22 | 0.05 | 6 | 15 | 26 | 38 | 51 | 66 | 82 | |||||||
| 0.01 | 3 | 10 | 19 | 29 | 42 | 55 | 70 | ||||||||
| 23 | 0.05 | 6 | 15 | 27 | 39 | 53 | 68 | ||||||||
| 0.01 | 3 | 10 | 19 | 30 | 43 | 57 | |||||||||
| 24 | 0.05 | 6 | 16 | 28 | 40 | 55 | |||||||||
| 0.01 | 3 | 10 | 20 | 31 | 44 | ||||||||||
| 25 | 0.05 | 6 | 16 | 28 | 42 | ||||||||||
| 0.01 | 3 | 11 | 20 | 32 | |||||||||||
| 26 | 0.05 | 7 | 17 | 29 | |||||||||||
| 0.01 | 3 | 11 | 21 | ||||||||||||
| 27 | 0.05 | 7 | 17 | ||||||||||||
| 0.01 | 4 | 11 | |||||||||||||
| 28 | 0.05 | 7 | |||||||||||||
| 0.01 | 4 | ||||||||||||||
附表 14 三组完全随机设计秩和检验的界值表
| N | n1 | n2 | n3 | H0.05 | H0.01 | N | n1 | n2 | n3 | H0.05 | H0.01 |
| 7 | 3 | 2 | 2 | 4.71 | 5 | 3 | 2 | 5.25 | 6.82 | ||
| 3 | 3 | 1 | 5.14 | 5 | 4 | 1 | 4.99 | 6.95 | |||
| 8 | 3 | 3 | 2 | 5.36 | 11 | 4 | 4 | 3 | 5.60 | 7.14 | |
| 4 | 2 | 2 | 5.33 | 5 | 3 | 3 | 5.65 | 7.08 | |||
| 4 | 3 | 1 | 5.20 | 5 | 4 | 2 | 5.27 | 7.12 | |||
| 5 | 2 | 1 | 5.00 | 5 | 5 | 1 | 5.13 | 7.31 | |||
| 9 | 3 | 3 | 3 | 5.60 | 7.20 | 12 | 4 | 4 | 4 | 5.69 | 7.65 |
| 4 | 3 | 2 | 5.44 | 6.30 | 5 | 4 | 3 | 5.63 | 7.44 | ||
| 4 | 4 | 1 | 4.97 | 6.67 | 5 | 5 | 2 | 5.34 | 7.27 | ||
| 5 | 2 | 2 | 5.16 | 6.53 | 13 | 5 | 4 | 4 | 5.62 | 7.76 | |
| 5 | 3 | 1 | 4.96 | 6.40 | 5 | 5 | 3 | 5.71 | 7.54 | ||
| 10 | 4 | 3 | 3 | 5.72 | 6.75 | 14 | 5 | 5 | 4 | 5.64 | 7.79 |
| 4 | 4 | 2 | 5.45 | 7.04 | 15 | 5 | 5 | 5 | 5.78 | 7.98 |
附表 15 附机单位组设计秩和检验的界值表
| 单位组数 | 三个处理组 | 四个处理组 | ||
| H0.05 | H0.01 | H0.05 | H0.01 | |
| 2 | – | – | 6.00 | – |
| 3 | 6.00 | – | 7.40 | 9.00 |
| 4 | 6.50 | 8.00 | 7.80 | 9.60 |
| 5 | 6.40 | 8.40 | 7.80 | 9.96 |
| 6 | 7.00 | 9.00 | 7.60 | 10.20 |
| 7 | 7.14 | 8.86 | 7.80 | 10.37 |
| 8 | 6.25 | 9.00 | ||
| 9 | 6.22 | 8.67 | ||
| 10 | 6.20 | 9.60 | ||
| 11 | 6.55 | 9.46 | ||
| 12 | 6.17 | 9.50 | ||
| 13 | 6.00 | 9.39 | ||
| 14 | 6.14 | 9.00 | ||
| 15 | 6.40 | 8.93 | ||
附表 16 Spearman 秩相关系数界值表
| n | rs0.05 | rs0.01 | n | rs0.05 | rs0.01 |
| 6 | 0.886 | 1.000 | 31 | 0.356 | 0.459 |
| 7 | 0.786 | 0.929 | 32 | 0.350 | 0.452 |
| 8 | 0.738 | 0.881 | 33 | 0.345 | 0.446 |
| 9 | 0.700 | 0.833 | 34 | 0.340 | 0.439 |
| 10 | 0.648 | 0.794 | 35 | 0.335 | 0.433 |
| 11 | 0.618 | 0.755 | 36 | 0.330 | 0.427 |
| 12 | 0.587 | 0.727 | 37 | 0.325 | 0.421 |
| 13 | 0.560 | 0.703 | 38 | 0.321 | 0.415 |
| 14 | 0.538 | 0.679 | 39 | 0.317 | 0.410 |
| 15 | 0.521 | 0.654 | 40 | 0.313 | 0.405 |
| 16 | 0.503 | 0.635 | 41 | 0.309 | 0.400 |
| 17 | 0.485 | 0.615 | 42 | 0.305 | 0.395 |
| 18 | 0.472 | 0.600 | 43 | 0.301 | 0.391 |
| 19 | 0.460 | 0.584 | 44 | 0.298 | 0.386 |
| 20 | 0.447 | 0.570 | 45 | 0.294 | 0.382 |
| 21 | 0.435 | 0.556 | 46 | 0.291 | 0.378 |
| 22 | 0.425 | 0.544 | 47 | 0.288 | 0.374 |
| 23 | 0.415 | 0.532 | 48 | 0.285 | 0.370 |
| 24 | 0.406 | 0.521 | 49 | 0.282 | 0.366 |
| 25 | 0.398 | 0.511 | 50 | 0.297 | 0.363 |
| 26 | 0.390 | 0.501 | |||
| 27 | 0.382 | 0.491 | |||
| 28 | 0.375 | 0.483 | |||
| 29 | 0.368 | 0.475 | |||
| 30 | 0.362 | 0.467 |
附表 17(1)随机数字表
| 编号 | 1 | 2 | 3 | 5 | 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 1 | 03 | 47 | 43 | 73 | 86 | 36 | 96 | 47 | 36 | 61 | 46 | 98 | 63 | 71 | 62 | 33 | 26 | 16 | 80 | 45 | 60 | 11 | 14 | 10 | 95 |
| 2 | 97 | 74 | 24 | 67 | 62 | 42 | 81 | 14 | 57 | 20 | 42 | 53 | 32 | 37 | 32 | 27 | 07 | 36 | 07 | 51 | 24 | 51 | 79 | 89 | 73 |
| 3 | 16 | 76 | 62 | 27 | 66 | 56 | 50 | 26 | 71 | 07 | 32 | 90 | 79 | 78 | 53 | 13 | 55 | 38 | 58 | 59 | 88 | 97 | 54 | 14 | 10 |
| 4 | 12 | 56 | 85 | 99 | 26 | 96 | 96 | 68 | 27 | 31 | 05 | 03 | 72 | 93 | 15 | 57 | 12 | 10 | 14 | 21 | 88 | 26 | 49 | 81 | 76 |
| 5 | 55 | 59 | 56 | 35 | 64 | 38 | 54 | 82 | 46 | 22 | 31 | 62 | 43 | 09 | 90 | 06 | 18 | 44 | 32 | 53 | 23 | 83 | 01 | 30 | 30 |
| 6 | 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 | 84 | 26 | 34 | 91 | 64 |
| 7 | 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 | 83 | 92 | 12 | 06 | 76 |
| 8 | 63 | 01 | 63 | 78 | 59 | 16 | 95 | 55 | 67 | 19 | 98 | 10 | 50 | 71 | 75 | 12 | 86 | 73 | 58 | 07 | 44 | 39 | 52 | 38 | 79 |
| 9 | 33 | 21 | 12 | 34 | 29 | 78 | 64 | 56 | 07 | 82 | 52 | 42 | 07 | 44 | 38 | 15 | 51 | 00 | 13 | 42 | 99 | 66 | 02 | 79 | 54 |
| 10 | 57 | 60 | 86 | 32 | 44 | 09 | 47 | 27 | 96 | 54 | 49 | 17 | 46 | 09 | 62 | 90 | 52 | 84 | 77 | 27 | 08 | 02 | 73 | 43 | 28 |
| 11 | 18 | 18 | 07 | 92 | 46 | 44 | 17 | 16 | 58 | 09 | 79 | 83 | 86 | 19 | 62 | 06 | 76 | 50 | 03 | 10 | 55 | 23 | 64 | 05 | 05 |
| 12 | 26 | 62 | 38 | 97 | 75 | 84 | 16 | 07 | 44 | 99 | 83 | 11 | 46 | 32 | 24 | 20 | 14 | 85 | 88 | 45 | 10 | 93 | 72 | 88 | 71 |
| 13 | 23 | 42 | 40 | 64 | 74 | 82 | 97 | 77 | 77 | 81 | 07 | 45 | 32 | 14 | 08 | 32 | 98 | 94 | 07 | 72 | 93 | 85 | 79 | 10 | 75 |
| 14 | 52 | 36 | 28 | 19 | 95 | 50 | 92 | 26 | 11 | 97 | 00 | 56 | 76 | 31 | 38 | 80 | 22 | 02 | 53 | 53 | 86 | 60 | 42 | 04 | 53 |
| 15 | 37 | 85 | 94 | 35 | 12 | 83 | 39 | 50 | 08 | 30 | 42 | 34 | 07 | 96 | 88 | 54 | 42 | 06 | 87 | 98 | 35 | 85 | 29 | 48 | 39 |
| 16 | 70 | 29 | 17 | 12 | 13 | 40 | 33 | 20 | 38 | 26 | 13 | 89 | 51 | 03 | 74 | 17 | 76 | 37 | 13 | 04 | 07 | 74 | 21 | 19 | 30 |
| 17 | 56 | 62 | 18 | 37 | 35 | 96 | 83 | 50 | 87 | 75 | 97 | 12 | 25 | 93 | 47 | 70 | 33 | 24 | 03 | 54 | 97 | 77 | 46 | 44 | 80 |
| 18 | 99 | 49 | 57 | 22 | 77 | 88 | 42 | 95 | 45 | 72 | 16 | 64 | 36 | 16 | 00 | 04 | 43 | 18 | 66 | 79 | 94 | 77 | 24 | 21 | 90 |
| 19 | 16 | 08 | 15 | 04 | 72 | 33 | 27 | 14 | 34 | 09 | 45 | 59 | 34 | 68 | 49 | 12 | 72 | 07 | 34 | 45 | 99 | 27 | 72 | 95 | 14 |
| 20 | 31 | 16 | 93 | 32 | 43 | 50 | 27 | 89 | 87 | 19 | 20 | 15 | 37 | 00 | 49 | 52 | 85 | 66 | 60 | 44 | 38 | 68 | 88 | 11 | 80 |
| 21 | 68 | 34 | 30 | 13 | 70 | 55 | 74 | 30 | 77 | 40 | 44 | 22 | 78 | 84 | 26 | 04 | 33 | 46 | 09 | 52 | 68 | 07 | 97 | 06 | 57 |
| 22 | 74 | 57 | 25 | 65 | 76 | 59 | 29 | 97 | 68 | 60 | 71 | 91 | 38 | 67 | 54 | 13 | 58 | 18 | 24 | 76 | 15 | 54 | 55 | 95 | 52 |
| 23 | 27 | 42 | 37 | 86 | 53 | 48 | 55 | 90 | 65 | 72 | 96 | 57 | 69 | 36 | 10 | 96 | 46 | 92 | 42 | 45 | 97 | 60 | 49 | 04 | 91 |
| 24 | 00 | 39 | 68 | 29 | 61 | 66 | 37 | 32 | 20 | 30 | 77 | 84 | 57 | 03 | 29 | 10 | 45 | 65 | 04 | 26 | 11 | 04 | 96 | 67 | 24 |
| 25 | 29 | 94 | 98 | 94 | 24 | 68 | 49 | 69 | 10 | 82 | 53 | 75 | 91 | 93 | 30 | 34 | 25 | 20 | 57 | 27 | 40 | 48 | 73 | 51 | 92 |
| 26 | 16 | 90 | 82 | 66 | 59 | 83 | 62 | 64 | 11 | 12 | 67 | 19 | 00 | 71 | 74 | 60 | 47 | 21 | 29 | 68 | 02 | 02 | 37 | 03 | 31 |
| 27 | 11 | 27 | 94 | 75 | 06 | 06 | 09 | 19 | 74 | 66 | 02 | 94 | 37 | 34 | 02 | 76 | 70 | 90 | 30 | 86 | 38 | 45 | 94 | 30 | 38 |
| 28 | 35 | 24 | 10 | 16 | 20 | 33 | 32 | 51 | 26 | 38 | 79 | 78 | 45 | 04 | 91 | 16 | 92 | 53 | 56 | 16 | 02 | 75 | 50 | 95 | 98 |
| 29 | 38 | 23 | 16 | 86 | 38 | 42 | 38 | 97 | 01 | 50 | 87 | 75 | 66 | 81 | 41 | 40 | 01 | 74 | 91 | 62 | 48 | 51 | 84 | 08 | 32 |
| 30 | 31 | 96 | 25 | 91 | 47 | 96 | 44 | 33 | 49 | 13 | 34 | 86 | 82 | 53 | 91 | 00 | 52 | 43 | 48 | 85 | 27 | 55 | 26 | 89 | 62 |
| 31 | 66 | 67 | 40 | 67 | 14 | 64 | 05 | 71 | 95 | 86 | 11 | 05 | 65 | 09 | 68 | 76 | 83 | 20 | 37 | 90 | 57 | 16 | 00 | 11 | 66 |
| 32 | 14 | 90 | 84 | 45 | 11 | 75 | 73 | 88 | 05 | 90 | 52 | 27 | 41 | 14 | 86 | 22 | 98 | 12 | 22 | 08 | 07 | 52 | 74 | 95 | 80 |
| 33 | 68 | 05 | 51 | 18 | 00 | 33 | 96 | 02 | 75 | 19 | 07 | 60 | 62 | 93 | 55 | 59 | 33 | 82 | 43 | 90 | 49 | 37 | 38 | 44 | 59 |
| 34 | 20 | 46 | 78 | 73 | 90 | 97 | 51 | 40 | 14 | 02 | 04 | 02 | 33 | 31 | 08 | 39 | 54 | 16 | 49 | 36 | 47 | 95 | 93 | 13 | 30 |
| 35 | 64 | 19 | 58 | 97 | 79 | 15 | 06 | 15 | 93 | 20 | 01 | 90 | 10 | 75 | 06 | 40 | 78 | 73 | 89 | 62 | 02 | 67 | 74 | 17 | 33 |
| 36 | 05 | 26 | 93 | 70 | 60 | 22 | 35 | 85 | 15 | 13 | 92 | 03 | 51 | 59 | 77 | 59 | 56 | 78 | 06 | 83 | 52 | 91 | 05 | 70 | 74 |
| 37 | 07 | 97 | 10 | 88 | 23 | 09 | 98 | 42 | 99 | 64 | 61 | 71 | 62 | 99 | 15 | 06 | 51 | 29 | 16 | 93 | 58 | 05 | 77 | 09 | 51 |
| 38 | 68 | 71 | 86 | 85 | 85 | 54 | 87 | 66 | 47 | 54 | 73 | 32 | 08 | 11 | 12 | 44 | 95 | 92 | 63 | 16 | 29 | 56 | 24 | 29 | 48 |
| 39 | 26 | 99 | 61 | 65 | 53 | 58 | 37 | 78 | 80 | 70 | 42 | 10 | 50 | 67 | 42 | 32 | 17 | 55 | 85 | 74 | 94 | 44 | 67 | 16 | 94 |
| 40 | 14 | 65 | 52 | 68 | 75 | 87 | 59 | 36 | 22 | 41 | 26 | 78 | 63 | 06 | 55 | 13 | 08 | 27 | 01 | 50 | 15 | 29 | 39 | 39 | 43 |
| 41 | 17 | 53 | 77 | 58 | 71 | 71 | 41 | 61 | 50 | 72 | 12 | 41 | 94 | 96 | 26 | 44 | 95 | 27 | 36 | 99 | 02 | 96 | 74 | 30 | 83 |
| 42 | 90 | 26 | 59 | 21 | 19 | 23 | 52 | 23 | 33 | 12 | 96 | 93 | 02 | 18 | 39 | 07 | 02 | 18 | 36 | 07 | 25 | 99 | 32 | 70 | 23 |
| 43 | 41 | 23 | 52 | 55 | 99 | 31 | 04 | 49 | 69 | 96 | 10 | 47 | 48 | 45 | 88 | 13 | 41 | 43 | 89 | 20 | 97 | 17 | 14 | 49 | 17 |
| 44 | 60 | 20 | 50 | 81 | 69 | 31 | 99 | 73 | 68 | 68 | 35 | 81 | 33 | 03 | 76 | 24 | 30 | 12 | 48 | 60 | 18 | 99 | 10 | 72 | 34 |
| 45 | 91 | 25 | 38 | 05 | 90 | 94 | 58 | 28 | 41 | 36 | 45 | 37 | 59 | 03 | 09 | 90 | 35 | 57 | 29 | 12 | 82 | 62 | 54 | 65 | 60 |
| 46 | 34 | 50 | 57 | 74 | 37 | 98 | 80 | 33 | 00 | 91 | 09 | 77 | 93 | 19 | 82 | 74 | 94 | 80 | 04 | 04 | 45 | 07 | 31 | 66 | 49 |
| 47 | 85 | 22 | 04 | 39 | 43 | 73 | 81 | 53 | 94 | 79 | 33 | 62 | 46 | 86 | 28 | 08 | 31 | 54 | 46 | 31 | 53 | 94 | 13 | 38 | 47 |
| 48 | 09 | 79 | 13 | 77 | 48 | 73 | 82 | 97 | 22 | 21 | 05 | 03 | 27 | 24 | 83 | 72 | 89 | 44 | 05 | 60 | 35 | 80 | 39 | 94 | 88 |
| 49 | 88 | 75 | 80 | 18 | 14 | 22 | 95 | 75 | 42 | 49 | 39 | 32 | 82 | 22 | 49 | 02 | 48 | 07 | 70 | 37 | 16 | 04 | 61 | 67 | 87 |
| 50 | 90 | 96 | 23 | 70 | 00 | 39 | 00 | 03 | 06 | 90 | 55 | 85 | 78 | 38 | 36 | 94 | 37 | 30 | 69 | 32 | 90 | 89 | 00 | 76 | 33 |
附表 17(2)随机数字表
| 编号 | 1 | 2 | 3 | 5 | 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 1 | 53 | 74 | 23 | 99 | 67 | 61 | 32 | 28 | 69 | 84 | 94 | 62 | 67 | 86 | 24 | 98 | 33 | 41 | 19 | 95 | 47 | 53 | 53 | 38 | 09 |
| 2 | 63 | 38 | 06 | 86 | 54 | 99 | 00 | 65 | 26 | 94 | 02 | 82 | 90 | 23 | 07 | 79 | 62 | 67 | 80 | 60 | 75 | 91 | 12 | 81 | 19 |
| 3 | 35 | 30 | 58 | 21 | 46 | 06 | 72 | 17 | 10 | 94 | 25 | 21 | 31 | 75 | 96 | 49 | 28 | 24 | 00 | 49 | 55 | 65 | 79 | 78 | 07 |
| 4 | 63 | 43 | 36 | 82 | 69 | 65 | 51 | 18 | 37 | 88 | 61 | 38 | 44 | 12 | 45 | 32 | 92 | 85 | 88 | 65 | 54 | 34 | 81 | 85 | 35 |
| 5 | 98 | 25 | 37 | 55 | 26 | 01 | 91 | 82 | 81 | 46 | 74 | 71 | 12 | 94 | 97 | 24 | 02 | 71 | 37 | 07 | 03 | 92 | 18 | 66 | 75 |
| 6 | 02 | 63 | 21 | 17 | 69 | 71 | 50 | 80 | 89 | 56 | 38 | 15 | 70 | 11 | 48 | 43 | 40 | 45 | 86 | 98 | 00 | 83 | 26 | 91 | 03 |
| 7 | 64 | 55 | 22 | 21 | 82 | 48 | 22 | 28 | 06 | 00 | 61 | 54 | 13 | 43 | 91 | 82 | 78 | 12 | 23 | 29 | 06 | 66 | 24 | 12 | 27 |
| 8 | 85 | 07 | 26 | 13 | 89 | 01 | 10 | 07 | 82 | 04 | 59 | 63 | 69 | 36 | 03 | 69 | 11 | 15 | 83 | 80 | 13 | 29 | 54 | 19 | 28 |
| 9 | 58 | 54 | 16 | 24 | 15 | 51 | 54 | 44 | 82 | 00 | 62 | 61 | 65 | 04 | 69 | 38 | 18 | 65 | 18 | 97 | 85 | 72 | 13 | 49 | 21 |
| 10 | 34 | 85 | 27 | 84 | 87 | 61 | 48 | 64 | 56 | 26 | 90 | 18 | 48 | 13 | 26 | 37 | 70 | 15 | 42 | 57 | 65 | 65 | 80 | 39 | 07 |
| 11 | 03 | 92 | 18 | 27 | 46 | 57 | 99 | 16 | 96 | 56 | 30 | 33 | 72 | 85 | 22 | 84 | 64 | 38 | 56 | 98 | 99 | 01 | 30 | 98 | 64 |
| 12 | 62 | 95 | 30 | 27 | 59 | 37 | 75 | 41 | 66 | 48 | 86 | 97 | 80 | 61 | 45 | 23 | 53 | 04 | 01 | 63 | 45 | 76 | 08 | 64 | 27 |
| 13 | 08 | 45 | 93 | 15 | 22 | 60 | 21 | 75 | 46 | 91 | 98 | 77 | 27 | 85 | 42 | 28 | 88 | 61 | 08 | 84 | 69 | 62 | 03 | 42 | 73 |
| 14 | 07 | 08 | 55 | 18 | 40 | 45 | 44 | 75 | 13 | 90 | 24 | 94 | 96 | 61 | 02 | 57 | 55 | 66 | 83 | 15 | 73 | 42 | 37 | 11 | 61 |
| 15 | 01 | 85 | 89 | 95 | 66 | 51 | 10 | 19 | 34 | 88 | 15 | 84 | 97 | 19 | 75 | 12 | 76 | 39 | 43 | 78 | 64 | 63 | 91 | 08 | 25 |
| 16 | 72 | 84 | 71 | 14 | 35 | 19 | 11 | 58 | 49 | 26 | 50 | 11 | 17 | 17 | 76 | 86 | 31 | 57 | 20 | 18 | 95 | 60 | 78 | 46 | 75 |
| 17 | 88 | 78 | 28 | 16 | 84 | 13 | 52 | 53 | 94 | 53 | 75 | 45 | 69 | 30 | 96 | 73 | 89 | 65 | 70 | 31 | 99 | 17 | 43 | 48 | 76 |
| 18 | 45 | 17 | 75 | 65 | 57 | 28 | 40 | 19 | 72 | 12 | 25 | 12 | 74 | 75 | 67 | 60 | 40 | 60 | 81 | 19 | 24 | 62 | 01 | 61 | 16 |
| 19 | 96 | 76 | 28 | 12 | 54 | 22 | 01 | 11 | 94 | 25 | 71 | 96 | 16 | 16 | 88 | 68 | 64 | 36 | 74 | 45 | 19 | 59 | 60 | 88 | 92 |
| 20 | 43 | 31 | 67 | 72 | 30 | 24 | 02 | 94 | 08 | 63 | 38 | 32 | 36 | 66 | 02 | 69 | 36 | 38 | 25 | 39 | 48 | 03 | 45 | 15 | 22 |
| 21 | 50 | 44 | 66 | 44 | 21 | 66 | 06 | 58 | 05 | 62 | 63 | 15 | 54 | 35 | 02 | 42 | 35 | 48 | 96 | 32 | 14 | 52 | 41 | 52 | 48 |
| 22 | 22 | 66 | 22 | 15 | 86 | 26 | 63 | 75 | 41 | 99 | 58 | 42 | 36 | 72 | 24 | 58 | 37 | 52 | 18 | 51 | 03 | 37 | 18 | 39 | 11 |
| 23 | 96 | 24 | 40 | 14 | 51 | 23 | 22 | 30 | 88 | 57 | 95 | 67 | 47 | 29 | 83 | 94 | 69 | 40 | 06 | 07 | 18 | 16 | 36 | 78 | 86 |
| 24 | 31 | 73 | 91 | 61 | 19 | 60 | 20 | 72 | 93 | 48 | 98 | 57 | 07 | 23 | 69 | 65 | 95 | 39 | 69 | 58 | 56 | 80 | 30 | 19 | 44 |
| 25 | 78 | 60 | 73 | 99 | 84 | 43 | 89 | 94 | 36 | 45 | 56 | 69 | 47 | 07 | 41 | 90 | 22 | 91 | 07 | 12 | 78 | 35 | 34 | 08 | 72 |
| 26 | 84 | 37 | 90 | 61 | 56 | 70 | 10 | 23 | 98 | 05 | 85 | 11 | 34 | 76 | 60 | 76 | 48 | 45 | 34 | 60 | 01 | 64 | 18 | 39 | 96 |
| 27 | 36 | 67 | 10 | 08 | 23 | 98 | 93 | 35 | 08 | 86 | 99 | 29 | 76 | 29 | 81 | 33 | 34 | 91 | 58 | 93 | 63 | 14 | 52 | 32 | 52 |
| 28 | 07 | 28 | 59 | 07 | 48 | 89 | 64 | 58 | 89 | 75 | 83 | 85 | 62 | 27 | 89 | 30 | 14 | 78 | 56 | 27 | 86 | 63 | 59 | 80 | 02 |
| 29 | 10 | 15 | 83 | 87 | 60 | 79 | 24 | 31 | 66 | 56 | 21 | 48 | 24 | 06 | 93 | 91 | 98 | 94 | 05 | 49 | 01 | 47 | 59 | 38 | 00 |
| 30 | 55 | 19 | 68 | 97 | 65 | 03 | 73 | 52 | 16 | 56 | 00 | 53 | 55 | 90 | 27 | 33 | 42 | 29 | 38 | 87 | 22 | 13 | 88 | 83 | 34 |
| 31 | 53 | 81 | 29 | 13 | 39 | 35 | 01 | 20 | 71 | 34 | 62 | 33 | 74 | 82 | 14 | 53 | 73 | 19 | 09 | 03 | 56 | 54 | 29 | 56 | 93 |
| 32 | 51 | 86 | 32 | 68 | 92 | 33 | 98 | 74 | 66 | 99 | 40 | 14 | 71 | 94 | 58 | 45 | 94 | 19 | 38 | 81 | 14 | 44 | 99 | 81 | 07 |
| 33 | 35 | 91 | 70 | 29 | 13 | 80 | 03 | 54 | 07 | 27 | 96 | 94 | 78 | 32 | 66 | 50 | 95 | 52 | 74 | 33 | 13 | 80 | 55 | 62 | 54 |
| 34 | 37 | 71 | 67 | 95 | 13 | 20 | 02 | 44 | 95 | 94 | 64 | 85 | 04 | 05 | 72 | 01 | 32 | 90 | 76 | 14 | 53 | 89 | 74 | 60 | 41 |
| 35 | 93 | 66 | 13 | 83 | 27 | 92 | 79 | 64 | 64 | 72 | 28 | 54 | 96 | 53 | 84 | 48 | 14 | 52 | 98 | 94 | 56 | 07 | 93 | 89 | 30 |
| 36 | 02 | 96 | 08 | 45 | 65 | 13 | 05 | 00 | 41 | 84 | 93 | 07 | 54 | 72 | 59 | 21 | 45 | 57 | 09 | 77 | 19 | 48 | 56 | 27 | 44 |
| 37 | 49 | 83 | 43 | 48 | 35 | 82 | 88 | 33 | 69 | 96 | 72 | 36 | 04 | 19 | 76 | 47 | 45 | 15 | 18 | 60 | 82 | 11 | 08 | 95 | 97 |
| 38 | 84 | 60 | 71 | 62 | 46 | 40 | 80 | 81 | 30 | 37 | 34 | 39 | 23 | 05 | 38 | 25 | 15 | 35 | 71 | 30 | 88 | 12 | 57 | 21 | 77 |
| 39 | 18 | 17 | 30 | 88 | 71 | 44 | 91 | 14 | 88 | 47 | 89 | 23 | 30 | 63 | 15 | 56 | 34 | 20 | 47 | 89 | 99 | 82 | 93 | 24 | 98 |
| 40 | 79 | 69 | 10 | 61 | 78 | 71 | 32 | 76 | 95 | 62 | 87 | 00 | 22 | 58 | 40 | 92 | 54 | 01 | 75 | 25 | 43 | 11 | 71 | 99 | 31 |
| 41 | 75 | 93 | 36 | 57 | 83 | 56 | 20 | 14 | 82 | 11 | 74 | 21 | 97 | 90 | 65 | 96 | 42 | 68 | 63 | 86 | 74 | 54 | 13 | 26 | 94 |
| 42 | 38 | 30 | 92 | 29 | 03 | 06 | 28 | 81 | 39 | 38 | 62 | 25 | 06 | 84 | 63 | 61 | 29 | 08 | 93 | 67 | 04 | 32 | 92 | 08 | 09 |
| 43 | 51 | 29 | 50 | 10 | 34 | 31 | 57 | 75 | 95 | 80 | 51 | 97 | 02 | 74 | 77 | 76 | 15 | 48 | 49 | 44 | 18 | 55 | 63 | 77 | 09 |
| 44 | 21 | 31 | 38 | 86 | 24 | 37 | 79 | 81 | 53 | 74 | 73 | 24 | 16 | 10 | 33 | 52 | 83 | 90 | 94 | 76 | 70 | 47 | 14 | 54 | 36 |
| 45 | 29 | 01 | 23 | 87 | 82 | 58 | 02 | 39 | 37 | 67 | 42 | 10 | 14 | 20 | 92 | 16 | 55 | 23 | 42 | 45 | 54 | 96 | 09 | 11 | 06 |
| 46 | 95 | 33 | 95 | 22 | 00 | 18 | 74 | 72 | 00 | 18 | 38 | 79 | 58 | 69 | 32 | 81 | 76 | 80 | 26 | 92 | 82 | 80 | 84 | 25 | 39 |
| 47 | 90 | 84 | 60 | 79 | 80 | 24 | 36 | 59 | 87 | 38 | 82 | 07 | 53 | 89 | 35 | 96 | 35 | 23 | 79 | 18 | 05 | 98 | 90 | 07 | 35 |
| 48 | 46 | 40 | 62 | 98 | 82 | 54 | 97 | 20 | 56 | 95 | 15 | 74 | 80 | 08 | 32 | 16 | 46 | 70 | 50 | 80 | 67 | 72 | 16 | 42 | 79 |
| 49 | 20 | 31 | 89 | 03 | 43 | 38 | 46 | 82 | 68 | 72 | 32 | 14 | 82 | 99 | 70 | 80 | 60 | 47 | 18 | 97 | 63 | 49 | 30 | 21 | 30 |
| 50 | 71 | 59 | 73 | 05 | 50 | 08 | 22 | 23 | 71 | 77 | 91 | 01 | 93 | 20 | 49 | 82 | 96 | 59 | 26 | 94 | 66 | 39 | 67 | 98 | 60 |
附表 17(3) 随机数字表
| 编号 | 1 | 2 | 3 | 5 | 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 1 | 22 | 17 | 68 | 65 | 84 | 68 | 95 | 23 | 92 | 35 | 87 | 02 | 22 | 57 | 51 | 61 | 09 | 43 | 95 | 06 | 58 | 24 | 82 | 03 | 47 |
| 2 | 19 | 36 | 27 | 59 | 46 | 13 | 79 | 93 | 37 | 55 | 39 | 77 | 32 | 77 | 09 | 85 | 52 | 05 | 30 | 62 | 47 | 83 | 51 | 62 | 74 |
| 3 | 16 | 77 | 23 | 02 | 77 | 09 | 61 | 87 | 25 | 21 | 28 | 06 | 24 | 25 | 93 | 16 | 71 | 13 | 59 | 78 | 23 | 05 | 47 | 47 | 25 |
| 4 | 78 | 43 | 76 | 71 | 61 | 20 | 44 | 90 | 32 | 64 | 97 | 67 | 63 | 99 | 61 | 46 | 38 | 03 | 93 | 22 | 69 | 81 | 21 | 99 | 21 |
| 5 | 03 | 28 | 28 | 26 | 08 | 73 | 37 | 32 | 04 | 05 | 69 | 30 | 16 | 09 | 05 | 88 | 69 | 58 | 28 | 99 | 35 | 07 | 44 | 75 | 47 |
| 6 | 93 | 22 | 53 | 64 | 39 | 07 | 10 | 63 | 76 | 35 | 87 | 03 | 04 | 79 | 88 | 08 | 13 | 13 | 85 | 51 | 55 | 34 | 57 | 72 | 69 |
| 7 | 78 | 76 | 58 | 54 | 74 | 92 | 38 | 70 | 96 | 92 | 52 | 06 | 79 | 79 | 45 | 82 | 63 | 18 | 27 | 44 | 69 | 66 | 92 | 19 | 09 |
| 8 | 23 | 68 | 35 | 26 | 00 | 99 | 53 | 93 | 61 | 28 | 52 | 70 | 05 | 48 | 34 | 56 | 65 | 05 | 61 | 86 | 90 | 92 | 10 | 70 | 80 |
| 9 | 15 | 39 | 25 | 70 | 99 | 93 | 86 | 52 | 77 | 65 | 15 | 33 | 59 | 05 | 28 | 22 | 87 | 26 | 07 | 47 | 86 | 96 | 98 | 29 | 06 |
| 10 | 58 | 71 | 96 | 30 | 24 | 18 | 46 | 23 | 34 | 27 | 85 | 13 | 99 | 24 | 44 | 49 | 18 | 09 | 79 | 49 | 74 | 16 | 32 | 23 | 02 |
| 11 | 57 | 35 | 27 | 33 | 72 | 24 | 53 | 63 | 94 | 09 | 41 | 10 | 76 | 47 | 91 | 44 | 04 | 95 | 49 | 66 | 39 | 60 | 04 | 59 | 81 |
| 12 | 48 | 50 | 86 | 54 | 48 | 22 | 06 | 34 | 72 | 52 | 82 | 21 | 15 | 65 | 20 | 33 | 29 | 94 | 71 | 11 | 15 | 91 | 29 | 12 | 03 |
| 13 | 61 | 96 | 48 | 95 | 03 | 07 | 16 | 39 | 33 | 66 | 98 | 56 | 10 | 56 | 79 | 77 | 21 | 30 | 27 | 12 | 90 | 49 | 22 | 23 | 62 |
| 14 | 36 | 93 | 89 | 41 | 26 | 29 | 70 | 83 | 63 | 51 | 99 | 74 | 20 | 52 | 36 | 87 | 09 | 41 | 15 | 09 | 98 | 60 | 16 | 03 | 03 |
| 15 | 18 | 87 | 00 | 42 | 31 | 57 | 90 | 12 | 02 | 07 | 23 | 47 | 37 | 17 | 31 | 54 | 08 | 01 | 88 | 63 | 39 | 41 | 88 | 92 | 10 |
| 16 | 88 | 56 | 53 | 27 | 59 | 33 | 35 | 72 | 67 | 47 | 77 | 34 | 55 | 45 | 70 | 08 | 18 | 27 | 38 | 90 | 16 | 95 | 86 | 70 | 75 |
| 17 | 09 | 72 | 95 | 84 | 29 | 49 | 41 | 31 | 06 | 70 | 42 | 38 | 06 | 45 | 18 | 64 | 84 | 73 | 31 | 65 | 52 | 53 | 37 | 97 | 15 |
| 18 | 12 | 96 | 88 | 17 | 31 | 65 | 19 | 69 | 02 | 83 | 60 | 75 | 86 | 90 | 68 | 24 | 64 | 19 | 35 | 51 | 56 | 61 | 87 | 39 | 12 |
| 19 | 85 | 94 | 57 | 24 | 16 | 92 | 09 | 84 | 38 | 76 | 22 | 00 | 27 | 69 | 85 | 29 | 81 | 94 | 78 | 70 | 21 | 94 | 47 | 90 | 12 |
| 20 | 38 | 64 | 43 | 59 | 93 | 98 | 77 | 87 | 68 | 07 | 91 | 51 | 67 | 62 | 44 | 40 | 98 | 05 | 93 | 78 | 23 | 32 | 65 | 41 | 18 |
| 21 | 53 | 44 | 09 | 42 | 72 | 00 | 41 | 86 | 79 | 79 | 68 | 47 | 22 | 00 | 20 | 35 | 55 | 31 | 51 | 51 | 00 | 83 | 63 | 22 | 55 |
| 22 | 40 | 76 | 66 | 26 | 84 | 57 | 99 | 99 | 90 | 37 | 36 | 63 | 32 | 08 | 58 | 37 | 40 | 13 | 68 | 97 | 87 | 64 | 81 | 07 | 83 |
| 23 | 02 | 17 | 79 | 18 | 05 | 12 | 59 | 52 | 57 | 02 | 22 | 07 | 90 | 47 | 03 | 28 | 14 | 11 | 30 | 79 | 20 | 69 | 22 | 40 | 98 |
| 24 | 95 | 17 | 82 | 06 | 53 | 31 | 51 | 10 | 96 | 46 | 92 | 06 | 88 | 07 | 77 | 56 | 11 | 50 | 81 | 69 | 40 | 23 | 72 | 51 | 39 |
| 25 | 35 | 76 | 22 | 42 | 92 | 96 | 11 | 83 | 44 | 80 | 34 | 68 | 35 | 48 | 77 | 33 | 42 | 40 | 90 | 60 | 73 | 96 | 53 | 97 | 86 |
| 26 | 26 | 29 | 13 | 56 | 41 | 85 | 47 | 04 | 66 | 08 | 34 | 72 | 57 | 59 | 13 | 82 | 43 | 80 | 46 | 15 | 38 | 26 | 61 | 70 | 04 |
| 27 | 77 | 80 | 20 | 75 | 82 | 72 | 82 | 32 | 99 | 90 | 63 | 95 | 73 | 76 | 63 | 89 | 73 | 44 | 99 | 05 | 48 | 67 | 26 | 43 | 13 |
| 28 | 46 | 40 | 66 | 44 | 52 | 91 | 36 | 74 | 43 | 53 | 30 | 82 | 13 | 54 | 00 | 78 | 45 | 63 | 98 | 35 | 55 | 03 | 36 | 67 | 68 |
| 29 | 37 | 56 | 08 | 18 | 09 | 77 | 53 | 84 | 46 | 47 | 31 | 91 | 18 | 95 | 58 | 24 | 16 | 74 | 11 | 53 | 44 | 10 | 13 | 85 | 57 |
| 30 | 61 | 65 | 61 | 68 | 66 | 37 | 27 | 47 | 39 | 19 | 84 | 83 | 70 | 07 | 48 | 53 | 21 | 40 | 06 | 71 | 95 | 06 | 79 | 88 | 54 |
| 31 | 93 | 43 | 69 | 64 | 07 | 34 | 18 | 04 | 52 | 35 | 56 | 27 | 09 | 24 | 86 | 61 | 85 | 53 | 83 | 45 | 19 | 90 | 70 | 99 | 00 |
| 32 | 21 | 96 | 60 | 12 | 99 | 11 | 20 | 99 | 45 | 18 | 48 | 13 | 93 | 55 | 34 | 18 | 37 | 79 | 49 | 90 | 65 | 97 | 38 | 20 | 46 |
| 33 | 95 | 20 | 47 | 97 | 97 | 27 | 37 | 83 | 28 | 71 | 00 | 06 | 41 | 41 | 74 | 45 | 80 | 09 | 39 | 84 | 51 | 67 | 11 | 52 | 49 |
| 34 | 97 | 86 | 21 | 78 | 73 | 10 | 65 | 81 | 92 | 59 | 58 | 76 | 17 | 14 | 97 | 04 | 76 | 62 | 16 | 17 | 17 | 95 | 70 | 45 | 80 |
| 35 | 69 | 92 | 06 | 34 | 13 | 59 | 71 | 74 | 17 | 32 | 27 | 55 | 10 | 24 | 19 | 23 | 71 | 82 | 13 | 74 | 63 | 52 | 52 | 01 | 41 |
| 36 | 04 | 31 | 17 | 21 | 56 | 33 | 73 | 99 | 19 | 87 | 26 | 72 | 39 | 27 | 67 | 53 | 77 | 57 | 68 | 93 | 60 | 61 | 97 | 22 | 61 |
| 37 | 61 | 06 | 98 | 03 | 91 | 87 | 14 | 77 | 43 | 96 | 43 | 00 | 65 | 98 | 50 | 45 | 60 | 33 | 01 | 07 | 98 | 99 | 46 | 50 | 47 |
| 38 | 85 | 93 | 85 | 86 | 88 | 72 | 87 | 08 | 62 | 40 | 16 | 06 | 10 | 89 | 20 | 23 | 21 | 34 | 74 | 97 | 76 | 38 | 03 | 29 | 63 |
| 39 | 21 | 74 | 32 | 47 | 45 | 73 | 96 | 07 | 94 | 52 | 09 | 65 | 90 | 77 | 47 | 25 | 76 | 16 | 19 | 33 | 53 | 05 | 70 | 53 | 30 |
| 40 | 15 | 69 | 53 | 82 | 80 | 79 | 96 | 23 | 53 | 10 | 65 | 39 | 07 | 16 | 29 | 45 | 33 | 02 | 43 | 70 | 02 | 87 | 40 | 41 | 45 |
| 41 | 02 | 89 | 08 | 04 | 49 | 20 | 21 | 14 | 68 | 86 | 87 | 63 | 93 | 95 | 17 | 11 | 29 | 01 | 95 | 80 | 35 | 14 | 97 | 35 | 33 |
| 42 | 87 | 18 | 15 | 89 | 79 | 85 | 43 | 01 | 72 | 73 | 08 | 61 | 74 | 51 | 69 | 89 | 74 | 39 | 82 | 15 | 94 | 51 | 33 | 41 | 67 |
| 43 | 98 | 83 | 71 | 94 | 22 | 59 | 97 | 50 | 99 | 52 | 08 | 52 | 85 | 08 | 40 | 87 | 80 | 61 | 65 | 31 | 91 | 51 | 80 | 32 | 44 |
| 44 | 10 | 08 | 58 | 21 | 66 | 72 | 68 | 49 | 29 | 31 | 89 | 85 | 84 | 46 | 06 | 59 | 73 | 19 | 85 | 23 | 65 | 09 | 29 | 75 | 63 |
| 45 | 47 | 90 | 56 | 10 | 08 | 88 | 02 | 84 | 27 | 83 | 42 | 29 | 72 | 23 | 19 | 66 | 56 | 45 | 65 | 79 | 20 | 71 | 53 | 20 | 25 |
| 46 | 22 | 85 | 61 | 68 | 90 | 49 | 64 | 92 | 85 | 44 | 16 | 40 | 12 | 89 | 88 | 50 | 14 | 49 | 81 | 06 | 01 | 82 | 77 | 45 | 12 |
| 47 | 67 | 80 | 43 | 79 | 33 | 12 | 83 | 11 | 41 | 16 | 25 | 58 | 19 | 68 | 70 | 77 | 02 | 54 | 00 | 52 | 53 | 43 | 37 | 15 | 26 |
| 48 | 27 | 62 | 50 | 96 | 72 | 79 | 44 | 61 | 40 | 15 | 14 | 53 | 40 | 65 | 39 | 27 | 31 | 58 | 50 | 28 | 11 | 39 | 03 | 34 | 25 |
| 49 | 33 | 78 | 80 | 87 | 15 | 38 | 30 | 06 | 38 | 21 | 14 | 47 | 47 | 07 | 26 | 54 | 96 | 87 | 53 | 32 | 40 | 36 | 40 | 96 | 76 |
| 50 | 13 | 13 | 92 | 66 | 99 | 47 | 24 | 49 | 57 | 74 | 22 | 25 | 43 | 02 | 17 | 10 | 97 | 11 | 69 | 84 | 99 | 63 | 22 | 32 | 98 |
附表 17(4) 随机数字表
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 23 | 22 | 23 | 24 | 25 |
| 1 | 10 | 27 | 53 | 96 | 23 | 71 | 50 | 54 | 36 | 23 | 54 | 31 | 04 | 82 | 93 | 04 | 14 | 12 | 15 | 09 | 26 | 78 | 25 | 47 | 47 |
| 2 | 28 | 41 | 50 | 61 | 88 | 64 | 85 | 27 | 20 | 18 | 83 | 36 | 36 | 05 | 56 | 39 | 71 | 65 | 09 | 62 | 94 | 76 | 62 | 11 | 89 |
| 3 | 34 | 21 | 42 | 57 | 02 | 59 | 19 | 18 | 97 | 48 | 80 | 30 | 03 | 30 | 98 | 05 | 24 | 67 | 70 | 07 | 84 | 97 | 50 | 87 | 46 |
| 4 | 61 | 81 | 77 | 23 | 23 | 82 | 82 | 11 | 54 | 08 | 53 | 28 | 70 | 58 | 96 | 44 | 07 | 39 | 55 | 43 | 42 | 34 | 43 | 39 | 28 |
| 5 | 61 | 15 | 18 | 13 | 54 | 16 | 86 | 20 | 26 | 88 | 90 | 74 | 80 | 55 | 09 | 14 | 53 | 90 | 51 | 17 | 52 | 01 | 63 | 01 | 59 |
| 6 | 91 | 76 | 21 | 64 | 64 | 44 | 91 | 13 | 32 | 97 | 75 | 31 | 62 | 66 | 54 | 84 | 80 | 32 | 75 | 77 | 56 | 08 | 25 | 70 | 29 |
| 7 | 00 | 97 | 79 | 08 | 06 | 37 | 30 | 28 | 59 | 85 | 53 | 56 | 68 | 53 | 40 | 01 | 74 | 39 | 59 | 73 | 30 | 19 | 99 | 85 | 48 |
| 8 | 36 | 46 | 18 | 34 | 94 | 75 | 20 | 80 | 27 | 77 | 78 | 91 | 69 | 16 | 00 | 08 | 43 | 18 | 73 | 68 | 67 | 69 | 61 | 34 | 25 |
| 9 | 88 | 98 | 99 | 60 | 50 | 65 | 95 | 79 | 42 | 94 | 93 | 62 | 40 | 89 | 96 | 43 | 56 | 47 | 71 | 66 | 46 | 76 | 29 | 67 | 02 |
| 10 | 04 | 37 | 59 | 87 | 21 | 05 | 02 | 03 | 24 | 17 | 47 | 97 | 81 | 56 | 51 | 92 | 34 | 86 | 01 | 82 | 55 | 51 | 33 | 12 | 91 |
| 11 | 63 | 62 | 06 | 34 | 41 | 94 | 21 | 78 | 55 | 09 | 72 | 76 | 45 | 16 | 94 | 29 | 95 | 81 | 83 | 83 | 79 | 88 | 01 | 97 | 30 |
| 12 | 78 | 47 | 23 | 53 | 90 | 34 | 41 | 92 | 45 | 71 | 09 | 23 | 70 | 70 | 07 | 12 | 38 | 92 | 79 | 43 | 14 | 85 | 11 | 47 | 23 |
| 13 | 87 | 68 | 62 | 15 | 43 | 53 | 14 | 36 | 59 | 25 | 54 | 47 | 33 | 70 | 15 | 59 | 24 | 48 | 40 | 35 | 50 | 03 | 42 | 99 | 36 |
| 14 | 47 | 60 | 92 | 10 | 77 | 88 | 59 | 53 | 11 | 52 | 66 | 25 | 69 | 07 | 04 | 48 | 68 | 64 | 71 | 06 | 61 | 65 | 70 | 22 | 12 |
| 15 | 56 | 88 | 87 | 59 | 41 | 65 | 28 | 04 | 67 | 53 | 95 | 79 | 88 | 37 | 31 | 50 | 41 | 06 | 94 | 76 | 81 | 83 | 17 | 16 | 33 |
| 16 | 02 | 57 | 45 | 86 | 67 | 73 | 43 | 07 | 34 | 48 | 44 | 26 | 87 | 93 | 29 | 77 | 09 | 61 | 67 | 84 | 06 | 69 | 44 | 77 | 75 |
| 17 | 31 | 54 | 14 | 13 | 17 | 48 | 62 | 11 | 90 | 60 | 68 | 12 | 93 | 64 | 28 | 46 | 24 | 79 | 16 | 76 | 14 | 60 | 25 | 51 | 01 |
| 18 | 28 | 50 | 16 | 43 | 36 | 28 | 97 | 85 | 58 | 99 | 67 | 22 | 52 | 76 | 23 | 24 | 70 | 36 | 54 | 54 | 59 | 28 | 61 | 71 | 96 |
| 19 | 53 | 29 | 62 | 66 | 50 | 02 | 63 | 45 | 52 | 38 | 67 | 63 | 47 | 54 | 75 | 83 | 24 | 78 | 43 | 20 | 92 | 63 | 13 | 47 | 48 |
| 20 | 45 | 65 | 58 | 26 | 51 | 76 | 96 | 59 | 38 | 72 | 86 | 57 | 45 | 71 | 46 | 44 | 67 | 76 | 14 | 55 | 44 | 88 | 01 | 62 | 12 |
| 21 | 39 | 65 | 36 | 63 | 70 | 77 | 45 | 85 | 50 | 51 | 74 | 13 | 39 | 35 | 22 | 30 | 53 | 36 | 02 | 95 | 49 | 34 | 88 | 73 | 61 |
| 22 | 73 | 71 | 98 | 16 | 04 | 29 | 18 | 94 | 51 | 23 | 76 | 51 | 94 | 84 | 86 | 79 | 93 | 96 | 38 | 63 | 08 | 58 | 25 | 58 | 94 |
| 23 | 72 | 20 | 56 | 20 | 11 | 72 | 65 | 71 | 08 | 86 | 79 | 57 | 95 | 13 | 91 | 97 | 48 | 72 | 66 | 48 | 09 | 71 | 17 | 24 | 96 |
| 24 | 75 | 17 | 26 | 99 | 76 | 89 | 37 | 20 | 70 | 01 | 77 | 31 | 61 | 95 | 46 | 26 | 97 | 05 | 73 | 51 | 53 | 33 | 18 | 72 | 87 |
| 25 | 37 | 48 | 60 | 82 | 29 | 81 | 30 | 15 | 39 | 14 | 48 | 38 | 75 | 93 | 29 | 06 | 87 | 37 | 78 | 48 | 45 | 46 | 00 | 84 | 47 |
| 26 | 68 | 08 | 02 | 80 | 72 | 83 | 71 | 46 | 30 | 49 | 89 | 17 | 95 | 88 | 29 | 02 | 39 | 56 | 03 | 46 | 97 | 74 | 06 | 56 | 17 |
| 27 | 14 | 23 | 98 | 61 | 67 | 70 | 52 | 85 | 01 | 50 | 01 | 84 | 02 | 78 | 43 | 10 | 62 | 98 | 19 | 41 | 18 | 83 | 99 | 47 | 99 |
| 28 | 49 | 08 | 96 | 21 | 44 | 25 | 27 | 99 | 41 | 28 | 07 | 41 | 08 | 34 | 66 | 19 | 42 | 74 | 39 | 91 | 41 | 96 | 53 | 78 | 72 |
| 29 | 78 | 37 | 06 | 08 | 43 | 63 | 61 | 62 | 42 | 29 | 39 | 68 | 95 | 10 | 96 | 09 | 24 | 23 | 00 | 62 | 56 | 12 | 80 | 73 | 16 |
| 30 | 37 | 21 | 34 | 17 | 68 | 68 | 96 | 83 | 23 | 56 | 32 | 84 | 60 | 15 | 31 | 44 | 73 | 67 | 34 | 77 | 91 | 15 | 79 | 74 | 58 |
| 31 | 14 | 20 | 09 | 34 | 04 | 87 | 83 | 07 | 55 | 07 | 76 | 58 | 30 | 83 | 64 | 87 | 29 | 25 | 58 | 84 | 86 | 50 | 60 | 00 | 25 |
| 32 | 58 | 43 | 28 | 06 | 36 | 49 | 52 | 83 | 51 | 14 | 47 | 56 | 91 | 29 | 34 | 05 | 87 | 31 | 06 | 95 | 12 | 45 | 47 | 09 | 09 |
| 33 | 10 | 43 | 67 | 29 | 70 | 80 | 62 | 80 | 03 | 42 | 10 | 80 | 21 | 38 | 84 | 90 | 56 | 35 | 03 | 09 | 43 | 12 | 74 | 49 | 14 |
| 34 | 44 | 38 | 88 | 39 | 54 | 86 | 97 | 37 | 44 | 22 | 00 | 95 | 01 | 31 | 76 | 17 | 16 | 29 | 56 | 63 | 38 | 78 | 94 | 49 | 81 |
| 35 | 90 | 69 | 59 | 19 | 51 | 85 | 39 | 52 | 85 | 13 | 07 | 28 | 37 | 07 | 61 | 11 | 16 | 36 | 27 | 03 | 78 | 86 | 72 | 04 | 95 |
| 36 | 41 | 47 | 10 | 25 | 62 | 97 | 05 | 31 | 03 | 61 | 20 | 26 | 36 | 19 | 62 | 68 | 69 | 86 | 95 | 44 | 84 | 95 | 48 | 46 | 45 |
| 37 | 91 | 94 | 14 | 63 | 19 | 75 | 89 | 11 | 47 | 11 | 31 | 56 | 34 | 19 | 09 | 79 | 57 | 92 | 36 | 59 | 14 | 93 | 87 | 81 | 40 |
| 38 | 80 | 06 | 54 | 18 | 66 | 09 | 18 | 94 | 06 | 19 | 98 | 40 | 07 | 17 | 81 | 22 | 45 | 44 | 84 | 11 | 24 | 62 | 20 | 42 | 31 |
| 39 | 67 | 72 | 77 | 63 | 48 | 84 | 08 | 31 | 55 | 58 | 24 | 33 | 45 | 77 | 58 | 80 | 45 | 67 | 93 | 82 | 75 | 70 | 16 | 08 | 24 |
| 40 | 59 | 40 | 24 | 13 | 27 | 79 | 26 | 88 | 86 | 30 | 01 | 31 | 60 | 10 | 39 | 53 | 58 | 47 | 70 | 93 | 85 | 81 | 56 | 39 | 38 |
| 41 | 05 | 90 | 35 | 89 | 95 | 01 | 61 | 16 | 96 | 94 | 50 | 78 | 13 | 69 | 36 | 37 | 68 | 53 | 37 | 31 | 71 | 26 | 35 | 03 | 71 |
| 42 | 44 | 43 | 80 | 69 | 98 | 46 | 68 | 05 | 14 | 82 | 90 | 78 | 50 | 05 | 62 | 77 | 79 | 13 | 57 | 44 | 59 | 60 | 10 | 39 | 66 |
| 43 | 61 | 81 | 31 | 96 | 82 | 00 | 57 | 25 | 60 | 59 | 46 | 72 | 60 | 18 | 77 | 55 | 66 | 12 | 62 | 11 | 08 | 99 | 55 | 64 | 57 |
| 44 | 42 | 88 | 07 | 10 | 05 | 24 | 98 | 65 | 63 | 21 | 47 | 21 | 61 | 88 | 32 | 27 | 80 | 30 | 21 | 60 | 10 | 92 | 35 | 36 | 12 |
| 45 | 77 | 94 | 30 | 05 | 39 | 28 | 10 | 99 | 00 | 27 | 12 | 73 | 73 | 99 | 12 | 49 | 99 | 57 | 94 | 82 | 96 | 88 | 57 | 17 | 91 |
| 46 | 78 | 83 | 19 | 76 | 16 | 94 | 11 | 68 | 84 | 26 | 23 | 54 | 20 | 86 | 85 | 23 | 86 | 66 | 99 | 07 | 36 | 37 | 34 | 92 | 09 |
| 47 | 87 | 76 | 59 | 61 | 81 | 43 | 63 | 64 | 61 | 61 | 65 | 76 | 36 | 95 | 90 | 18 | 48 | 27 | 45 | 68 | 27 | 23 | 65 | 30 | 72 |
| 48 | 91 | 43 | 05 | 96 | 47 | 55 | 78 | 99 | 95 | 24 | 37 | 55 | 85 | 78 | 78 | 01 | 48 | 41 | 19 | 10 | 35 | 19 | 54 | 07 | 73 |
| 49 | 84 | 97 | 77 | 72 | 73 | 09 | 62 | 06 | 65 | 72 | 37 | 12 | 49 | 03 | 60 | 41 | 15 | 20 | 76 | 27 | 50 | 47 | 02 | 29 | 16 |
| 50 | 87 | 41 | 60 | 76 | 83 | 44 | 88 | 96 | 07 | 80 | 83 | 05 | 83 | 88 | 96 | 73 | 70 | 66 | 81 | 90 | 30 | 56 | 10 | 48 | 59 |
附表 17(5) 随机数字表
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 1 | 28 | 89 | 65 | 87 | 08 | 13 | 50 | 63 | 04 | 23 | 25 | 47 | 57 | 91 | 13 | 52 | 62 | 24 | 19 | 94 | 91 | 67 | 48 | 57 | 10 |
| 2 | 30 | 29 | 43 | 65 | 42 | 78 | 66 | 28 | 55 | 80 | 47 | 46 | 41 | 90 | 08 | 55 | 98 | 78 | 10 | 70 | 49 | 92 | 05 | 12 | 07 |
| 3 | 95 | 74 | 62 | 60 | 53 | 51 | 57 | 32 | 22 | 27 | 12 | 72 | 72 | 27 | 77 | 44 | 67 | 32 | 23 | 13 | 67 | 95 | 07 | 76 | 30 |
| 4 | 01 | 85 | 54 | 96 | 72 | 66 | 86 | 65 | 64 | 60 | 56 | 59 | 75 | 36 | 75 | 46 | 44 | 33 | 63 | 71 | 54 | 50 | 06 | 44 | 75 |
| 5 | 10 | 91 | 46 | 96 | 86 | 19 | 83 | 52 | 47 | 53 | 65 | 00 | 51 | 93 | 51 | 30 | 80 | 05 | 19 | 29 | 56 | 23 | 27 | 19 | 03 |
| 6 | 05 | 33 | 18 | 08 | 51 | 51 | 78 | 57 | 26 | 17 | 34 | 87 | 96 | 23 | 95 | 89 | 99 | 93 | 39 | 79 | 11 | 28 | 94 | 15 | 52 |
| 7 | 04 | 43 | 13 | 37 | 00 | 79 | 68 | 96 | 26 | 60 | 70 | 39 | 83 | 66 | 56 | 62 | 03 | 55 | 86 | 57 | 77 | 55 | 33 | 62 | 02 |
| 8 | 05 | 85 | 40 | 25 | 24 | 73 | 52 | 93 | 70 | 50 | 48 | 21 | 47 | 74 | 63 | 17 | 27 | 27 | 51 | 26 | 35 | 96 | 29 | 00 | 45 |
| 9 | 84 | 90 | 90 | 65 | 77 | 63 | 99 | 25 | 69 | 02 | 09 | 04 | 03 | 35 | 78 | 19 | 79 | 95 | 07 | 21 | 02 | 84 | 48 | 51 | 97 |
| 10 | 28 | 55 | 53 | 09 | 48 | 86 | 28 | 30 | 02 | 35 | 71 | 30 | 32 | 06 | 47 | 93 | 74 | 21 | 86 | 33 | 49 | 90 | 21 | 69 | 74 |
| 11 | 89 | 83 | 40 | 69 | 80 | 97 | 96 | 47 | 59 | 97 | 56 | 33 | 24 | 87 | 36 | 17 | 18 | 16 | 90 | 46 | 75 | 27 | 28 | 52 | 13 |
| 12 | 73 | 20 | 96 | 05 | 68 | 93 | 41 | 69 | 96 | 07 | 97 | 50 | 81 | 79 | 59 | 42 | 37 | 13 | 81 | 83 | 92 | 42 | 85 | 04 | 31 |
| 13 | 10 | 89 | 07 | 76 | 21 | 40 | 24 | 74 | 36 | 42 | 40 | 33 | 04 | 46 | 24 | 35 | 63 | 02 | 31 | 61 | 34 | 59 | 43 | 36 | 96 |
| 14 | 91 | 50 | 27 | 78 | 37 | 06 | 06 | 16 | 25 | 98 | 17 | 78 | 80 | 36 | 85 | 26 | 41 | 77 | 63 | 37 | 71 | 63 | 94 | 94 | 33 |
| 15 | 03 | 45 | 44 | 66 | 88 | 97 | 81 | 26 | 03 | 89 | 39 | 46 | 67 | 21 | 17 | 98 | 10 | 39 | 33 | 15 | 61 | 63 | 00 | 25 | 92 |
| 16 | 89 | 41 | 58 | 91 | 63 | 65 | 99 | 59 | 97 | 84 | 90 | 14 | 79 | 61 | 55 | 56 | 16 | 88 | 87 | 60 | 32 | 15 | 99 | 67 | 43 |
| 17 | 13 | 43 | 00 | 97 | 26 | 16 | 91 | 21 | 32 | 41 | 60 | 22 | 66 | 72 | 17 | 31 | 85 | 33 | 69 | 07 | 68 | 49 | 20 | 43 | 29 |
| 18 | 71 | 71 | 00 | 51 | 72 | 62 | 03 | 89 | 26 | 32 | 35 | 27 | 99 | 18 | 25 | 78 | 12 | 03 | 09 | 70 | 50 | 93 | 19 | 35 | 56 |
| 19 | 19 | 28 | 15 | 00 | 41 | 92 | 27 | 73 | 40 | 38 | 37 | 11 | 05 | 75 | 16 | 98 | 81 | 99 | 37 | 29 | 92 | 20 | 32 | 39 | 67 |
| 20 | 56 | 38 | 30 | 92 | 30 | 45 | 51 | 94 | 69 | 04 | 00 | 84 | 14 | 36 | 37 | 95 | 66 | 39 | 01 | 09 | 21 | 68 | 40 | 95 | 79 |
| 21 | 39 | 27 | 52 | 89 | 11 | 00 | 81 | 06 | 28 | 48 | 12 | 08 | 05 | 75 | 26 | 03 | 35 | 63 | 05 | 77 | 13 | 81 | 20 | 67 | 58 |
| 22 | 73 | 13 | 28 | 58 | 01 | 05 | 06 | 42 | 24 | 07 | 60 | 60 | 29 | 99 | 93 | 72 | 93 | 78 | 04 | 36 | 05 | 76 | 01 | 54 | 03 |
| 23 | 81 | 60 | 84 | 51 | 57 | 12 | 68 | 46 | 55 | 89 | 60 | 09 | 71 | 87 | 89 | 70 | 81 | 10 | 95 | 91 | 83 | 79 | 68 | 20 | 66 |
| 24 | 05 | 62 | 98 | 07 | 85 | 07 | 79 | 26 | 69 | 61 | 67 | 85 | 72 | 37 | 41 | 85 | 79 | 76 | 48 | 23 | 61 | 58 | 87 | 08 | 05 |
| 25 | 62 | 97 | 16 | 29 | 18 | 52 | 16 | 16 | 23 | 56 | 62 | 95 | 80 | 97 | 63 | 32 | 25 | 34 | 03 | 36 | 48 | 84 | 60 | 37 | 65 |
| 26 | 31 | 13 | 63 | 21 | 08 | 16 | 01 | 92 | 58 | 21 | 48 | 79 | 74 | 73 | 72 | 08 | 64 | 80 | 91 | 38 | 07 | 28 | 66 | 61 | 59 |
| 27 | 97 | 38 | 35 | 34 | 19 | 89 | 84 | 05 | 34 | 47 | 88 | 09 | 31 | 54 | 88 | 97 | 96 | 86 | 01 | 69 | 46 | 13 | 95 | 65 | 96 |
| 28 | 32 | 11 | 78 | 33 | 82 | 51 | 99 | 98 | 44 | 39 | 12 | 75 | 10 | 60 | 36 | 80 | 66 | 39 | 94 | 97 | 42 | 36 | 31 | 16 | 59 |
| 29 | 81 | 99 | 13 | 37 | 05 | 08 | 12 | 60 | 39 | 23 | 61 | 73 | 84 | 89 | 18 | 26 | 02 | 04 | 37 | 95 | 96 | 18 | 69 | 06 | 30 |
| 30 | 45 | 74 | 00 | 03 | 05 | 69 | 99 | 47 | 26 | 52 | 48 | 06 | 30 | 00 | 18 | 03 | 30 | 28 | 55 | 59 | 66 | 10 | 71 | 44 | 05 |
| 31 | 11 | 84 | 13 | 69 | 01 | 88 | 91 | 28 | 79 | 50 | 71 | 42 | 14 | 96 | 55 | 98 | 59 | 96 | 01 | 36 | 88 | 77 | 90 | 45 | 59 |
| 32 | 14 | 66 | 12 | 87 | 22 | 59 | 45 | 27 | 08 | 51 | 85 | 64 | 23 | 85 | 41 | 64 | 72 | 08 | 59 | 44 | 67 | 98 | 36 | 65 | 56 |
| 33 | 40 | 25 | 67 | 87 | 82 | 84 | 27 | 17 | 30 | 37 | 48 | 69 | 49 | 02 | 58 | 98 | 02 | 50 | 58 | 11 | 95 | 39 | 06 | 35 | 63 |
| 34 | 44 | 48 | 97 | 49 | 43 | 65 | 45 | 53 | 41 | 07 | 14 | 83 | 46 | 74 | 11 | 76 | 66 | 63 | 60 | 08 | 90 | 54 | 33 | 65 | 84 |
| 35 | 41 | 94 | 54 | 06 | 57 | 48 | 28 | 01 | 83 | 84 | 09 | 11 | 21 | 91 | 73 | 97 | 28 | 44 | 74 | 06 | 22 | 30 | 95 | 69 | 72 |
| 36 | 07 | 12 | 15 | 58 | 84 | 93 | 18 | 31 | 83 | 45 | 54 | 52 | 62 | 29 | 91 | 53 | 58 | 54 | 66 | 05 | 47 | 19 | 63 | 92 | 75 |
| 37 | 64 | 27 | 90 | 43 | 52 | 18 | 26 | 32 | 96 | 83 | 50 | 58 | 45 | 27 | 57 | 14 | 96 | 39 | 64 | 85 | 73 | 87 | 96 | 76 | 23 |
| 38 | 80 | 71 | 86 | 41 | 03 | 45 | 62 | 63 | 40 | 88 | 35 | 69 | 34 | 10 | 94 | 32 | 22 | 52 | 04 | 74 | 69 | 63 | 21 | 83 | 41 |
| 39 | 27 | 06 | 08 | 09 | 92 | 26 | 22 | 59 | 28 | 27 | 38 | 58 | 22 | 14 | 79 | 24 | 32 | 12 | 38 | 42 | 33 | 56 | 90 | 92 | 57 |
| 40 | 54 | 68 | 97 | 20 | 54 | 33 | 26 | 74 | 03 | 30 | 74 | 22 | 19 | 13 | 48 | 30 | 28 | 01 | 92 | 49 | 58 | 61 | 52 | 27 | 03 |
| 41 | 02 | 92 | 65 | 68 | 99 | 05 | 53 | 15 | 26 | 70 | 04 | 69 | 22 | 64 | 07 | 04 | 73 | 25 | 74 | 82 | 78 | 35 | 22 | 21 | 88 |
| 42 | 83 | 52 | 57 | 78 | 62 | 98 | 61 | 70 | 48 | 22 | 68 | 50 | 64 | 55 | 75 | 42 | 70 | 32 | 09 | 60 | 58 | 70 | 61 | 43 | 97 |
| 43 | 82 | 82 | 76 | 31 | 33 | 85 | 13 | 41 | 38 | 10 | 16 | 47 | 61 | 43 | 77 | 83 | 27 | 19 | 70 | 41 | 34 | 78 | 77 | 60 | 25 |
| 44 | 38 | 61 | 34 | 09 | 49 | 04 | 41 | 66 | 09 | 76 | 20 | 50 | 73 | 40 | 95 | 24 | 77 | 95 | 73 | 20 | 47 | 42 | 80 | 61 | 03 |
| 45 | 01 | 01 | 11 | 88 | 38 | 03 | 10 | 16 | 82 | 24 | 39 | 58 | 20 | 12 | 39 | 82 | 77 | 02 | 18 | 88 | 33 | 11 | 49 | 15 | 16 |
| 46 | 21 | 66 | 14 | 38 | 28 | 54 | 08 | 18 | 07 | 04 | 92 | 17 | 63 | 36 | 75 | 33 | 14 | 11 | 11 | 78 | 97 | 30 | 53 | 62 | 38 |
| 47 | 32 | 29 | 30 | 69 | 59 | 68 | 50 | 33 | 31 | 47 | 15 | 64 | 88 | 75 | 27 | 04 | 51 | 41 | 61 | 96 | 86 | 62 | 93 | 66 | 71 |
| 48 | 04 | 59 | 21 | 65 | 47 | 39 | 90 | 89 | 86 | 77 | 46 | 86 | 86 | 88 | 86 | 50 | 09 | 13 | 24 | 91 | 54 | 80 | 67 | 78 | 66 |
| 49 | 38 | 64 | 50 | 07 | 36 | 56 | 50 | 45 | 94 | 25 | 48 | 28 | 48 | 30 | 51 | 60 | 73 | 73 | 03 | 87 | 68 | 47 | 37 | 10 | 84 |
| 50 | 48 | 33 | 50 | 83 | 53 | 59 | 77 | 64 | 59 | 90 | 58 | 92 | 62 | 50 | 18 | 93 | 09 | 45 | 89 | 06 | 13 | 26 | 98 | 86 | 29 |
附表 17(6) 随机数字表
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 1 | 25 | 19 | 64 | 82 | 84 | 62 | 74 | 29 | 92 | 24 | 61 | 03 | 91 | 22 | 48 | 64 | 94 | 63 | 15 | 07 | 66 | 85 | 12 | 00 | 27 |
| 2 | 23 | 02 | 41 | 46 | 04 | 44 | 31 | 52 | 43 | 07 | 44 | 06 | 03 | 09 | 34 | 19 | 83 | 94 | 62 | 94 | 48 | 28 | 01 | 51 | 92 |
| 3 | 55 | 85 | 66 | 96 | 28 | 28 | 30 | 62 | 58 | 83 | 65 | 68 | 62 | 42 | 45 | 13 | 08 | 60 | 46 | 28 | 95 | 68 | 45 | 52 | 43 |
| 4 | 68 | 45 | 19 | 69 | 59 | 35 | 14 | 82 | 56 | 80 | 22 | 06 | 52 | 26 | 39 | 59 | 78 | 98 | 76 | 14 | 36 | 09 | 03 | 01 | 86 |
| 5 | 69 | 31 | 46 | 29 | 85 | 18 | 88 | 26 | 95 | 54 | 01 | 02 | 14 | 03 | 05 | 48 | 00 | 26 | 43 | 85 | 33 | 93 | 81 | 15 | 97 |
| 6 | 37 | 31 | 61 | 28 | 98 | 94 | 61 | 47 | 03 | 10 | 67 | 80 | 84 | 41 | 26 | 88 | 84 | 59 | 69 | 14 | 77 | 32 | 82 | 81 | 89 |
| 7 | 66 | 42 | 19 | 24 | 94 | 13 | 13 | 38 | 69 | 96 | 76 | 69 | 76 | 24 | 13 | 43 | 83 | 10 | 13 | 24 | 18 | 32 | 84 | 85 | 04 |
| 8 | 33 | 65 | 78 | 12 | 35 | 91 | 59 | 11 | 38 | 44 | 23 | 31 | 48 | 75 | 74 | 05 | 30 | 08 | 46 | 32 | 90 | 04 | 93 | 56 | 16 |
| 9 | 76 | 32 | 06 | 19 | 35 | 22 | 95 | 30 | 19 | 29 | 57 | 74 | 43 | 20 | 90 | 20 | 25 | 36 | 70 | 69 | 38 | 32 | 11 | 01 | 01 |
| 10 | 43 | 33 | 42 | 02 | 59 | 20 | 39 | 84 | 95 | 61 | 58 | 22 | 04 | 02 | 99 | 99 | 78 | 78 | 83 | 82 | 43 | 67 | 16 | 38 | 95 |
| 11 | 28 | 31 | 93 | 43 | 94 | 87 | 73 | 19 | 38 | 47 | 54 | 36 | 90 | 98 | 10 | 83 | 43 | 32 | 26 | 26 | 22 | 00 | 90 | 59 | 22 |
| 12 | 97 | 19 | 21 | 63 | 34 | 69 | 33 | 17 | 03 | 02 | 11 | 15 | 50 | 46 | 08 | 42 | 69 | 60 | 17 | 42 | 14 | 68 | 61 | 14 | 48 |
| 13 | 82 | 80 | 37 | 14 | 20 | 56 | 39 | 59 | 89 | 63 | 33 | 90 | 38 | 44 | 50 | 78 | 22 | 87 | 10 | 88 | 06 | 58 | 87 | 39 | 67 |
| 14 | 03 | 68 | 03 | 13 | 60 | 64 | 13 | 09 | 37 | 11 | 86 | 02 | 57 | 41 | 99 | 31 | 66 | 60 | 65 | 64 | 03 | 03 | 02 | 58 | 97 |
| 15 | 65 | 16 | 58 | 11 | 01 | 98 | 78 | 80 | 63 | 23 | 07 | 37 | 66 | 20 | 56 | 20 | 96 | 06 | 79 | 80 | 33 | 39 | 40 | 49 | 42 |
| 16 | 24 | 65 | 58 | 57 | 04 | 18 | 62 | 85 | 28 | 24 | 26 | 45 | 17 | 82 | 76 | 39 | 65 | 01 | 73 | 91 | 50 | 37 | 49 | 38 | 73 |
| 17 | 02 | 72 | 64 | 07 | 75 | 85 | 66 | 48 | 38 | 73 | 75 | 10 | 96 | 59 | 31 | 48 | 78 | 00 | 08 | 88 | 72 | 08 | 54 | 57 | 17 |
| 18 | 79 | 16 | 78 | 63 | 99 | 43 | 61 | 00 | 66 | 42 | 76 | 26 | 71 | 14 | 33 | 38 | 86 | 76 | 71 | 65 | 37 | 85 | 05 | 56 | 07 |
| 19 | 04 | 75 | 14 | 93 | 39 | 68 | 52 | 16 | 83 | 34 | 64 | 09 | 44 | 62 | 58 | 48 | 02 | 72 | 26 | 95 | 32 | 67 | 35 | 49 | 71 |
| 20 | 40 | 64 | 64 | 57 | 60 | 97 | 00 | 12 | 91 | 33 | 22 | 14 | 73 | 01 | 11 | 83 | 97 | 68 | 05 | 65 | 67 | 77 | 80 | 98 | 87 |
| 21 | 06 | 27 | 07 | 34 | 26 | 01 | 52 | 48 | 69 | 57 | 19 | 17 | 53 | 55 | 96 | 02 | 41 | 03 | 89 | 33 | 86 | 85 | 73 | 02 | 32 |
| 22 | 62 | 40 | 03 | 87 | 10 | 96 | 88 | 22 | 46 | 94 | 35 | 56 | 60 | 94 | 20 | 60 | 73 | 04 | 84 | 98 | 96 | 41 | 18 | 47 | 07 |
| 23 | 00 | 98 | 48 | 18 | 97 | 91 | 51 | 63 | 27 | 95 | 74 | 25 | 84 | 03 | 07 | 88 | 29 | 04 | 79 | 84 | 03 | 71 | 13 | 78 | 26 |
| 24 | 50 | 61 | 19 | 18 | 91 | 98 | 55 | 83 | 46 | 09 | 49 | 66 | 41 | 12 | 45 | 11 | 49 | 36 | 83 | 43 | 53 | 75 | 35 | 13 | 39 |
| 25 | 38 | 54 | 52 | 25 | 78 | 01 | 98 | 00 | 89 | 85 | 86 | 12 | 22 | 89 | 25 | 10 | 10 | 71 | 19 | 45 | 88 | 54 | 77 | 00 | 07 |
| 26 | 46 | 86 | 80 | 97 | 78 | 65 | 12 | 64 | 64 | 70 | 58 | 41 | 05 | 49 | 08 | 68 | 68 | 88 | 54 | 00 | 81 | 61 | 61 | 80 | 41 |
| 27 | 90 | 72 | 92 | 93 | 10 | 09 | 12 | 81 | 93 | 63 | 69 | 30 | 02 | 04 | 26 | 92 | 26 | 48 | 69 | 45 | 91 | 99 | 08 | 07 | 65 |
| 28 | 66 | 21 | 41 | 77 | 60 | 99 | 35 | 72 | 61 | 22 | 52 | 40 | 74 | 67 | 29 | 97 | 50 | 71 | 39 | 79 | 57 | 82 | 11 | 88 | 06 |
| 29 | 87 | 05 | 46 | 52 | 76 | 89 | 96 | 34 | 22 | 37 | 27 | 11 | 57 | 04 | 19 | 57 | 96 | 08 | 36 | 69 | 07 | 51 | 19 | 92 | 66 |
| 30 | 46 | 90 | 61 | 03 | 06 | 89 | 85 | 33 | 22 | 80 | 34 | 89 | 12 | 29 | 37 | 44 | 71 | 38 | 40 | 37 | 15 | 49 | 55 | 51 | 08 |
| 31 | 11 | 88 | 53 | 06 | 09 | 81 | 83 | 33 | 98 | 29 | 91 | 27 | 59 | 43 | 09 | 70 | 72 | 51 | 49 | 73 | 35 | 97 | 25 | 83 | 41 |
| 32 | 11 | 05 | 92 | 06 | 97 | 68 | 82 | 34 | 08 | 83 | 25 | 40 | 58 | 40 | 64 | 56 | 42 | 78 | 54 | 06 | 60 | 96 | 96 | 12 | 82 |
| 33 | 33 | 94 | 24 | 20 | 28 | 52 | 42 | 07 | 12 | 63 | 34 | 39 | 02 | 92 | 31 | 80 | 61 | 68 | 14 | 19 | 69 | 92 | 14 | 73 | 40 |
| 34 | 24 | 89 | 74 | 75 | 61 | 61 | 02 | 73 | 36 | 85 | 67 | 28 | 50 | 49 | 85 | 37 | 79 | 95 | 02 | 66 | 73 | 19 | 76 | 28 | 13 |
| 35 | 15 | 19 | 74 | 67 | 23 | 61 | 38 | 93 | 73 | 68 | 76 | 23 | 15 | 58 | 20 | 35 | 36 | 82 | 82 | 59 | 01 | 33 | 48 | 17 | 66 |
| 36 | 05 | 64 | 12 | 70 | 88 | 80 | 58 | 35 | 06 | 88 | 73 | 48 | 27 | 39 | 43 | 43 | 40 | 13 | 35 | 45 | 55 | 10 | 54 | 38 | 50 |
| 37 | 57 | 49 | 36 | 44 | 06 | 74 | 93 | 55 | 39 | 26 | 27 | 70 | 98 | 76 | 68 | 78 | 36 | 26 | 24 | 06 | 43 | 24 | 56 | 40 | 80 |
| 38 | 77 | 82 | 96 | 96 | 97 | 60 | 42 | 17 | 18 | 48 | 16 | 34 | 92 | 19 | 52 | 98 | 84 | 48 | 42 | 92 | 83 | 19 | 06 | 77 | 78 |
| 39 | 24 | 10 | 70 | 06 | 51 | 59 | 62 | 37 | 95 | 42 | 53 | 67 | 14 | 95 | 29 | 84 | 65 | 43 | 07 | 30 | 77 | 54 | 00 | 15 | 42 |
| 40 | 50 | 00 | 07 | 78 | 23 | 49 | 54 | 36 | 85 | 14 | 18 | 50 | 54 | 18 | 82 | 23 | 79 | 80 | 71 | 37 | 60 | 62 | 95 | 40 | 30 |
| 41 | 44 | 37 | 76 | 21 | 96 | 37 | 03 | 08 | 98 | 64 | 90 | 85 | 59 | 43 | 64 | 17 | 79 | 96 | 52 | 35 | 21 | 05 | 22 | 59 | 30 |
| 42 | 90 | 57 | 55 | 17 | 47 | 53 | 26 | 79 | 20 | 38 | 69 | 90 | 58 | 64 | 03 | 33 | 48 | 32 | 91 | 54 | 68 | 44 | 90 | 21 | 25 |
| 43 | 50 | 74 | 64 | 67 | 42 | 95 | 28 | 12 | 73 | 23 | 32 | 54 | 98 | 64 | 94 | 82 | 17 | 18 | 17 | 14 | 55 | 16 | 61 | 64 | 29 |
| 44 | 44 | 04 | 70 | 22 | 02 | 84 | 31 | 64 | 64 | 08 | 52 | 55 | 04 | 24 | 29 | 91 | 95 | 43 | 81 | 14 | 66 | 13 | 18 | 47 | 44 |
| 45 | 32 | 74 | 61 | 64 | 73 | 21 | 46 | 51 | 44 | 77 | 72 | 48 | 92 | 00 | 05 | 83 | 59 | 89 | 65 | 06 | 53 | 76 | 70 | 58 | 78 |
| 46 | 75 | 73 | 51 | 70 | 49 | 12 | 53 | 67 | 51 | 54 | 38 | 10 | 11 | 67 | 73 | 22 | 32 | 61 | 43 | 75 | 31 | 61 | 22 | 21 | 11 |
| 47 | 76 | 18 | 36 | 16 | 34 | 16 | 28 | 25 | 82 | 98 | 64 | 26 | 70 | 54 | 87 | 49 | 48 | 55 | 11 | 39 | 91 | 25 | 20 | 80 | 85 |
| 48 | 00 | 17 | 37 | 71 | 81 | 64 | 21 | 91 | 15 | 82 | 81 | 04 | 14 | 52 | 11 | 39 | 07 | 30 | 60 | 77 | 39 | 18 | 27 | 85 | 68 |
| 49 | 54 | 95 | 57 | 55 | 04 | 12 | 77 | 40 | 70 | 11 | 79 | 86 | 61 | 57 | 50 | 52 | 49 | 41 | 73 | 46 | 05 | 63 | 34 | 92 | 33 |
| 50 | 69 | 99 | 95 | 54 | 63 | 44 | 37 | 33 | 53 | 17 | 38 | 06 | 58 | 37 | 93 | 47 | 10 | 62 | 31 | 28 | 63 | 59 | 40 | 40 | 32 |
附表 18(1) 随机化分组表
10×10 随机拉丁方
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | u | rs |
| 1 | 1 | 2 | 7 | 8 | 4 | 6 | 5 | 3 | 9 | 5 | 0.3212 | |
| 2 | 2 | 7 | 6 | 4 | 9 | 5 | 3 | 8 | 1 | 7 | 0.2000 | |
| 3 | 3 | 8 | 5 | 9 | 1 | 7 | 2 | 6 | 4 | 4 | 0.0788 | |
| 4 | 4 | 9 | 6 | 3 | 8 | 1 | 2 | 5 | 7 | 8 | -0.3939 | |
| 5 | 9 | 2 | 7 | 6 | 1 | 8 | 3 | 4 | 5 | 9 | -0.4545 | |
| 6 | 8 | 3 | 4 | 2 | 5 | 6 | 7 | 9 | 1 | 6 | 0.1152 | |
| 7 | 5 | 6 | 1 | 3 | 4 | 7 | 9 | 8 | 2 | 6 | 0.2727 | |
| 8 | 7 | 9 | 8 | 5 | 2 | 4 | 1 | 6 | 3 | 7 | -0.6242 | |
| 9 | 4 | 1 | 3 | 8 | 2 | 9 | 5 | 7 | 6 | 7 | 0.5636 | |
| 10 | 6 | 5 | 1 | 7 | 3 | 9 | 4 | 2 | 8 | 5 | -0.0788 | |
| u | 8 | 6 | 8 | 8 | 6 | 6 | 8 | 4 | 8 | 6 | 1 | |
| 6 | 0.3818 | -0.0667 | -0.0061 | -0.5273 | -0.0667 | 0.0303 | 0.4303 | 0.0303 | 0.1636 | 0.3697 | ||
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | u | rs |
| 1 | 3 | 9 | 6 | 2 | 4 | 8 | 7 | 1 | 5 | 5 | -0.2848 | |
| 2 | 6 | 9 | 2 | 7 | 3 | 1 | 5 | 8 | 4 | 7 | -0.1273 | |
| 3 | 4 | 5 | 1 | 3 | 9 | 6 | 2 | 7 | 8 | 5 | 0.4424 | |
| 4 | 1 | 3 | 5 | 9 | 6 | 8 | 7 | 4 | 2 | 4 | 0.3939 | |
| 5 | 9 | 2 | 6 | 4 | 8 | 7 | 5 | 3 | 1 | 5 | -0.2606 | |
| 6 | 5 | 8 | 4 | 2 | 7 | 3 | 6 | 1 | 9 | 7 | 0.2606 | |
| 7 | 8 | 1 | 7 | 5 | 2 | 4 | 9 | 6 | 3 | 8 | -0.1273 | |
| 8 | 7 | 6 | 1 | 4 | 5 | 3 | 8 | 9 | 2 | 8 | -0.1636 | |
| 9 | 2 | 4 | 3 | 8 | 1 | 9 | 6 | 5 | 7 | 6 | 0.3697 | |
| 10 | 7 | 8 | 5 | 1 | 9 | 2 | 3 | 4 | 6 | 7 | -0.5030 | |
| u | 6 | 6 | 8 | 6 | 6 | 4 | 7 | 5 | 8 | 6 | 2 | |
| rs | 0.4051 | 0.3450 | 0.2970 | -0.0667 | 0.0667 | -0.2727 | -0.2485 | 0.0424 | 0.2121 | -0.0788 | ||
| 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | u | rs |
| 1 | 9 | 1 | 5 | 6 | 7 | 8 | 4 | 2 | 3 | 7 | -0.4061 | |
| 2 | 2 | 9 | 8 | 4 | 1 | 5 | 3 | 7 | 6 | 5 | -0.1273 | |
| 3 | 1 | 8 | 2 | 7 | 9 | 4 | 6 | 3 | 5 | 5 | 0.2000 | |
| 4 | 8 | 6 | 5 | 2 | 7 | 3 | 1 | 9 | 4 | 5 | 0.0303 | |
| 5 | 5 | 7 | 4 | 1 | 2 | 6 | 3 | 8 | 9 | 8 | 0.5394 | |
| 6 | 3 | 2 | 1 | 9 | 8 | 4 | 6 | 5 | 7 | 5 | 0.3939 | |
| 7 | 6 | 5 | 7 | 3 | 8 | 2 | 1 | 4 | 9 | 6 | 0.0303 | |
| 8 | 3 | 9 | 4 | 1 | 5 | 7 | 2 | 6 | 8 | 5 | -0.1152 | |
| 9 | 7 | 4 | 6 | 8 | 3 | 9 | 5 | 1 | 2 | 6 | -0.3697 | |
| 10 | 4 | 3 | 6 | 5 | 9 | 2 | 7 | 8 | 1 | 8 | -0.1758 | |
| u | 8 | 6 | 6 | 6 | 4 | 7 | 7 | 8 | 7 | 7 | 3 | |
| rs | 0.1636 | 0.0788 | 0.2364 | -0.0545 | -0.2727 | 0.5152 | 0.0424 | -0.1516 | -0.1515 | -0.1152 | ||
| 4 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | u | rs |
| 1 | 3 | 2 | 8 | 5 | 4 | 1 | 7 | 9 | 6 | 6 | 0.3939 | |
| 2 | 8 | 2 | 6 | 9 | 1 | 3 | 4 | 7 | 5 | 4 | -0.3455 | |
| 3 | 8 | 5 | 7 | 4 | 2 | 9 | 6 | 3 | 1 | 7 | -0.0121 | |
| 4 | 1 | 4 | 5 | 3 | 2 | 7 | 6 | 8 | 9 | 9 | 0.5758 | |
| 5 | 7 | 4 | 8 | 6 | 5 | 9 | 1 | 2 | 3 | 5 | -0.6364 | |
| 6 | 2 | 6 | 3 | 9 | 1 | 8 | 5 | 4 | 7 | 6 | 0.3697 | |
| 7 | 6 | 9 | 1 | 3 | 7 | 4 | 2 | 5 | 8 | 5 | 0.2364 | |
| 8 | 9 | 7 | 6 | 1 | 3 | 8 | 2 | 5 | 4 | 8 | -0.3939 | |
| 9 | 5 | 1 | 7 | 8 | 6 | 4 | 9 | 3 | 2 | 6 | -0.1758 | |
| 10 | 4 | 3 | 9 | 2 | 5 | 7 | 8 | 6 | 1 | 6 | 0.0909 | |
| u | 6 | 4 | 6 | 4 | 8 | 8 | 4 | 10 | 4 | 6 | 4 | |
| rs | -0.0667 | -0.1152 | 0.2848 | -0.3333 | 0.2970 | -0.0783 | 0.4783 | 0.7272 | -0.1636 | -0.5758 | ||
附表 18(2) 20 个自然数的随机排列
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | u | rs | |
| 1 | 02 | 17 | 12 | 09 | 06 | 19 | 04 | 18 | 07 | 05 | 10 | 01 | 16 | 08 | 15 | 11 | 20 | 13 | 03 | 14 | 15 | 0.1293 |
| 2 | 19 | 04 | 03 | 15 | 13 | 10 | 17 | 12 | 09 | 16 | 05 | 02 | 06 | 11 | 08 | 20 | 07 | 18 | 01 | 14 | 16 | -0.0526 |
| 3 | 06 | 08 | 09 | 12 | 20 | 14 | 05 | 18 | 15 | 04 | 03 | 13 | 02 | 01 | 07 | 19 | 11 | 16 | 17 | 10 | 13 | 0.0992 |
| 4 | 10 | 17 | 15 | 12 | 01 | 03 | 18 | 19 | 09 | 06 | 02 | 04 | 04 | 14 | 20 | 16 | 07 | 05 | 08 | 13 | 12 | -0.0602 |
| 5 | 16 | 01 | 14 | 07 | 19 | 10 | 03 | 17 | 02 | 11 | 06 | 09 | 12 | 05 | 18 | 13 | 20 | 08 | 15 | 04 | 17 | 0.0752 |
| 6 | 13 | 20 | 11 | 10 | 04 | 01 | 17 | 18 | 14 | 05 | 16 | 02 | 19 | 03 | 07 | 12 | 08 | 06 | 09 | 15 | 11 | -0.1699 |
| 7 | 05 | 10 | 20 | 15 | 03 | 04 | 09 | 13 | 01 | 16 | 12 | 02 | 19 | 17 | 07 | 14 | 18 | 08 | 11 | 06 | 10 | 0.0962 |
| 8 | 17 | 14 | 09 | 15 | 05 | 13 | 02 | 08 | 18 | 04 | 16 | 03 | 06 | 11 | 01 | 19 | 20 | 10 | 07 | 12 | 10 | -0.0511 |
| 9 | 03 | 13 | 14 | 11 | 18 | 08 | 15 | 12 | 10 | 01 | 06 | 19 | 07 | 04 | 05 | 17 | 02 | 16 | 20 | 09 | 13 | 0.0286 |
| 10 | 07 | 16 | 02 | 11 | 09 | 17 | 15 | 05 | 14 | 03 | 12 | 13 | 06 | 20 | 01 | 04 | 08 | 18 | 10 | 19 | 11 | 0.1308 |
附表 18(3) 30 个自然数的随机排列
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | u | rs | |
| 1 | 20 | 12 | 05 | 03 | 26 | 21 | 17 | 09 | 24 | 19 | 14 | 06 | 22 | 11 | 28 | 29 | 27 | 30 | 08 | 02 | 15 | 18 | 01 | 25 | 16 | 04 | 07 | 13 | 10 | 23 | 18 | -0.0763 |
| 2 | 04 | 28 | 01 | 10 | 17 | 26 | 11 | 22 | 27 | 16 | 13 | 20 | 12 | 23 | 18 | 24 | 09 | 02 | 29 | 19 | 25 | 15 | 06 | 30 | 07 | 14 | 05 | 21 | 03 | 08 | 21 | -0.1204 |
| 3 | 18 | 21 | 24 | 04 | 20 | 02 | 23 | 17 | 16 | 13 | 27 | 11 | 05 | 12 | 06 | 28 | 01 | 14 | 09 | 22 | 10 | 08 | 29 | 07 | 30 | 15 | 03 | 25 | 19 | 26 | 15 | 0.0785 |
| 4 | 08 | 21 | 12 | 10 | 19 | 06 | 28 | 17 | 26 | 29 | 03 | 14 | 13 | 04 | 30 | 07 | 23 | 24 | 11 | 01 | 16 | 20 | 25 | 02 | 05 | 22 | 15 | 27 | 18 | 09 | 22 | -0.0024 |
| 5 | 27 | 14 | 16 | 23 | 30 | 25 | 01 | 04 | 11 | 24 | 12 | 22 | 03 | 21 | 05 | 20 | 18 | 13 | 15 | 07 | 10 | 02 | 28 | 08 | 09 | 26 | 19 | 06 | 29 | 17 | 17 | -0.0990 |
| 6 | 29 | 18 | 12 | 13 | 06 | 09 | 26 | 01 | 23 | 16 | 28 | 11 | 08 | 27 | 10 | 03 | 22 | 17 | 25 | 30 | 20 | 04 | 15 | 14 | 02 | 19 | 05 | 21 | 24 | 07 | 21 | -0.0785 |
| 7 | 28 | 14 | 20 | 11 | 30 | 10 | 05 | 09 | 25 | 04 | 19 | 16 | 29 | 07 | 18 | 12 | 08 | 15 | 17 | 02 | 27 | 23 | 03 | 26 | 01 | 22 | 24 | 13 | 21 | 06 | 17 | -0.0865 |
| 8 | 14 | 08 | 20 | 27 | 06 | 21 | 16 | 03 | 01 | 28 | 19 | 25 | 04 | 15 | 12 | 18 | 23 | 17 | 22 | 02 | 30 | 26 | 05 | 11 | 24 | 09 | 13 | 10 | 07 | 29 | 18 | 0.0376 |
| 9 | 10 | 14 | 09 | 29 | 05 | 24 | 18 | 07 | 26 | 23 | 04 | 01 | 28 | 19 | 11 | 13 | 02 | 25 | 03 | 30 | 16 | 06 | 21 | 12 | 17 | 22 | 20 | 08 | 15 | 27 | 18 | 0.1039 |
| 10 | 06 | 29 | 22 | 30 | 09 | 20 | 27 | 04 | 07 | 24 | 01 | 03 | 14 | 10 | 16 | 15 | 13 | 18 | 26 | 25 | 28 | 02 | 23 | 19 | 17 | 08 | 12 | 05 | 21 | 11 | 18 | -0.1012 |
附表 18(4) 40 个自然数的随机排列
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| 37 | 14 | 04 | 29 | 34 | 17 | 22 | 09 | 38 | 21 | 32 | 35 | 21 | 04 | 09 | 36 | 27 | 10 | 19 | 22 | 30 | 11 | 38 | 35 | 24 | 29 | 18 | 02 | 06 | 31 | |||
| 10 | 15 | 10 | 31 | 30 | 02 | 12 | 01 | 16 | 33 | 36 | 10 | 23 | 15 | 28 | 17 | 37 | 16 | 11 | 26 | 06 | 39 | 10 | 01 | 23 | 28 | 39 | 20 | 15 | 34 | 21 | 10 | 33 |
| 20 | 32 | 03 | 08 | 11 | 06 | 02 | 13 | 25 | 18 | 40 | 20 | 18 | 34 | 31 | 03 | 08 | 33 | 40 | 07 | 14 | 29 | 20 | 04 | 09 | 12 | 37 | 26 | 25 | 16 | 05 | 14 | 40 |
| 30 | 24 | 35 | 19 | 26 | 27 | 23 | 05 | 28 | 07 | 39 | 30 | 20 | 04 | 01 | 38 | 13 | 35 | 02 | 12 | 05 | 30 | 30 | 27 | 36 | 17 | 32 | 19 | 03 | 22 | 13 | 08 | 07 |
| u=27 r=0.0514 | u=31 r=0.0861 | u=34 r=-0.1737 | ||||||||||||||||||||||||||||||
| 2 | 4 | 6 | ||||||||||||||||||||||||||||||
| 19 | 26 | 31 | 38 | 23 | 06 | 15 | 40 | 27 | 33 | 21 | 30 | 02 | 27 | 03 | 16 | 20 | 04 | 25 | 15 | 23 | 34 | 27 | 18 | 26 | 17 | 36 | 24 | 05 | 22 | |||
| 10 | 02 | 03 | 16 | 10 | 37 | 18 | 11 | 21 | 04 | 36 | 10 | 12 | 39 | 11 | 24 | 35 | 29 | 36 | 28 | 19 | 34 | 10 | 03 | 16 | 32 | 01 | 31 | 20 | 07 | 12 | 37 | 28 |
| 20 | 25 | 08 | 05 | 22 | 17 | 39 | 12 | 24 | 07 | 29 | 20 | 33 | 18 | 10 | 23 | 37 | 06 | 17 | 08 | 13 | 40 | 20 | 30 | 25 | 13 | 11 | 14 | 04 | 06 | 35 | 40 | 29 |
| 30 | 28 | 13 | 34 | 20 | 09 | 32 | 14 | 01 | 30 | 35 | 30 | 01 | 26 | 09 | 38 | 05 | 22 | 31 | 14 | 32 | 07 | 30 | 33 | 08 | 10 | 39 | 02 | 19 | 09 | 38 | 15 | 21 |
| u=31 r=0.0383 | u=29 r=0.0199 | u=27 r=-0.0614 | ||||||||||||||||||||||||||||||
附表 18(5) 50 个自然数的随机排列
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| 38 | 09 | 42 | 08 | 47 | 21 | 50 | 07 | 39 | 30 | 16 | 35 | 25 | 38 | 23 | 42 | 28 | 45 | 18 | 37 | 43 | 12 | 41 | 07 | 50 | 13 | 49 | 14 | 05 | 26 | |||
| 10 | 36 | 12 | 23 | 32 | 40 | 27 | 24 | 33 | 10 | 11 | 10 | 34 | 41 | 01 | 12 | 39 | 04 | 27 | 44 | 03 | 32 | 10 | 15 | 22 | 37 | 20 | 44 | 25 | 31 | 40 | 29 | 36 |
| 30 | 28 | 49 | 45 | 29 | 46 | 15 | 17 | 44 | 03 | 22 | 30 | 49 | 15 | 46 | 09 | 22 | 47 | 06 | 31 | 10 | 43 | 30 | 47 | 03 | 16 | 28 | 39 | 19 | 02 | 34 | 45 | 10 |
| 30 | 01 | 06 | 20 | 18 | 25 | 16 | 35 | 48 | 05 | 41 | 30 | 14 | 08 | 19 | 11 | 36 | 07 | 20 | 21 | 02 | 17 | 30 | 42 | 23 | 04 | 11 | 32 | 06 | 17 | 46 | 27 | 09 |
| 40 | 14 | 31 | 19 | 02 | 26 | 13 | 34 | 43 | 04 | 37 | 40 | 26 | 48 | 29 | 05 | 24 | 40 | 13 | 30 | 33 | 50 | 40 | 24 | 48 | 33 | 13 | 30 | 01 | 38 | 21 | 35 | 08 |
| u=36r=-0.1553 | u=41r=-0.0972 | u=36r=-0.1219 | ||||||||||||||||||||||||||||||
| 2 | 4 | 6 | ||||||||||||||||||||||||||||||
| 02 | 30 | 41 | 40 | 04 | 37 | 49 | 22 | 07 | 10 | 10 | 07 | 24 | 37 | 22 | 46 | 25 | 32 | 17 | 13 | 48 | 01 | 31 | 38 | 17 | 20 | 03 | 30 | 37 | 18 | |||
| 10 | 31 | 24 | 47 | 50 | 45 | 14 | 25 | 44 | 03 | 39 | 10 | 04 | 11 | 45 | 29 | 26 | 05 | 02 | 47 | 40 | 09 | 10 | 29 | 05 | 50 | 11 | 44 | 25 | 06 | 23 | 42 | 28 |
| 20 | 12 | 01 | 43 | 28 | 49 | 17 | 20 | 05 | 36 | 13 | 20 | 16 | 41 | 36 | 19 | 27 | 48 | 33 | 14 | 39 | 08 | 30 | 04 | 49 | 36 | 26 | 15 | 14 | 43 | 22 | 39 | 13 |
| 30 | 06 | 21 | 27 | 08 | 33 | 42 | 09 | 29 | 36 | 18 | 30 | 42 | 15 | 38 | 23 | 30 | 50 | 34 | 06 | 49 | 28 | 30 | 10 | 19 | 41 | 32 | 07 | 24 | 47 | 08 | 46 | 21 |
| 40 | 15 | 48 | 11 | 16 | 26 | 35 | 32 | 23 | 19 | 34 | 40 | 43 | 12 | 21 | 01 | 18 | 20 | 35 | 03 | 44 | 34 | 40 | 35 | 40 | 27 | 02 | 33 | 34 | 09 | 12 | 45 | 16 |
| u=39 r=-0.0555 | u=39 r=-0.1000 | U=41 r=0.0088 | ||||||||||||||||||||||||||||||
附表 18(6) 100 个自然数的随机排列
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||
| 26 | 03 | 86 | 73 | 36 | 91 | 84 | 11 | 19 | 76 | 48 | 73 | 12 | 37 | 19 | 62 | 47 | 10 | 16 | 51 | 44 | 12 | 07 | 86 | 09 | 48 | 53 | 63 | 66 | 89 | |||
| 10 | 23 | 08 | 20 | 85 | 64 | 35 | 57 | 80 | 43 | 72 | 10 | 96 | 31 | 57 | 36 | 54 | 81 | 30 | 55 | 86 | 93 | 10 | 31 | 64 | 61 | 19 | 94 | 73 | 92 | 59 | 00 | 70 |
| 20 | 49 | 34 | 97 | 60 | 88 | 69 | 96 | 41 | 74 | 01 | 20 | 88 | 09 | 03 | 66 | 65 | 78 | 84 | 61 | 53 | 34 | 20 | 72 | 03 | 89 | 34 | 96 | 15 | 95 | 28 | 85 | 20 |
| 30 | 51 | 52 | 47 | 66 | 93 | 81 | 48 | 31 | 02 | 44 | 30 | 44 | 25 | 98 | 83 | 28 | 59 | 92 | 13 | 56 | 79 | 30 | 80 | 75 | 82 | 69 | 60 | 98 | 85 | 02 | 67 | 45 |
| 40 | 04 | 53 | 98 | 25 | 21 | 06 | 28 | 62 | 85 | 17 | 40 | 14 | 45 | 76 | 43 | 63 | 18 | 94 | 85 | 80 | 41 | 40 | 52 | 79 | 04 | 13 | 77 | 06 | 11 | 91 | 76 | 08 |
| 50 | 00 | 27 | 40 | 13 | 22 | 50 | 09 | 71 | 24 | 39 | 50 | 70 | 91 | 46 | 29 | 05 | 17 | 26 | 33 | 06 | 42 | 50 | 43 | 36 | 27 | 54 | 01 | 40 | 29 | 42 | 17 | 38 |
| 60 | 58 | 83 | 78 | 94 | 33 | 18 | 45 | 79 | 12 | 95 | 60 | 27 | 75 | 40 | 23 | 04 | 52 | 71 | 88 | 74 | 11 | 60 | 07 | 24 | 97 | 26 | 47 | 18 | 58 | 41 | 90 | 05 |
| 70 | 15 | 90 | 57 | 16 | 52 | 75 | 05 | 30 | 79 | 36 | 70 | 60 | 72 | 01 | 95 | 20 | 68 | 99 | 69 | 67 | 24 | 70 | 92 | 49 | 74 | 99 | 50 | 88 | 25 | 71 | 14 | 81 |
| 80 | 70 | 63 | 67 | 68 | 61 | 46 | 10 | 87 | 42 | 65 | 80 | 07 | 58 | 35 | 32 | 89 | 15 | 02 | 87 | 90 | 62 | 80 | 65 | 57 | 10 | 30 | 55 | 21 | 78 | 56 | 51 | 62 |
| 90 | 61 | 88 | 59 | 29 | 82 | 07 | 14 | 92 | 99 | 89 | 90 | 21 | 50 | 49 | 64 | 00 | 79 | 08 | 97 | 22 | 39 | 90 | 39 | 93 | 68 | 22 | 23 | 16 | 83 | 33 | 46 | 84 |
| u=74 r=0.065910 | u=76 r=-0.0459 | u=79 r=-0.034 | ||||||||||||||||||||||||||||||
附表 19(1) 两样本率比较时所需样本含量(单侧)
上行:α=0.05,1-β=0.80
中行:α=0.05,1-β=0.90
下行:α=0.01,1-β=0.95
| 较小率 (%) | δ= 两组率之差(%) | |||||||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | |
| 5 | 330 | 105 | 55 | 35 | 25 | 20 | 16 | 13 | 11 | 9 | 8 | 7 | 6 | 6 |
| 460 | 145 | 76 | 48 | 34 | 26 | 21 | 17 | 15 | 13 | 11 | 9 | 8 | 7 | |
| 850 | 270 | 140 | 89 | 63 | 47 | 37 | 30 | 25 | 21 | 19 | 17 | 14 | 13 | |
| 10 | 540 | 155 | 76 | 47 | 32 | 23 | 19 | 15 | 13 | 11 | 9 | 8 | 7 | 6 |
| 740 | 210 | 105 | 64 | 44 | 33 | 25 | 21 | 17 | 14 | 12 | 11 | 9 | 8 | |
| 1370 | 390 | 195 | 120 | 81 | 60 | 46 | 37 | 30 | 25 | 21 | 19 | 16 | 14 | |
| 15 | 710 | 200 | 94 | 56 | 38 | 27 | 21 | 17 | 14 | 12 | 10 | 8 | 7 | 6 |
| 990 | 270 | 130 | 77 | 52 | 38 | 29 | 22 | 19 | 16 | 13 | 10 | 10 | 8 | |
| 1820 | 500 | 240 | 145 | 96 | 69 | 52 | 41 | 33 | 27 | 22 | 20 | 17 | 14 | |
| 20 | 860 | 230 | 110 | 63 | 42 | 30 | 22 | 18 | 15 | 12 | 10 | 8 | 7 | 6 |
| 1190 | 320 | 150 | 88 | 58 | 41 | 31 | 24 | 20 | 16 | 14 | 11 | 10 | 8 | |
| 2190 | 590 | 280 | 160 | 105 | 76 | 57 | 44 | 35 | 28 | 23 | 20 | 17 | 14 | |
| 25 | 980 | 260 | 120 | 69 | 45 | 32 | 24 | 19 | 15 | 12 | 10 | 8 | 7 | — |
| 1360 | 360 | 165 | 96 | 63 | 44 | 33 | 25 | 21 | 16 | 14 | 11 | 9 | — | |
| 2510 | 660 | 300 | 175 | 115 | 81 | 60 | 46 | 36 | 29 | 23 | 20 | 16 | — | |
| 30 | 1080 | 280 | 130 | 73 | 47 | 33 | 24 | 19 | 15 | 12 | 10 | 8 | — | — |
| 1500 | 390 | 175 | 100 | 65 | 46 | 33 | 25 | 21 | 16 | 13 | 11 | — | — | |
| 2760 | 720 | 330 | 185 | 120 | 84 | 61 | 47 | 36 | 28 | 22 | 19 | — | — | |
| 35 | 1160 | 300 | 135 | 75 | 48 | 33 | 24 | 19 | 15 | 12 | 9 | — | — | — |
| 1600 | 410 | 185 | 105 | 67 | 46 | 33 | 25 | 20 | 16 | 12 | — | — | — | |
| 2960 | 750 | 340 | 190 | 125 | 85 | 61 | 46 | 35 | 27 | 21 | — | — | — | |
| 40 | 1210 | 310 | 135 | 76 | 48 | 33 | 24 | 18 | 14 | 11 | — | — | — | — |
| 1670 | 420 | 190 | 105 | 67 | 46 | 33 | 24 | 19 | 14 | — | — | — | — | |
| 3080 | 780 | 350 | 195 | 125 | 84 | 60 | 44 | 33 | 25 | — | — | — | — | |
| 45 | 1230 | 310 | 135 | 75 | 47 | 32 | 22 | 17 | 13 | — | — | — | — | — |
| 1710 | 430 | 190 | 105 | 65 | 44 | 31 | 22 | 17 | — | — | — | — | — | |
| 3140 | 790 | 350 | 190 | 120 | 81 | 57 | 41 | 30 | — | — | — | — | — | |
| 50 | 1230 | 310 | 135 | 73 | 45 | 30 | 21 | 15 | — | — | — | — | — | — |
| 1710 | 420 | 185 | 100 | 63 | 41 | 29 | 21 | — | — | — | — | — | — | |
| 3140 | 780 | 340 | 185 | 115 | 76 | 52 | 37 | — | — | — | — | — | — | |
附表 19(2)两样本率比较时所需样本含量(双侧)
上行:α=0.05,1-β=0.80
中行:α=0.05,1-β=0.90
下行:α=0.01,1-β=0.95
| 较小率 (%) | δ= 两组率之差(%) | |||||||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | |
| 5 | 420 | 130 | 69 | 44 | 31 | 24 | 20 | 16 | 14 | 12 | 10 | 9 | 9 | 7 |
| 570 | 175 | 93 | 59 | 42 | 32 | 25 | 21 | 18 | 15 | 13 | 11 | 10 | 9 | |
| 960 | 300 | 155 | 10 | 71 | 54 | 42 | 34 | 28 | 24 | 21 | 19 | 16 | 14 | |
| 10 | 680 | 195 | 96 | 59 | 41 | 30 | 23 | 19 | 16 | 13 | 11 | 10 | 9 | 7 |
| 910 | 260 | 130 | 79 | 54 | 40 | 31 | 24 | 21 | 18 | 15 | 13 | 11 | 10 | |
| 1550 | 440 | 220 | 135 | 92 | 68 | 52 | 41 | 34 | 28 | 23 | 21 | 18 | 15 | |
| 15 | 910 | 250 | 120 | 71 | 48 | 34 | 26 | 21 | 17 | 14 | 12 | 10 | 9 | 8 |
| 1220 | 330 | 160 | 95 | 64 | 46 | 35 | 27 | 22 | 19 | 16 | 13 | 11 | 10 | |
| 2060 | 560 | 270 | 160 | 110 | 78 | 59 | 47 | 37 | 31 | 25 | 21 | 19 | 16 | |
| 20 | 1090 | 290 | 135 | 80 | 53 | 38 | 28 | 22 | 18 | 15 | 13 | 10 | 9 | 7 |
| 1460 | 390 | 185 | 105 | 71 | 51 | 38 | 29 | 23 | 20 | 16 | 14 | 11 | 10 | |
| 2470 | 660 | 310 | 180 | 120 | 86 | 64 | 50 | 40 | 32 | 26 | 21 | 19 | 15 | |
| 25 | 1250 | 330 | 150 | 88 | 57 | 40 | 30 | 23 | 19 | 15 | 13 | 10 | 9 | — |
| 1680 | 440 | 200 | 115 | 77 | 54 | 40 | 31 | 24 | 20 | 16 | 13 | 11 | — | |
| 2840 | 740 | 340 | 200 | 130 | 92 | 68 | 52 | 41 | 32 | 26 | 21 | 18 | — | |
| 30 | 1380 | 360 | 160 | 93 | 60 | 42 | 31 | 23 | 19 | 15 | 12 | 10 | — | — |
| 1840 | 480 | 220 | 125 | 80 | 56 | 41 | 31 | 24 | 20 | 16 | 13 | — | — | |
| 3120 | 810 | 370 | 210 | 135 | 95 | 69 | 53 | 41 | 32 | 25 | 21 | — | — | |
| 35 | 1470 | 380 | 170 | 96 | 61 | 42 | 31 | 23 | 18 | 14 | 11 | — | — | — |
| 1970 | 500 | 225 | 130 | 82 | 57 | 41 | 31 | 23 | 19 | 15 | — | — | — | |
| 3340 | 850 | 380 | 215 | 140 | 96 | 69 | 52 | 40 | 31 | 23 | — | — | — | |
| 40 | 1530 | 390 | 175 | 97 | 61 | 42 | 30 | 22 | 17 | 13 | — | — | — | — |
| 2050 | 520 | 230 | 130 | 82 | 56 | 40 | 29 | 22 | 18 | — | — | — | — | |
| 3480 | 880 | 390 | 220 | 140 | 95 | 68 | 50 | 37 | 28 | — | — | — | — | |
| 45 | 1560 | 390 | 175 | 96 | 60 | 40 | 28 | 21 | 16 | — | — | — | — | — |
| 2100 | 520 | 230 | 130 | 80 | 54 | 38 | 27 | 21 | — | — | — | — | — | |
| 3550 | 890 | 390 | 215 | 135 | 92 | 64 | 47 | 34 | — | — | — | — | — | |
| 50 | 1560 | 390 | 170 | 93 | 57 | 38 | 26 | 19 | — | — | — | — | — | — |
| 2100 | 520 | 225 | 125 | 77 | 51 | 35 | 24 | — | — | — | — | — | — | |
| 3550 | 880 | 380 | 210 | 130 | 86 | 59 | 41 | — | — | — | — | — | — | |
附表 20 配对比较(t 检验)时所需样本含量
| 单侧:α=0.005 双侧:α=0.01 | 单侧:α=0.01 双侧:α=0.02 | 单侧:α=0.025 双侧:α=0.05 | 单侧:α=0.05 双侧:α=0.1 | δ | ||||||||||||||||||
| 1-β=0.99 | 0.95 | 0.9 | 0.8 | 0.5 | 0.99 | 0.95 | 0.9 | 0.3 | 0.5 | 0.99 | 0.95 | 0.9 | 0.8 | 0.5 | 0.99 | 0.95 | 0.9 | 0.8 | 0.5 | |||
| 0.05 | 0.05 | |||||||||||||||||||||
| 0.10 | 0.10 | |||||||||||||||||||||
| 0.15 | 122 | 0.15 | ||||||||||||||||||||
| 0.20 | 139 | 99 | 70 | 0.20 | ||||||||||||||||||
| 0.25 | 110 | 90 | 128 | 64 | 139 | 101 | 45 | 0.25 | ||||||||||||||
| 0.30 | 134 | 78 | 115 | 63 | 119 | 90 | 45 | 122 | 97 | 71 | 32 | 0.30 | ||||||||||
| 0.35 | 125 | 99 | 58 | 109 | 85 | 47 | 109 | 88 | 67 | 34 | 90 | 72 | 52 | 24 | 0.35 | |||||||
| 0.40 | 115 | 97 | 77 | 45 | 101 | 85 | 66 | 37 | 117 | 84 | 68 | 51 | 26 | 101 | 70 | 55 | 40 | 19 | 0.40 | |||
| 0.45 | 92 | 77 | 62 | 37 | 110 | 81 | 68 | 53 | 30 | 93 | 67 | 54 | 41 | 21 | 80 | 55 | 44 | 33 | 15 | 0.45 | ||
| 0.50 | 100 | 75 | 63 | 51 | 30 | 90 | 66 | 55 | 43 | 25 | 76 | 54 | 44 | 34 | 18 | 65 | 45 | 36 | 27 | 13 | 0.50 | |
| 0.55 | 83 | 63 | 53 | 42 | 26 | 75 | 55 | 46 | 36 | 21 | 63 | 45 | 37 | 28 | 15 | 54 | 38 | 30 | 22 | 11 | 0.55 | |
| 0.60 | 71 | 53 | 45 | 36 | 22 | 63 | 47 | 39 | 31 | 18 | 53 | 38 | 32 | 24 | 13 | 46 | 32 | 26 | 19 | 9 | 0.60 | |
| 0.65 | 61 | 46 | 39 | 31 | 20 | 55 | 41 | 34 | 27 | 16 | 46 | 33 | 27 | 21 | 12 | 39 | 28 | 22 | 17 | 8 | 0.65 | |
| 0.70 | 53 | 40 | 34 | 28 | 17 | 47 | 35 | 30 | 24 | 14 | 40 | 29 | 24 | 19 | 10 | 34 | 24 | 19 | 15 | 8 | 0.70 | |
| 0.75 | 47 | 36 | 30 | 25 | 16 | 42 | 31 | 27 | 21 | 13 | 35 | 26 | 21 | 16 | 9 | 30 | 21 | 17 | 13 | 7 | 0.75 | |
| 0.80 | 41 | 32 | 27 | 22 | 14 | 37 | 23 | 24 | 19 | 12 | 31 | 22 | 19 | 15 | 9 | 27 | 19 | 15 | 12 | 6 | 0.80 | |
| 0.85 | 37 | 29 | 24 | 20 | 13 | 33 | 25 | 24 | 17 | 11 | 28 | 21 | 17 | 13 | 8 | 24 | 17 | 14 | 11 | 6 | 0.85 | |
| 0.90 | 34 | 26 | 22 | 18 | 12 | 29 | 23 | 19 | 16 | 10 | 25 | 19 | 16 | 12 | 7 | 21 | 15 | 13 | 10 | 5 | 0.90 | |
| 0.95 | 31 | 24 | 20 | 17 | 11 | 27 | 21 | 18 | 14 | 9 | 23 | 17 | 14 | 11 | 7 | 19 | 14 | 11 | 9 | 5 | 0.95 | |
| 1.00 | 28 | 22 | 19 | 16 | 10 | 25 | 19 | 16 | 13 | 9 | 21 | 16 | 13 | 10 | 6 | 18 | 13 | 11 | 8 | 5 | 1.00 | |
| 1.1 | 24 | 19 | 16 | 14 | 9 | 21 | 16 | 14 | 12 | 8 | 18 | 13 | 11 | 9 | 6 | 15 | 11 | 9 | 7 | 1.1 | ||
| 1.2 | 21 | 16 | 14 | 12 | 8 | 18 | 14 | 12 | 10 | 7 | 15 | 12 | 10 | 8 | 5 | 13 | 10 | 8 | 6 | 1.2 | ||
| 1.3 | 18 | 15 | 13 | 11 | 8 | 16 | 13 | 11 | 9 | 6 | 14 | 10 | 9 | 7 | 11 | 8 | 7 | 6 | 1.3 | |||
| 1.4 | 16 | 13 | 12 | 10 | 7 | 14 | 11 | 10 | 9 | 6 | 12 | 9 | 8 | 7 | 10 | 8 | 7 | 5 | 1.4 | |||
| 1.5 | 15 | 12 | 11 | 9 | 7 | 13 | 10 | 9 | 8 | 6 | 11 | 8 | 7 | 6 | 9 | 7 | 6 | 1.5 | ||||
| 1.6 | 13 | 11 | 10 | 8 | 6 | 12 | 10 | 9 | 7 | 5 | 10 | 8 | 7 | 6 | 8 | 6 | 6 | 1.6 | ||||
| 1.7 | 12 | 10 | 9 | 8 | 6 | 10 | 9 | 8 | 7 | 9 | 7 | 6 | 5 | 8 | 6 | 5 | 1.7 | |||||
| 1.8 | 12 | 10 | 9 | 8 | 6 | 10 | 8 | 7 | 7 | 8 | 7 | 6 | 7 | 6 | 1.8 | |||||||
| 1.9 | 11 | 9 | 8 | 7 | 6 | 10 | 8 | 7 | 6 | 8 | 6 | 6 | 7 | 5 | 1.9 | |||||||
| 2.0 | 10 | 8 | 8 | 7 | 5 | 9 | 7 | 7 | 6 | 7 | 6 | 5 | 6 | 2.0 | ||||||||
| 2.1 | 10 | 8 | 7 | 7 | 8 | 7 | 6 | 6 | 7 | 6 | 6 | 2.1 | ||||||||||
| 2.2 | 9 | 8 | 7 | 6 | 8 | 7 | 6 | 5 | 7 | 6 | 6 | 2.2 | ||||||||||
| 2.3 | 9 | 7 | 7 | 6 | 8 | 6 | 6 | 6 | 5 | 5 | 2.3 | |||||||||||
| 2.4 | 8 | 7 | 7 | 6 | 7 | 6 | 6 | 6 | 2.4 | |||||||||||||
| 2.5 | 8 | 7 | 6 | 6 | 7 | 6 | 6 | 6 | 2.5 | |||||||||||||
| 3.0 | 7 | 6 | 6 | 5 | 6 | 5 | 5 | 5 | 3.0 | |||||||||||||
| 3.5 | 6 | 5 | 5 | 5 | 3.5 | |||||||||||||||||
| 4.0 | 6 | 4.0 | ||||||||||||||||||||
附表 21 两样本均数(t 检验)时所需样本含量
| δ | 单侧:α=0.005 双侧:α=0.01 | 单侧:α=0.005 双侧:α=0.01 | 单侧:α=0.005 双侧:α=0.01 | 单侧:α=0.005 双侧:α=0.01 | δ | ||||||||||||||||
| 1-β=0.99 | 0.95 | 0.9 | 0.8 | 0.5 | 0.99 | 0.95 | 0.9 | 0.8 | 0.5 | 0. 9 | 0.95 | 0.9 | 0.8 | 0.5 | 0.99 | 0.95 | 0.9 | 0.8 | 0.5 | ||
| 0.05 | 0.05 | ||||||||||||||||||||
| 0.10 | 0.10 | ||||||||||||||||||||
| 0.15 | 0.15 | ||||||||||||||||||||
| 0.20 | 137 | 0.20 | |||||||||||||||||||
| 0.25 | 124 | 88 | 0.25 | ||||||||||||||||||
| 0.30 | 123 | 87 | 61 | 0.30 | |||||||||||||||||
| 0.35 | 110 | 90 | 64 | 102 | 45 | 0.35 | |||||||||||||||
| 0.40 | 85 | 70 | 100 | 50 | 108 | 78 | 35 | 0.40 | |||||||||||||
| 0.45 | 118 | 68 | 101 | 55 | 105 | 79 | 39 | 108 | 86 | 62 | 28 | 0.45 | |||||||||
| 0.50 | 96 | 55 | 106 | 82 | 45 | 106 | 86 | 64 | 32 | 88 | 70 | 51 | 23 | 0.50 | |||||||
| 0.55 | 101 | 79 | 46 | 106 | 88 | 68 | 38 | 87 | 71 | 53 | 27 | 112 | 73 | 58 | 42 | 19 | 0.55 | ||||
| 0.60 | 101 | 85 | 67 | 39 | 90 | 74 | 58 | 32 | 104 | 74 | 60 | 45 | 23 | 89 | 61 | 49 | 36 | 16 | 0.60 | ||
| 0.65 | 87 | 73 | 57 | 34 | 104 | 77 | 64 | 49 | 27 | 88 | 63 | 51 | 39 | 20 | 76 | 52 | 42 | 30 | 14 | 0.65 | |
| 0.70 | 100 | 75 | 63 | 50 | 29 | 90 | 66 | 55 | 43 | 24 | 76 | 55 | 44 | 34 | 17 | 66 | 45 | 36 | 26 | 12 | 0.70 |
| 0.75 | 88 | 66 | 55 | 44 | 26 | 79 | 58 | 48 | 38 | 21 | 67 | 48 | 39 | 29 | 15 | 57 | 40 | 32 | 23 | 11 | 0.75 |
| 0.80 | 77 | 58 | 49 | 39 | 23 | 70 | 51 | 43 | 33 | 19 | 59 | 42 | 34 | 26 | 14 | 50 | 35 | 28 | 21 | 10 | 0.80 |
| 0.85 | 69 | 51 | 43 | 35 | 21 | 62 | 46 | 38 | 30 | 17 | 52 | 37 | 31 | 23 | 12 | 45 | 31 | 25 | 18 | 9 | 0.85 |
| 0.90 | 62 | 46 | 39 | 31 | 19 | 55 | 41 | 34 | 27 | 15 | 47 | 34 | 27 | 21 | 11 | 40 | 28 | 22 | 16 | 8 | 0.90 |
| 0.95 | 55 | 42 | 35 | 28 | 17 | 50 | 37 | 31 | 24 | 14 | 42 | 30 | 25 | 19 | 10 | 36 | 25 | 20 | 15 | 7 | 0.95 |
| 1.00 | 50 | 38 | 32 | 26 | 15 | 45 | 33 | 28 | 22 | 13 | 38 | 27 | 23 | 17 | 9 | 33 | 23 | 18 | 14 | 7 | 1.00 |
| 1.1 | 42 | 32 | 27 | 22 | 13 | 38 | 28 | 23 | 19 | 11 | 32 | 23 | 19 | 14 | 8 | 27 | 19 | 15 | 12 | 6 | 1.1 |
| 1.2 | 36 | 27 | 23 | 18 | 11 | 32 | 24 | 20 | 16 | 9 | 27 | 20 | 16 | 12 | 7 | 23 | 16 | 13 | 10 | 5 | 1.2 |
| 1.3 | 31 | 23 | 20 | 16 | 10 | 28 | 21 | 17 | 14 | 8 | 23 | 17 | 14 | 11 | 6 | 20 | 14 | 11 | 9 | 5 | 1.3 |
| 1.4 | 27 | 20 | 17 | 14 | 9 | 24 | 18 | 15 | 12 | 8 | 20 | 15 | 12 | 10 | 6 | 17 | 12 | 10 | 8 | 4 | 1.4 |
| 1.5 | 24 | 18 | 15 | 13 | 8 | 21 | 16 | 14 | 11 | 7 | 18 | 13 | 11 | 9 | 5 | 15 | 11 | 9 | 7 | 4 | 1.5 |
| 1.6 | 21 | 16 | 14 | 11 | 7 | 19 | 14 | 12 | 10 | 6 | 16 | 12 | 10 | 8 | 5 | 14 | 10 | 8 | 6 | 4 | 1.6 |
| 1.7 | 19 | 15 | 13 | 10 | 7 | 17 | 13 | 11 | 9 | 6 | 14 | 11 | 9 | 7 | 4 | 12 | 9 | 7 | 6 | 3 | 1.7 |
| 1.8 | 17 | 13 | 11 | 10 | 6 | 15 | 12 | 10 | 8 | 5 | 13 | 10 | 8 | 6 | 4 | 11 | 8 | 7 | 5 | 1.8 | |
| 1.9 | 16 | 12 | 11 | 9 | 6 | 14 | 11 | 9 | 8 | 5 | 12 | 9 | 7 | 6 | 4 | 10 | 7 | 6 | 5 | 1.9 | |
| 2.0 | 14 | 11 | 10 | 8 | 6 | 13 | 10 | 9 | 7 | 5 | 11 | 8 | 7 | 6 | 4 | 9 | 7 | 6 | 4 | 2.0 | |
| 2.1 | 13 | 10 | 9 | 8 | 5 | 12 | 9 | 8 | 7 | 5 | 10 | 8 | 6 | 5 | 3 | 8 | 6 | 5 | 4 | 2.1 | |
| 2.2 | 12 | 10 | 8 | 7 | 5 | 11 | 9 | 7 | 6 | 4 | 9 | 7 | 6 | 5 | 8 | 6 | 5 | 4 | 2.2 | ||
| 2.3 | 11 | 9 | 8 | 7 | 5 | 10 | 8 | 7 | 6 | 4 | 9 | 7 | 6 | 5 | 7 | 5 | 5 | 4 | 2.3 | ||
| 2.4 | 11 | 9 | 8 | 6 | 5 | 10 | 8 | 7 | 6 | 4 | 8 | 6 | 5 | 4 | 7 | 5 | 4 | 4 | 2.4 | ||
| 2.5 | 10 | 8 | 7 | 6 | 4 | 9 | 7 | 6 | 5 | 4 | 8 | 6 | 5 | 4 | 6 | 5 | 4 | 3 | 2.5 | ||
| 3.0 | 8 | 6 | 6 | 5 | 4 | 7 | 6 | 5 | 4 | 3 | 6 | 5 | 4 | 4 | 5 | 4 | 3 | 3.0 | |||
| 3.5 | 6 | 5 | 5 | 4 | 3 | 6 | 5 | 4 | 4 | 5 | 4 | 4 | 3 | 4 | 3 | 3.5 | |||||
| 4.0 | 6 | 6 | 4 | 4 | 5 | 4 | 4 | 3 | 4 | 4 | 3 | 4 | 4.0 | ||||||||
英汉统计名词对照
A
| abscissa | 横坐标 |
| absence rate | 缺勤率 |
| absolute number | 绝对数 |
| absolute value | 绝对值 |
| accident error | 偶然误差 |
| accumulated frequency | 累积频数 |
| alternative hypothesis | 备择假设 |
| analysis of data | 分析资料 |
| analysis of variance(ANOVA) | 方差分析 |
| arith-log paper | 算术对数纸 |
| arithmetic mean | 算术均数 |
| assumed mean | 假定均数 |
| arithmetic weighted mean | 加权算术均数 |
| asymmetry coefficient | 偏度系数 |
| average | 平均数 |
| average deviation | 平均差 |
B
| bar chart | 直条图、条图 |
| bias | 偏性 |
| binomial distribution | 二项分布 |
| biometrics | 生物统计学 |
| bivariate normal population | 双变量正态总体 |
C
| cartogram | 统计图 |
| case fatality rate(or case mortality) | 病死率 |
| census | 普查 |
| chi-sguare(X2) test | 卡方检验 |
| central tendency | 集中趋势 |
| class interval | 组距 |
| classification | 分组、分类 |
| cluster sampling | 整群抽样 |
| coefficient of correlation | 相关系数 |
| coefficient of regression | 回归系数 |
| coefficient of variability(or coefficieut of variation) | 变异系数 |
| collection of data | 收集资料 |
| column | 列(栏) |
| combinative table | 组合表 |
| combined standard deviation | 合并标准差 |
| combined variance(or poolled variance) | 合并方差 |
| complete survey | 全面调查 |
| completely correlation | 完全相关 |
| completely random design | 完全随机设计 |
| confidence interval | 可信区间,置信区间 |
| confidence level | 可信水平,置信水平 |
| confidence limit | 可信限,置信限 |
| constituent ratio | 构成比,结构相对数 |
| continuity | 连续性 |
| control | 对照 |
| control group | 对照组 |
| coordinate | 坐标 |
| correction for continuity | 连续性校正 |
| correction for grouping | 归组校正 |
| correction number | 校正数 |
| correction value | 校正值 |
| correlation | 相关,联系 |
| correlation analysis | 相关分析 |
| correlation coefficient | 相关系数 |
| critical value | 临界值 |
| cumulative frequency | 累积频率 |
D
| data | 资料 |
| degree of confidence | 可信度,置信度 |
| degree of dispersion | 离散程度 |
| degree of freedom | 自由度 |
| degree of variation | 变异度 |
| dependent variable | 应变量 |
| design of experiment | 实验设计 |
| deviation from the mean | 离均差 |
| diagnose accordance rate | 诊断符合率 |
| difference with significance | 差别不显著 |
| difference with significance | 差别显著 |
| discrete variable | 离散变量 |
| dispersion tendency | 离中趋势 |
| distribution | 分布、分配 |
E
| effective rate | 有效率 |
| eigenvalue | 特征值 |
| enumeration data | 计数资料 |
| equation of linear regression | 线性回归方程 |
| error | 误差 |
| error of replication | 重复误差 |
| error of type II | Ⅱ型错误,第二类误差 |
| error of type I | Ⅰ型错误,第一类误差 |
| estimate value | 估计值 |
| event | 事件 |
| experiment design | 实验设计 |
| experiment error | 实验误差 |
| experimental group | 实验组 |
| extreme value | 极值 |
F
| fatality rate | 病死率 |
| field survey | 现场调查 |
| fourfold table | 四格表 |
| freguency | 频数 |
| freguency distribution | 频数分布 |
G
| Gaussian curve | 高斯曲线 |
| geometric mean | 几何均数 |
| grouped data | 分组资料 |
H
| histogram | 直方图 |
| homogeneity of variance | 方差齐性 |
| homogeneity test of variances | 方差齐性检验 |
| hypothesis test | 假设检验 |
| hypothetical universe | 假设总体 |
I
| incidence rate | 发病率 |
| incomplete survey | 非全面调检 |
| indepindent variable | 自变量 |
| indivedual difference | 个体差异 |
| infection rate | 感染率 |
| inferior limit | 下限 |
| initial data | 原始数据 |
| inspection of data | 检查资料 |
| intercept | 截距 |
| interpolation method | 内插法 |
| interval estimation | 区间估计 |
| inverse correlation | 负相关 |
K
| kurtosis coefficient | 峰度系数 |
L
| latin sguare design | 拉丁方设计 |
| least significant difference | 最小显着差数 |
| least square method | 最小平方法,最小乘法 |
| leptokurtic distribution | 尖峭态分布 |
| leptokurtosis | 峰态,峭度 |
| linear chart | 线图 |
| linear correlation | 直线相关 |
| linear regression | 直线回归 |
| linear regression eguation | 直线回归方程 |
| link relative | 环比 |
| logarithmic normal distribution | 对数正态分布 |
| logarithmic scale | 对数尺度 |
| lognormal distribution | 对数正态分布 |
| lower limit | 下限 |
M
| matched pair design | 配对设计 |
| mathematical statistics | 数理统计(学) |
| maximum value | 极大值 |
| mean | 均值 |
| mean of population | 总体均数 |
| mean square | 均方 |
| mean variance | 均方,方差 |
| measurement data | 讲量资料 |
| median | 中位数 |
| medical statistics | 医学统计学 |
| mesokurtosis | 正态峰 |
| method of least squares | 最小平方法,最小乘法 |
| method of grouping | 分组法 |
| method of percentiles | 百分位数法 |
| mid-value of class | 组中值 |
| minimum value | 极小值 |
| mode | 众数 |
| moment | 动差,矩 |
| morbidity | 患病率 |
| mortality | 死亡率 |
N
| natality | 出生率 |
| natural logarithm | 自然对数 |
| negative correlation | 负相关 |
| negative skewness | 负偏志 |
| no correlation | 无相关 |
| non-linear correlation | 非线性相关 |
| non-parametric statistics | 非参数统计 |
| normal curve | 正态曲线 |
| normal deviate | 正态离差 |
| normal distribution | 正态分布 |
| normal population | 正态总体 |
| normal probability curve | 正态概率曲线 |
| normal range | 正常范围 |
| normal value | 正常值 |
| normal kurtosis | 正态峰 |
| normality test | 正态性检验 |
| nosometry | 患病率 |
| null hypothesis | 无效假设,检验假设 |
O
| observed unit | 观察单位 |
| observed value | 观察值 |
| one-sided test | 单测检验 |
| one-tailed test | 单尾检验 |
| order statistic | 顺序统计量 |
| ordinal number | 秩号 |
| ordinate | 纵坐标 |
P
| pairing data | 配对资料 |
| parameter | 参数 |
| percent | 百分率 |
| percentage | 百分数,百分率 |
| percentage bar chart | 百分条图 |
| percentile | 百分位数 |
| pie diagram | 园图 |
| placebo | 安慰剂 |
| planning of survey | 调查计划 |
| point estimation | 点估计 |
| population | 总体,人口 |
| population mean | 总体均数 |
| population rate | 总体率 |
| population variance | 总体方差 |
| positive correlation | 正相关 |
| positive skewness | 正偏态 |
| power of a test | 把握度,检验效能 |
| prevalence rate | 患病率 |
| probability | 概率,机率 |
| probability error | 偶然误差 |
| proportion | 比,比率 |
| prospective study | 前瞻研究 |
| prospective survey | 前瞻调查 |
| public health statistics | 卫生统计学 |
Q
| quality eontrol | 质量控制 |
| quartile | 四分位数 |
R
| random | 随机 |
| random digits | 随机数字 |
| random error | 随机误差 |
| random numbers table | 随机数目表 |
| random sample | 随机样本 |
| random sampling | 随机抽样 |
| random variable | 随机变量 |
| randomization | 随机化 |
| randomized blocks | 随机区组, 随机单位组 |
| randomized blocks analysis of variance | 随机单位组方差分析 |
| randomized blocks design | 随机单位组设计 |
| randomness | 随机性 |
| range | 极差、全距 |
| range of normal values | 正常值范围 |
| rank | 秩, 秩次, 等级 |
| rank correlation | 等级相关 |
| rank correlation coefficent | 等级相关系数 |
| rank-sum test | 秩和检验 |
| rank test | 秩 (和) 检验 |
| ranked data | 等级资料 |
| rate | 率 |
| ratio | 比 |
| recovery rate | 治愈率 |
| registration | 登记 |
| regression | 回归 |
| regression analysis | 回归分析 |
| regression coefficient | 回归系数 |
| regression eguation | 回归方程 |
| relative number | 相对数 |
| relative ratio | 比较相对数 |
| relative ratio with fixed base | 定基比 |
| remainder error | 剩余误差 |
| replication | 重复 |
| retrospective survey | 回顾调查 |
| Ridit analysis | 参照单位分析 |
| Ridit value | 参照单位值 |
S
| sample | 样本 |
| sample average | 样本均数 |
| sample size | 样本含量 |
| sampling | 抽样 |
| sampling error | 抽样误差 |
| sampling statistics | 样本统计量 |
| sampling survay | 抽样调查 |
| scaller diagram | 散点图 |
| schedule of survey | 调查表 |
| semi-logarithmic chart | 半对数线图 |
| semi-measursement data | 半计量资料 |
| semi-guartile range | 四分位数间距 |
| sensitivity | 灵敏度 |
| sex ratio | 性比例 |
| sign test | 符号检验 |
| significance | 显著性, 意义 |
| significance level | 显著性水平 |
| significance test | 显著性检验 |
| significant difference | 差别显著 |
| simple random sampling | 单纯随机抽样 |
| simple table | 简单表 |
| size of sample | 样本含量 |
| skewness | 偏态 |
| slope | 斜率 |
| sorting data | 整理资料 |
| sorting table | 整理表 |
| sources of variation | 变异来源 |
| square deviation | 方差 |
| standard deviation(SD) | 标准差 |
| standard error (SE) | 标准误 |
| standard error of estimate | 标准估计误差 |
| standard error of the mean | 均数的标准误 |
| standardization | 标准化 |
| standardized rate | 标化率 |
| standardized normal distribution | 标准正态分布 |
| statistic | 统计量 |
| statistics | 统计学 |
| statistical induction | 统计图 |
| statistical inference | 统计归纳 |
| statistical map | 统计推断 |
| statistical method | 统计地图 |
| statistical survey | 统计方法 |
| statistical table | 统计调查 |
| statistical test | 统计表 |
| statistical treatment | 统计检验 |
| stratified sampling | 统计处理 |
| stochastic variable | 分层抽样 |
| sum of cross products of | 随机变量 |
| deviation from mean | 离均差积和 |
| sum of ranks | 秩和 |
| sum of sguares of deviation from mean | 离均差平方和 |
| superior limit | 上限 |
| survival rate | 生存率 |
| symmetry | 对称(性) |
| systematic error | 系统误差 |
| systematic sampling | 机械抽样 |
T
| t-distribution | t 分布 |
| t-test | t 检验 |
| tabulation method | 划记法 |
| test of normality | 正态性检验 |
| test of one-sided | 单侧检验 |
| test of one-tailed | 单尾检验 |
| test of significance | 显著性检验 |
| test of two-sided | 双侧检验 |
| test of two-tailed | 双尾检验 |
| theoretical frequency | 理论频数 |
| theoretical number | 理论数 |
| treatment | 处理 |
| treatment factor | 处理因素 |
| treatment of date | 数据处理 |
| two-factor analysis of variance | 双因素方差分析 |
| two-sided test | 双侧检验 |
| two-tailed test | 双尾检验 |
| type I error | 第一类误差 |
| type II error | 第二类误差 |
| typical survey | 典型调查 |
U
| u test | u 检验 |
| universe | 总体, 全局 |
| ungrouped data | 未分组资料 |
| upper limit | 上限 |
V
| variable | 变量 |
| variance | 方差, 均方 |
| variance analysis | 方差分析 |
| variance ratio | 方差比 |
| variate | 变量 |
| variation coefficient | 变异系数 |
| velocity of development | 发展速度 |
| velocity of increase | 增长速度 |
W
| weight | 权数 |
| weighted mean | 加权均数 |
Z
| zero correlation | 零相关 |
计算公式索引
相对数
公式(3.1)
公式(3.2)
公式(3.3)![]()
χ2检验
公式(3.4)理论频数![]()
公式(3.5)χ2 基本公式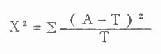
公式 (3.6)χ2 自由度 ν=(R-1)(C-1)
公式(3.7)χ2 校正的基本公式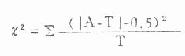
公式 (3.8) 四格表专用公式![]()
公式 (3.9) 四格表校正公式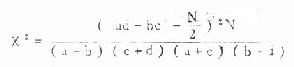
公式(3.10)2×k 表专用公式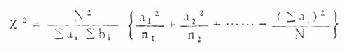
公式(3.11)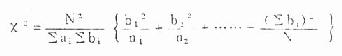
公式(3.12)R×C 表通用公式![]()
中位数
公式 (4.1) 当 n 为奇数时![]()
公式 (4.2) 当 n 为偶数时
公式 (4.3) 频数表上计算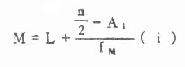
公式(4.4)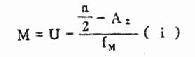
百分位数
公式 (4.5) 频数表上计算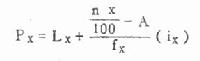
算术均数
公式(4.6) χ=(1/n)∑X
公式(4.7) χ=C+(1/n)(Xi-C)
公式(4.8) χa=Xa-1+(1/n)(Xa-Xa-1)
公式(4.9) χ=(1/n)∑fX
几何均数
公式(4.10)![]()
公式(4.11)![]()
四分位数间距
公式(4.12) Q=P75-P25
均差
公式(4.13)![]()
标准差
公式(4.14) 样本标准差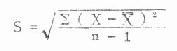
公式(4.15) 递推计算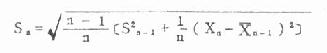
公式(4.16) 直接计算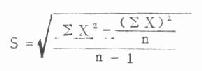
公式(4.17)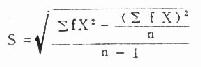
变异系数
公式(4.18) CV=S/X×100%,X>0
正态曲线
公式(5.1) 正态曲线方程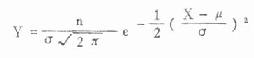
(5.2) 正态离差![]()
(5.3) 标准正态曲线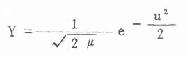
(5.4) 正常值范围 X±uαs
标准误
(6.1) 理论标准误![]()
(6.2) 样本均数的标准误![]()
(6.3) 率的标准误
(6.4)![]()
t 分布
(6.5)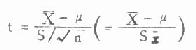
总体均数的估计
(6.6) 95% 可信区间 X-t0.05,νSχ<μ<x+t0.05,νSχ</x+t
(6.7) 99% 可信区间 X-t0.01,νSχ<μ<x+t0.01,νSχ</x+t
总体率的估计
(6.8) 95% 可信区间 P -1.96Sp<π<p+1.96sp<p< p=””></p+1.96sp<p<>
(6.9) 99% 可信区间 P -2.58Sp<π<p+2.58sp<p< p=””></p+2.58sp<p<>
t 检验
公式 (6.5) 样本均数与总体均数比较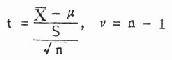
公式(7.1) 两样本均数比较的自由度 ν=n1+n2-2
公式(7.2) 合并方差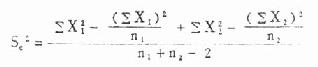
公式(7.3) 两均数相差的标准误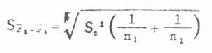
公式(7.4) t 检验![]()
u 检验
公式 (7.5) 两均数相关的标准误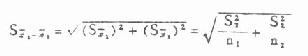
u 检验![]()
公式 (7.6) 两样本率比较![]()
![]()
公式(7.7)![]()
公式(6.4)![]()
正态性检验
公式(7.8) w 检验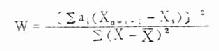
公式(7.9) 偏度系数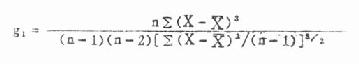
公式(7.10)![]()
公式(7.11) 峰度系数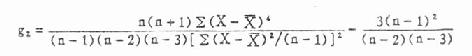
公式(7.12)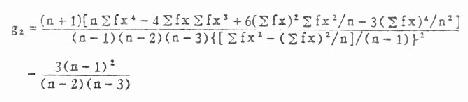
公式 (7.13) g1的抽样误差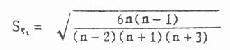
公式 (7.14) g2的抽样误差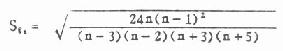
公式 (7.15) g1的 u 检验 u1=g1/Sg1
公式 (7.16) g2的 u 检验 u2=g2/Sg2
两方差齐性检验
公式(7.17) F=S12/S22,S1>S2
方差分析
公式(8.1) 总离均差平方和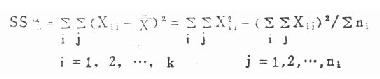
公式(8.2) 组间离均差平方和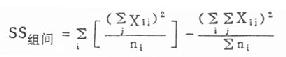
公式(8.3) 组内离均差平方和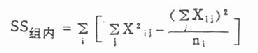
公式 (8.4) 总变异自由度 ν 总=N-1
公式(8.5)组间变异自由度 ν组间=k-1
公式 (8.6) 组内变异自由度 ν 组内=N-k
公式(8.7) F 检验 F = 组间均方 / 组内均方
多个均数间两两比较
公式(8.8) 最小显著相差 D α=t,νS![]() A-
A-![]() B
B
公式(8.9) 两均数的标准误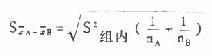
公式(8.10) 平均例数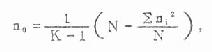 i=1,2,…,k
i=1,2,…,k
公式(8.11) 标准误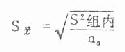
多个方差齐性检验
公式(8.12)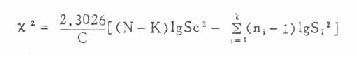
公式(8.13)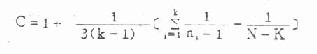
直线相关
公式(9.1) 直线相关系数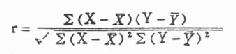
公式(9.2) 离均差积和![]()
公式(9.3) 相关系数 t 检验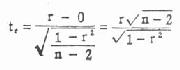
直线回归
公式(9.4) 直线回归方程 γ=a+bx
公式(9.5) 回归系数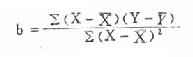
公式(9.6) 截距 a=γ-bχ
公式(9.7) 回归系数 t 检验![]()
公式(9.8) 回归系数的标准误![]()
公式(9.9) 标准估计误差![]()
公式(9.10) 估计误差平方和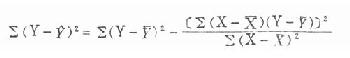
公式(9.11) 两回归系数相关的 t 检验![]()
公式(9.12) 两回归系数相差的标准误![]()
公式(9.13) 两回归系数的合并方差![]()
符号检验
公式(10.1) 成对资料比较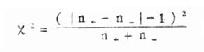 ,ν=1
,ν=1
公式(10.2) 秩号的中位数
公式(10.3) 两组符号检验![]() ,ν=1
,ν=1
公式(10.4) 两组符号检验![]() ,ν=组数-1
,ν=组数-1
秩和检验
公式(10.6) 成对资料比较
公式(10.6) 两组资料求较小 R'R'=n1(n1+n2+1)-R
公式(10.7)两组资料比较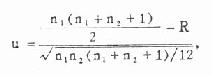
公式(10.8) 多组完全随机设计资料的比较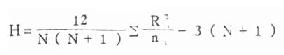
公式(10.9) 多组随机单位组设计资料的比较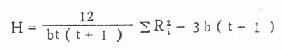
公式(10.10) 多组秩和的两两比较![]()
秩相关系数
公式(10.11)Spearman 秩相关系数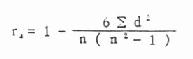
参照单位分析
公式(10.12) 平均 R 值![]()
公式(10.13)R 的标准误![]()
公式(10.14)R 的 95% 可信限![]()
样本含量的估计
公式(11.1) 两个率比较所需例数![]() ,1-β=0.5,α=0.05
,1-β=0.5,α=0.05
公式(11.2) 大样本成对资料比较均数所需例数 n=4S2/X2,1-β=0.5,α=0.05
公式(11.3) 小样本成对资料比较均数所需例数![]() ,1-β=0.5
,1-β=0.5